5.3 Кодування інформації

При передачі по каналах зв'язку завжди виникають помилки. Причини їх можуть бути різні, але результат видається один – дані спотворюються і не можуть бути використані на прийомній стороні для подальшого опрацювання. Як правило, можливість перекручування біта в потоку переданих даних на рівні фізичного каналу знаходиться в межах 10²...10^-6. У той же час із боку користувачів і багатьох прикладних процесів часто висовується вимога до можливості помилок у прийнятих даних не гірше
10^-6... 10^-12. Боротьба з виникаючими помилками ведеться на різних рівнях семирівневої моделі OSI (в основному на перших чотирьох). Для боротьби з виникаючими помилками відомо багато різноманітних способів.

В одному із способів на передавальній стороні передані дані кодуються одним із відомих кодів із виправленням помилок. На приймальній стороні, відповідно, проводиться декодування прийнятої інформації і виправлення виявлених помилок. Можливість застосовуваного коду з виправленням помилок залежить від числа надлишкових бітів, що генеруються кодером. Якщо внесена надмірність невелика, тобто існує небезпека того, що прийняті дані будуть містити незнайдені помилки, це може призвести до помилок у роботі прикладного процесу. Якщо ж використовувати код із високою виправлювальною здатністю, то це приводить до низької швидкості передачі даних. Таким чином, знання теорії завадостійкого кодування дозволяє визначити оптимальні параметри завадостійкого коду в залежності від поставленої задачі.

5.3.1 Завадостійке кодування

Завадостійкі коди – один з найбільш ефективних засобів забезпечення високої вірності як при зберіганні, так і при передачі дискретної інформації. Створено спеціальну теорію завадостійкості кодування, що швидко розвивається останнім часом.

К. Шеннон сформулював теорему для випадку передачі дискретної інформації з каналу із завадами, яка стверджує, що ймовірність помилкового декодування прийнятих сигналів може бути забезпечена як завгодно малою шляхом вибору відповідного способу кодування сигналів.

Під завадостійкими кодами розуміють коди, що дозволяють виявляти або виявляти і виправляти помилки, які виникають у результаті впливу завад.

Завадостійкість кодування забезпечується за рахунок введення надмірності в кодові комбінації, тобто за рахунок того, що не всі символи в кодових комбінаціях використовуються для передачі інформації.

Всі завадостійкі коди можна розділити на два основних класи: блокові і неперервні (рекуррентні або ланцюгові).

У блокових кодах кожному повідомленню (або елементу повідомлення) відповідає кодова комбінація (блок) із певної кількості сигналів. Блоки кодують і декодують окремо. Блокові коди можуть бути рівномірними, коли довжина кодових комбінацій n постійна, або нерівномірними, коли n мінлива.

Нерівномірні завадостійкі коди не одержали практичного застосування через складність їх технічної реалізації.

Як блокові, так і неперервні коди в залежності від методів внесення надмірності розділяються на роздільні і нероздільні. У роздільних кодах чітко розмежована роль окремих символів. Одні символи є інформаційними, інші є перевірними і служать для виявлення і виправлення помилок. Роздільні блокові коди називаються звичайно n-кодами, де n – довжина кодових комбінацій, k – число інформаційних символів у комбінаціях. Нероздільні коди не мають чіткого розділення кодової комбінації на інформаційні і перевірні символи. Цей клас кодів поки нечисленний. Роздільні блокові коди розділяються, у свою чергу, на несистематичні і систематичні.

Більшість відомих роздільних кодів складають систематичні коди. У цих кодів перевірні символи визначаються в результаті проведення лінійних операцій над певними інформаційними символами. Для випадку двійкових кодів кожний перевірний символ вибирається таким, щоб його сума за модулем два з певними інформаційними символами стала рівною нулю. Декодування зводиться до перевірки на парність певних груп символів. У результаті таких перевірок дається інформація про наявність помилок, а в разі потреби - про позицію символів, де є помилки.

Основні принципи завадостійкого кодування

Для з'ясування ідеї завадостійкого кодування розглянемо двійковий код, що знайшов на практиці найбільш широке застосування. Нагадаємо, що двійковий код – це код із основою m = 2. Кількість розрядів n у кодовій комбінації прийнято називати довжиною або значністю коду. Символи кожного розряду можуть приймати значення 0 і 1. Кількість одиниць у кодовій комбінації називають вагою кодової комбінації і позначають w.

Ступінь відмінності будь-яких двох кодових комбінацій даного коду характеризується так званою відстанню між кодами d. Вона виражається числом позицій або символів, у яких комбінації відрізняються одна від одної, і визначається як вага суми за модулем два цих кодових комбінацій.

Помилки, внаслідок впливу завад, виявляються в тому, що в однім або декількох розрядах кодової комбінації нулі переходять в одиниці і, навпаки, одиниці переходять у нулі. В результаті створюється нова - помилкова кодова комбінація.

Якщо помилки відбуваються тільки в одному розряді кодової комбінації, то їх називають однократними. При наявності помилок у двох, трьох і т. д. розрядах помилки називають дворазовими, триразовими і т. д.

Експериментальні дослідження каналів зв'язку показали, що помилки символів при передачі по каналу зв'язку, як правило, групуються в пачки різної тривалості. Під пачкою помилок розуміють ділянку послідовності, що починається і закінчується помилково прийнятими символами. Всередині пачки можуть бути і правильно прийняті елементи.

Для вказання місць у кодовій комбінації, де є перекручування символів, використовується вектор помилки е. Вектор помилки n-розрядного коду – це n-розрядна комбінація, одиниці в якій указують положення перекручених символів кодової комбінації.

Вага вектора помилки we характеризує кратність помилки. Сума за модулем два для перекрученої кодової комбінації і вектори помилки дають вихідну невикривлену комбінацію.

Як уже відзначалося, завадостійкість кодування забезпечується за рахунок внесення надмірності в кодові комбінації. Це значить, що з n символів кодової комбінації для передачі інформації використовується k < n символів. Отже, із загального числа N_o=2ⁿ можливих кодових комбінацій для передачі інформації використовується тільки N = 2^k комбінацій. Відповідно до цього вся множина N_o=2ⁿ можливих кодових комбінацій поділяється на дві групи. У першу групу входить множина N = 2^k дозволених комбінацій, друга група містить у собі множину (N_o - N) = 2ⁿ-2^k заборонених комбінацій.

Якщо на стороні приймання встановлено, що прийнята комбінація відноситься до групи дозволених, то вважається, що сигнал прийшов без перекручувань. В іншому випадку робиться висновок, що прийнята комбінація перекручена. Однак це справедливо лише для таких перешкод, коли усунута можливість переходу одних дозволених комбінацій в інші.

У загальному випадку кожна з N дозволених комбінацій може трансформуватися в будь-яку з N_o можливих комбінацій, тобто усього є N?No можливих варіантів передачі, із них:

N варіантів безпомилкової передачі;

N(N-1) варіантів переходу в інші дозволені комбінації;

N(No-N) варіантів переходу в заборонені комбінації.

Таким чином, не всі перекручування можуть бути виявлені. Частка помилкових комбінацій, що виявляються, складає

.

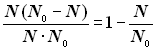Для використання даного коду як виправного множина заборонених кодових комбінацій розбивається на N підмножин, що не перетинаються. Кожна з підмножин ставиться у відповідність одній із дозволених комбінацій. Помилка виправляється в (N_o - N) випадках, рівних кількості заборонених комбінацій. Частка помилкових комбінацій, що виправляються, від загального числа помилкових комбінацій, що виявляються, складає

.

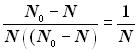Спосіб розбиття на підмножини залежить від того, які помилки повинні виправлятися даним кодом.

Нехай необхідно побудувати код, що виявляє всі помилки кратністю t і нижче.

Побудувати такий код – це означає із множини N_o можливих вибрати N дозволених комбінацій так, щоб будь-яка з них у сумі за модулем два з будь-яким вектором помилок із вагою W_l Ј t не дала б у результаті ніякої іншої дозволеної комбінації. Для цього необхідно, щоб найменша кодова відстань задовольняла умову

.

У загальному випадку для усунення помилок кратності s кодова відстань повинна задовольняти умову

.

Аналогічно міркуючи, можна встановити, що для виправлення всіх помилок кратності не більше s і одночасно виявлення всіх помилок кратності не більше t і (при tіs) кодова відстань повинна задовільняти умову

.

5.3.2 Коди із заданою виправною здатністю

Підвищення коригуючої здатності коду досягається при зберіганні n за рахунок зменшення множини N дозволених комбінацій (або зменшення кількості k інформаційних символів). Звичайно ж на практикці коди будуються в зворотному порядку: спочатку вибирається кількість інформаційних символів k, виходячи з об'єму алфавіту джерела, а потім забезпечується необхідна коригуюча спроможність коду за рахунок додавання надлишкових символів.

Нехай відомий об'єм алфавіту джерела N. Необхідна кількість інформаційних символів

.

Нехай також відомо повне число помилок Е, що необхідно виправити.

Завдання полягає в тому, щоб при заданих N і Е визначити значність коду n, що має необхідні коригуючі можливості.

Повне число помилкових комбінацій, які підлягають виправленню, дорівнює Е?2^k = Е?N. Тому, що кількість помилкових комбінацій дорівнює N_о – N, то код забезпечує виправлення не більше N_o – N комбінацій. Отже, необхідну умову для можливості виправлення помилок можна записати у вигляді

,

і отримаємо

,

або

.                (5.1)

Формула (5.1) виражає умову для вибору значності коду n. Розглянемо окремі випадки. Якщо є помилки різної кратності, то насамперед необхідно забезпечити усунення однократних помилок, ймовірність появи яких найбільша. Можлива кількість векторів однократних помилок

.

У цьому випадку залежність (5.1) набуде вигляду

.           (5.2)

При побудові коду доцільно користуватися табл. 5.1. Потрібно при цьому мати на увазі, що код повинен також задовільняти умову d_minі3.

Таблиця 5.1 – Виявлення значності коригуючого коду

Якщо необхідно забезпечити усунення всіх помилок кратності від 1 до l, то потрібно врахувати, що

кількість можливих однократних помилок E₁ = С¹_n,

кількість можливих дворазових помилок Е₂ = С²_n

кількість можливих l-кратних помилок E_l = С^l_n.

Загальна кількість помилок .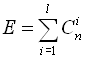

При цьому залежність (5.1) набуде вигляду

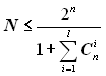. (5.3)

Умова (5.3) є нижньою оцінкою для довжини коригуючоого коду, тобто вона визначає необхідну мінімальну довжину коду n, що забезпечує виправлення помилок заданої кратності при відомому числі дозволених комбінацій N або числі інформаційних символів k = log₂ N.

Це ж умова є верхньою оцінкою для N або k, тобто визначає максимально можливе число дозволених комбінацій або інформаційних символів для коду довжини n, що забезпечує виправлення помилок заданої кратності.

Будь-який коригуючий код характеризується рядом показників: довжиною n, кількістю інформаційних символів k або надлишкових символів r = n - k, повним числом усіх можливих кодових комбінацій N_o = mⁿ (для двійкових кодів N = 2ⁿ), числом дозволених кодових комбінацій (потужністю коду) N, вагою кодової комбінації w, вагою вектора помилки w₁, кодовою відстанню d і ін.

Однак основним показником якості коригуючого коду є його спроможність забезпечити правильне прийняття кодових комбінацій при наявності перекручувань під впливом перешкод, тобто завадостійкість коду.

Коригуюча можливість коду забезпечується за рахунок надмірності, тобто подовження кодових комбінацій. При подовженні кодових комбінацій ускладнюється апаратура, збільшується час передачі й опрацювання інформації. Тому надмірність також є важливою характеристикою коду.

Для оцінки надмірності коду користуються поняттям коефіцієнта надмірності

,

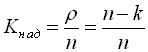де r – кількість надлишкових символів у кодовій комбінації.

Визначити коригуючу здатність коду, що має такі дозволені комбінації: 00000; 01110; 10101; 11011.

Розв’язання. Коригуюча здатність коду визначається мінімальною кодовою відстанню. Складемо матрицю відстаней між кодовими комбінаціями (табл. 5.2).

Таблиця 5.2 – Матриця відстаней

Як видно з матриці, мінімальна кодова відстань d_min=3. Отже, даний код здатний:

а) виявляти дворазові помилки;

б) усувати однократні помилки;

в) усувати і виявляти однократні помилки.

5.3.3 Систематичні коди

В наш час найбільш широкий клас коригуючих кодів складають систематичні коди. Ці коди відносяться до групи роздільних блокових кодів. Для систематичного коду сума за модулем для двох дозволених комбінацій також дає дозволену комбінацію.

В теорії кодування широко використовується матричне подання кодів. Всі дозволені кодові комбінації систематичного (n, k)-коду можна одержати, маючи k вихідних дозволених кодових комбінацій. Вихідні кодові комбінації повинні задовольняти такі умови:

1. У число вихідних комбінацій не повинна входити нульова.

2. Кодова відстань між будь-якими парами вихідних комбінацій повинна бути не менше d_min.

3. Кожна вихідна комбінація, як і будь-яка ненульова дозволена комбінація, повинна містити кількість одиниць не менше d_min.

4. Всі вихідні комбінації повинні бути лінійно незалежні, тобто, жодна з них не може бути отримана шляхом підсумовування інших.

Вихідні комбінації можуть бути отримані з матриці, що складається з k рядків і n стовпців:

.

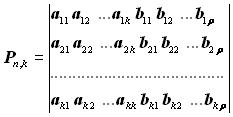Тут символи перших k стовпців є інформаційними й останні r стовпців кількість перевірними. Матрицю P_n,k називають породжувальною. Породжувальна матриця P_n,k може бути подана двома підматрицями – інформаційною U_k і перевірною Н_р:

,

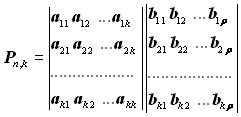де

; .

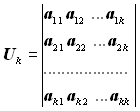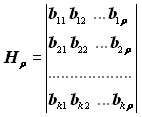Для побудови породжувальної матриці зручно інформаційну матрицю брати у вигляді квадратної одиничної матриці

.

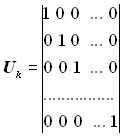При цьому перевірна підматриця Н_р повинна будуватися з дотриманням таких умов:

а) кількість одиниць у рядку повинна бути не менше d_min-1;

б) сума за модулем два двох будь-яких рядків повинна містити не менше d_min-2 одиниць.

Перевірні символи утворюються за рахунок лінійних операцій над інформаційними символами. Для кожної кодової комбінації повинно бути складено r незалежних сум за модулем два. Вибір інформаційних символів, що беруть участь у формуванні того або іншого перевірного символу, залежить від способу декодування коду. Дуже зручно перевірні суми складати за допомогою перевірної матриці Н, що будується в такий спосіб. Спочатку будується підматриця Н¹, що є транспонованою стосовно підматриці Нr:

.

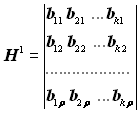Потім до неї справа приписується одинична матриця

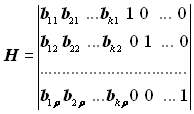.               (5.4)

Алгоритм визначення перевірних символів за інформаційними за допомогою матриці (5.4) такий. Позиції, які займаються одиницями в першому рядку підматриці Н¹, визначають інформаційні розряди, що повинні брати участь у формуванні першого перевірного розряду кодової комбінації. Позиції одиниць у другому рядку підматриці Н1 визначають інформаційні розряди, що беруть участь у формуванні другого перевірного розряду і т. д.

Перевірна матриця Н дуже зручна для визначення місця помилки в кодовій комбінації, а, отже, виправлення помилок. Перевірка кодових комбінацій при цьому виконується шляхом підсумовування за модулем два перевірних символів кодових комбінацій і перевірних символів, обчислених за прийнятими інформаційними. У результаті буде отримана сукупність контрольних рівностей, кожна з яких являє суму за модулем два одного з контрольних символів і певної кількості інформаційних.

Склад контрольних рівностей легко визначається з перевірної матриці Н. До складу першої контрольної рівності повинні входити символи, позиції яких зайняті одиницями в першому рядку матриці Н. До складу другої контрольної рівності повинні входити символи, позиції яких зайняті одиницями в другому рядку матриці Н, і т. д.

В результаті r таких перевірок буде отримане r-розрядне двійкове число (синдром), що буде рівне нулю при відсутності помилок і відмінним від нуля у випадку наявності помилок.

Якщо для виправлення однократних помилок у кодових комбінаціях одержати синдроми досить просто, то для виправлення дворазових, триразових і т. д. помилок, а також для виправлення пачок помилок побудова синдромів досить важка й у цих випадках звертаються звичайно за допомогою до ЕОМ.

Побудувати породжувальну матрицю систематичного коду, здатного виправляти одиничну помилку (s= 1) при передачі 16 повідомлень.

Розв’язання. Тому, що число дозволених кодових комбінацій N = 16, то число інформаційних розрядів у кодових комбінаціях

.

Отже, число рядків породжувальної матриці P_n,k повинно дорівнювати чотирьом.

Користуючись умовою (5.2) і табл. 5.1, знаходимо довжину коду n = 7. Отже, число стовпців матриці P_n,k дорівнює сім.

Оскільки число перевірних розрядів р = n - k = 3, то число стовпців перевірної підматриці Н_р дорівнює трьом. Кількість одиниць у кожному рядку підматриці Н_р повинна бути не менша d_{min - 1}. Для s=1 d_min = 2 s + 1= 3. Вибираємо для підматриці Н_р такі комбінації: 111, 110, 101, 011. Отже, перевірна підматриця може мати вигляд:

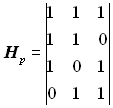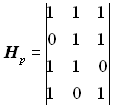, або , або .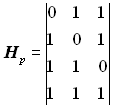

Інформаційну підматрицю U_k беремо у вигляді одиничної матриці з кількістю рядків і стовпців, рівною k = 4:

.

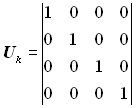Остаточний вид породжувальної матриці:

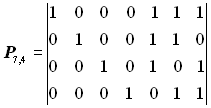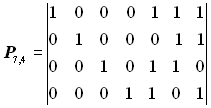, або , або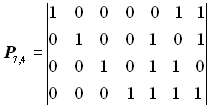

Побудувати перевірну матрицю H систематичного коду (7,4), утворююча матриця якого має вигляд

.

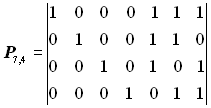Скласти рівняння для визначення перевірних символів.

Розв’язання. Знаходимо підматрицю H¹, що є транспонованою стосовно підматриці Н_р:

.

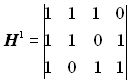Приписуючи до неї справа одиничну матрицю U_k, отримаємо перевірну матрицу

.

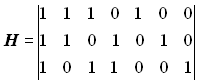Перевірні символи визначають шляхом підсумовування за модулем два певних інформаційних символів. Алгоритм визначення перевірних символів визначається підматрицею Н¹. Позиції, що займаються одиницями в першому рядку H¹ визначають інформаційні розряди, що повинні брати участь у формуванні першого перевірного розряду. Позиції одиниць у другому рядку визначають інформаційні розряди, що беруть участь у формуванні другого перевірного розряду. І, нарешті, позиції одиниць у третьому рядку визначають інформаційні розряди, що беруть участь у формуванні третього перевірного розряду. Отже, перевірні символи визначають рівностями

.

Побудувати комбінацію систематичного коду (7, 4) для випадку, коли проста ненадмірна комбінація має вигляд 0110.

Розв’язання. У даному випадку значення інформаційних символів такі: a₁=0; а₂= 1; a₃ = 1; a₄ = 0.

Тоді, використовуючи отримані в попередньому прикладі рівності для перевірних символів, визначимо:

Отже, повідомлення 0110, закодоване систематичним кодом (7, 4), прийме вигляд: 0110011.

Утворююча матриця коду (7, 4) має вигляд

.

Побудувати комбінацію систематичного коду (11, 7), що відповідає ненадмірній комбінації 1101001.

Розв’язання. Оскільки для одержання комбінації вигляду 1101001 необхідно скласти перший, другий, четвертий і сьомий рядки одиничної матриці U_k, для побудови перевірних розрядів варто скласти ці ж рядки підматриці H_р:

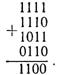
Таким чином, комбінація коду (11, 7) має вигляд 11010011100.