5.6 Кодування із стисненням інформації
Як відомо, застосування стиснення даних дозволяє більш ефективно використовувати ємність дискової пам'яті. Не менш корисне застосування стиснення при передача інформації в будь-яких системах зв'язку. У останньому випадку з'являється можливість передавати значно меншу (як правило, у декілька разів) кількість даних і, отже, необхідні значно менші ресурси пропускної спроможності каналів для передачі тієї ж самої інформації. Виграш може виражатися в скороченні часу занятості каналу і, відповідно, у значній економії орендної плати.
Науковою передумовою можливості стиснення даних виступає відома з теорії інформації теорема кодування для каналу без перешкод, опублікована наприкінці 40-х років у статті Клода Шеннона "Математична теорія зв'язку". Теорема підтверджує, що в каналі зв'язку без перешкод можна так перетворити послідовність символів джерела у послідовність символів коду, що середня довжина символів коду може бути як завгодно близька до ентропії джерела повідомлень Н(Х), обумовленої як:
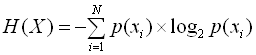
де р(хi) – можливість появи конкретного повідомлення хі із N можливих символів алфавіту джерела.
Число N називають об’ємом алфавіту джерела.
5.6.1 Код Шеннона-Фано
При передачі повідомлень, закодованих двійковим рівномірним кодом, не враховують статистичну структуру повідомлень, які незалежно від імовірності їх появи є кодовими комбінаціями однакової довжини, тобто кількість двійкових символів на одне постійне повідомлення. Такі коди мають надлишковість.
Найбільш ефективним способом зменшення надлишковості повідомлення є побудова оптимальних кодів, які мають мінімальну довжину кодових слів.
Враховуючи статистичні властивості джерела повідомлення, можна мінімізувати середнє число символів, які потрібні для вираження одного знаку повідомлення, що при відсутності шуму дозволяє зменшити час передачі або об’єм запам’ятовувального пристрою.
Ефективне кодування повідомлення для передачі їх по дискретному каналу без перешкод базується на теоремі Шеннона, яку можна сформулювати так: повідомлення джерела з ентропією 
завжди можна закодувати послідовностями символів з об’ємом алфавіту так, що середнє число символів на знак повідомлення 
буде якомога ближче до величини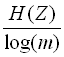 
, але менше за неї.
Для одержання оптимального коду, що має мінімальну довжину кодової комбінації, необхідно домагатися найменшої надмірності кожного з кодів слова, що у свою чергу повинні будуватися з рівноймовірнісних і взаємонезалежних символів. При цьому кожен кодовий елемент повинен приймати значення 0 чи 1 по можливості з рівними ймовірностями, а вибір наступного елемента повинен бути незалежним від попереднього. Алгоритм побудови такого коду вперше був запропонований К. Шенноном у 1948 році і трохи пізніше модифікований Р. Фано, у зв’язку з чим він одержав назву Шеннона-Фано.
Відповідно до алгоритму на початку процедури кодування всі символи алфавіту джерела заносяться в таблицю в порядку зменшення ймовірностей. На першому етапі кодування символи розбиваються на дві групи таким чином, щоб суми ймовірностей символів у кожній з них були по можливості однакові. Усім символам верхньої групи присвоюється елемент кодової комбінації 0, а всім нижнім – 1. На другому етапі кодування кожна з груп знову розбивається на дві рівноймовірнісні підгрупи. Другому елементу кодових комбінацій для верхньої підгрупи присвоюється значення 0, а нижній – 1. Процес кодування продовжується до тих пір, поки в кожній підгрупі не залишиться по одному символу. Аналогічно може бути побудований альтернативний варіант оптимального префіксного коду Шеннона-Фано, у якому в процесі кодування верхнім підгрупам символів присвоюється кодовий елемент 1, а нижнім – 0.
Цей код відрізняється від попереднього тим, що його кодові комбінації для відповідних символів будуть інверсними.
Розглянемо алгоритм Шеннона-Фано на прикладі кодування джерела, алфавіт якого складається з 8 символів 
, а імовірності появи символів у повідомленні дорівнюють від'ємним степеням двійки, тобто 
. Щоб ансамбль повідомлень джерела подав повну групу подій, у прикладі прийнято 
. Процедура розбивання символів на групи й підгрупи та утворення кодових слів показані у таблиці 5.4.
Середнє число бітів на символ при кодуванні в даному випадку кодом Шеннона-Фано дорівнює
,
а ентропія джерела
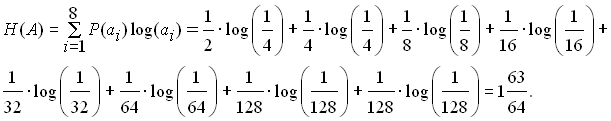
Таблиця 5.4 – Розбивання символів на групи й підгрупи
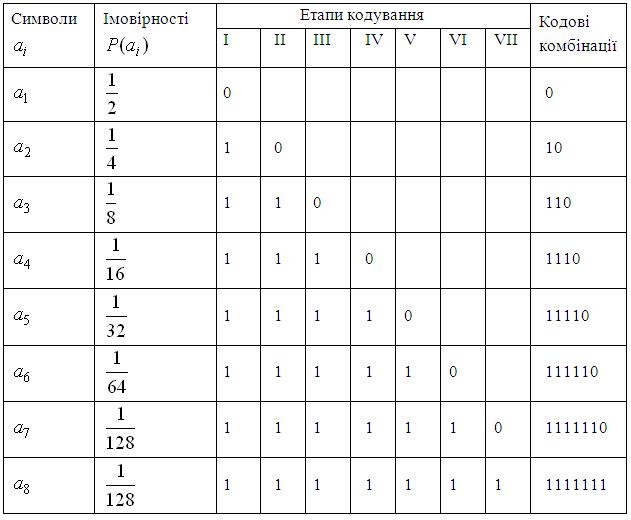
Таким чином, код Шеннона-Фано для заданого розподілу ймовірностей символів є оптимальним, оскільки середнє число бітів на символ у точності дорівнює ентропії джерела. При звичайному кодуванні для подання кожного символу необхідно 3 біти. Отже, коефіцієнт стиснення повідомлення за рахунок нерівномірного кодування Шеннона-Фано дорівнює
.
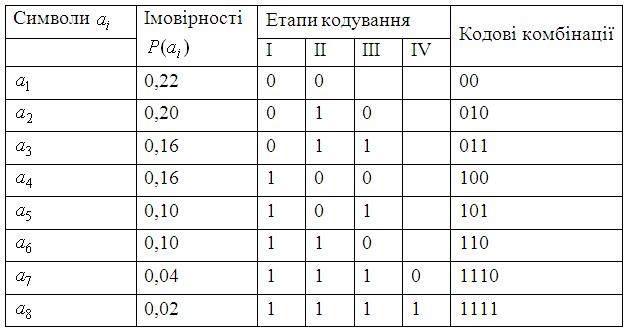
Приклад кодування за алгоритмом Шеннона-Фано для ансамбля символів з довільним розподілом імовірностей наведено у таблиці 5.5.
Таблиця 5.5 – Кодування за алгоритмом Шеннона-Фано
5.6.2 Код Хаффмена
Алгоритм Шеннона-Фано не завжди приводить до однозначної побудови коду. Це викликано тим, що при розбитті m символів джерела на підгрупи можна зробити більшими за імовірністю як верхню, так і нижню підгрупи. При різному розбитті на підгрупи середнє число бітів на символ може бути різним. Більш ефективний є алгоритм, запропонований Хаффменом у 1952 p., що дозволяє побудувати оптимальний код із найменшим для даного розподілу імовірностей середнім числом бітів на символ. Тобто
.
Для двійкового коду алгоритм Хаффмена зводиться до такого. Символи повідомлення упорядковуються за зменшенням ймовірностей і розташовуються в основний стовпець таблиці таким чином, що Р(аi) і P(aj) для усіх і<у (табл. 5.6).
Таблиця 5.6 – Алгоритм Хаффмена
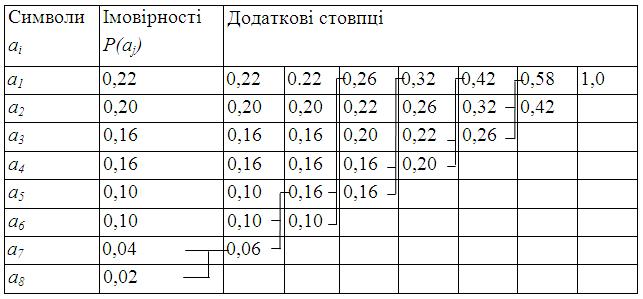
Два останніх символи поєднуються в один допоміжний, імовірність якого дорівнює сумарній імовірності складових його символів. Усі символи, що залишилися, разом з утвореним допоміжним символом, знову розташовуються за зменшенням імовірностей у додатковому стовпці. Два останніх елементи стовпця поєднуються в другий допоміжний символ, і утворюється наступний додатковий стовпець, у якому всі елементи, розташовані в порядку спадання ймовірностей. Процедура продовжується доти, поки не вийде єдиний допоміжний символ, що має імовірність, рівну одиниці. Для формування кодових комбінацій, що відповідають символам даного повідомлення, необхідно простежити шлях переходу символів по рядках і стовпцях таблиці. При побудові кодів Хаффмена найчастіше використовуються кодові дерева. З однієї сторони: це дозволяє більш наочно відобразити процедури кодування і декодування, а, з іншого боку – полегшити програмну реалізацію цих процедур (рис. 5.17).
Побудова дерева (рис. 5.17, а) починається з кореневого вузла, імовірність якого дорівнює 1. З кореня проводяться дві вітки, причому вітці з більшою імовірністю присвоюється значення (біт) 1, а з меншою імовірністю – 0. Знову утворені вузли можуть відображати одиничний чи допоміжний символи. В останньому випадку вузол є проміжним і з кожного з них, у свою чергу, знову проводяться по дві вітки. Таке послідовне розгалуження продовжується доти, поки не буде побудований вузол, що відповідає імовірності символу алфавіту (вузол листа). Рухаючись по кодовому дереву від кореня зверху вниз, можна записати для кожного символу відповідну йому кодову комбінацію (рис. 5.17, б).
а) |
б) |
Рисунок 5.17 – Кодове дерево (а) і таблиця коду Хаффмена (б)
Середнє число бітів на символ при такій побудові коду складає
Lcp = еP(ai)l(ai) = 0.22 ґ 2 ґ 0.2 ґ 2 ґ 0.16 ґ 3 ґ 0.16 ґ 3 ґ 0.1ґ
ґ 3 ґ 4 ґ 0.04 ґ 5 = 2.8 біта
Ентропія джерела повідомлення дорівнює:
H(A)=-еP(ai)logP(ai)= - (0,221og0,22 + 0,21og0,2 + 0,16log0,16 + +0,16log0,16 + 0,llog0,l + 0,1log0,1 + 0,041og0,04 + 0,02log0,02 = 2,754 біта
Як видно з розглянутого прикладу, середня довжина кодової комбінації й ентропія джерела практично збігаються, тобто отриманий код є оптимальним.
Алгоритм є двопрохідним, тому що при його реалізації потрібно двічі переглядати кодоване повідомлення. При першому проході обчислюються імовірності (частоти) появи символів у повідомленні і будується хаффменівське дерево.
При другому проході здійснюється кодування символів, що надійшли від джерела. У цьому випадку визначається значення віток дерева при русі від листка, що відповідає кодованому символу, до кореня. Очевидно, що для прискорення процедури декодування біти кодової комбінації на вихід кодера повинні видаватися, починаючи зі старшого розряду, тобто з вітки дерева, що виходить від кореня. На практиці замість імовірностей символів використовують абсолютні значення кількості (вага) символів у переданому повідомленні, тому що кількість символів пропорційна імовірності їхньої появи. Для однозначного декодування таблиця імовірностей символів повідомляється декодеру.
