5.6.3 Арифметичне кодування

При арифметичному стисненні повідомлень алфавіту джерела ставиться у відповідність числовий, відкритий справа, інтервал [0,1), а кожен символ алфавіту зіставляється з різними ділянками цієї числової осі. Ширина інтервалу (діапазон) кожної ділянки залежить від імовірності (частоти) появи символу в повідомленні.

Розглянемо, як приклад, алфавіт, що складається із шести символів A, B, С, D, E, ! з імовірностями появи відповідно 0,1; 0,1; 0,3; 0,2; 0,2 та 0,1. Тоді інтервал [0,1) може бути розділений на ділянки таким чином:

A: [0, 0,1), B: [0,1, 0,2), С: [0,2, 0,5),

D: [0,5, 0,7), E: [0,7, 0,9), !: [0,9, 1,0).

Розподіл числової осі ілюструється рис. 5.18. Як видно з прикладу, поділ одиничного інтервалу зручно здійснюється підсумовуванням імовірності кожного з границею попереднього.

Рисунок 5.18 – Розподіл відрізків числової осі між символами при арифметичному кодуванні

У процесі стиснення рядок текстового повідомлення подається двома дробовими числами, що відображають деякий інтервал числової осі [0, 1). До початку кодування допустимою областю для повідомлення є інтервал [0, 1). При надходженні від джерела першого символу йому виділяється інтервал, що відповідає розташуванню цього символу на осі [0, 1) відповідно до імовірності появи його в повідомленні. Надходження наступного символу звужує виділений інтервал. При цьому границі нового інтервалу визначаються числовим діапазоном, що відповідає черговому символу, тобто ширина діапазону пропорційна імовірності символу. З приходом наступного символу відбувається подальше звуження інтервалу. Таким чином, із збільшенням довжини рядка, що кодується, відбувається постійне звуження інтервалу. Теоретично його можна звужувати як завгодно довго, а на практиці цей інтервал обмежується технічними можливостями кодувальних пристроїв (розрядністю слова).

Число бітів, необхідне для подання інтервалу шириною s, дорівнює . Основа логарифму тут і в наступних виразах дорівнює 2. Ширина s останнього інтервалу рядка повідомлення, що складається з символів визначається добутком ймовірностей символів повідомлення

.

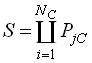В зв’язку з цим можна записати, що

,

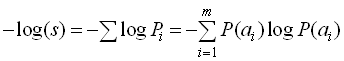де m – кількість різних символів повідомлення .

Таким чином, число бітів, затрачуване на кодування повідомлення, при арифметичному кодуванні в точності дорівнює ентропії джерела.

Розглянемо процедуру арифметичного стиснення на прикладі кодування рядка повідомлення (CADA!).

Тут символ ! є ознакою закінчення рядка. Імовірності появи символів і відповідні їм числові діапазони візьмемо з попереднього прикладу. Початковий числовий діапазон, який виділяється для кодера, дорівнює одиниці [0,1). Після надходження від джерела першого символу С числовий інтервал звужується до величини [0,2, 0,3). З приходом наступної букви А границі діапазону стають рівними [0,2, 0,23).

Процедура кодування наочно ілюструється на рис. 5.19. Вертикальні лінії відображають початкову числову вісь [0, 1) і її наступні ділянки в збільшеному розмірі (промасштабовані на одиничну вісь) на різних етапах кодування. Який би не був довгий рядок, кінцевий діапазон завжди буде розташований в інтервалі першого кодованого символу. Підрахунок інтервалів здійснюється за рекурентною формулою

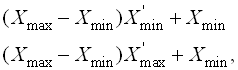
де – нижня і верхня границі для попередньої ітерації;

– границі інтервалу нового символу.

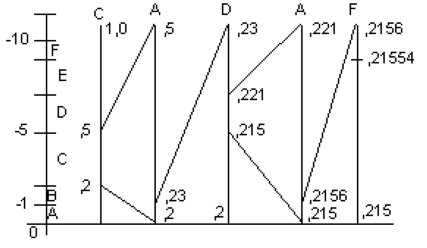
Рисунок 5.19 – Ілюстрація процедури арифметичного кодування

Межі інтервалів для всіх етапів кодування наведені в табл.5.7. Таким чином, числовий інтервал з межами [0,21554-0,2156) відображає рядок повідомлення CADA! Для кодування цього рядка може бути використано будь-яке число з отриманого діапазону. Нехай таким числом є нижня межа інтервалу, тобто X = = 0,21554.

Таблиця 5.7 – Результати арифметичного кодування

У процесі декодування здійснюється зворотна процедура ототожнення прийнятого числа (інтервалу) із закодованим рядком символів. Очевидно, що на приймальній стороні повинні бути відомі ймовірності декодованих символів і відповідні їм інтервали числової осі [0,1). Нехай на вхід декодера надійшло число X = 0,21554. Оскільки воно перебуває в діапазоні 0,2 - 0,5, тобто 0,2X<0,5, то на вихід декомпресора видається символ С. Потім декодер визначає, в яку відносну частку відрізка [0,2 – 0,5) потрапляє число 0,21554, для цього він робить обчислення за формулою

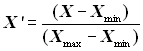, (5.7)

де – відносне значення числа X на черговій ділянці числової осі.

У нашому випадку = (0.21554 - 0,2) / 0,3 = = 0,0518. Оскыльки 0 < X < 0,1, то на вихід декомпресора надходить символ А. Неважко помітити, що процедура визначення вихідного символу рекурентна, при якій після знаходження першого діапазону для заданого числа X на одиничній числовій осі визначається відносна частка (діапазон) цієї частини відрізка, куди потрапляє декодоване повідомлення.

Обчислення на наступному кроці проводиться за формулою (5.7) з припущенням, що X= де  – відносне значення числа, знайденого в попередній ітерації. Нові значення X_min і X_max визначаються межами інтервалу, ідентифікованого на попередній ітерації. На цьому кроці X = 0,0518, X_min = 0, X_max = 0,1, а = 0,0518/0,1 = 0,518. Нове відповідає символу D, оскільки 0,5 < < 0,7.

Далі, вважаючи, , , , знайдемо аналогічно , що відповідає символу А. Оскільки на наступній ітерації , то декодер виводить символ !.

У зв'язку з тим, що символ ! є ознакою закінчення рядка повідомлення, то декодування на цьому закінчується.

Провести компресію і декомпресію повідомлення ”ІНФОРМАЦІЯ”, використовуючи метод арифметичного кодування.

Визначимо ймовірності появи символів у заданому повідомленні і розподілимо символи на одиничному відрізку (табл. 5.8). На підставі алгоритму кодування розрахуємо нижні і верхні границі кодового числа, що відображає стисле повідомлення, в залежності від кількості закодованих символів.

Таблиця 5.8 – Розподіл символів на одиничному відрізку

Дані розрахунку зведемо в табл. 5.9. Як кодове число, що відображає стисле повідомлення, приймемо нижню межу цього числа: 0.1951261656.

Таблиця 5.9 – Дані розрахунку

Використовуючи алгоритм декодування, зробимо процедуру декомпресії, етапи якої наведено в табл. 5.10.

Таблиця 5.10 – Результати процедури декомпресії