5.6.4 Динамічне кодування методом Хаффмена
Класичний метод кодування Хаффмена визначає від початку перетворення вірогідності появи символів на виході джерела інформації, причому символи впорядковується за спаданням вірогідностей їх виникнення. Для впорядкованого списку складається кодова таблиця, у якій довжина вихідної комбінації визначається вірогідністю вихідного символу. Природно, що на передавальній та приймальній сторонах повинні бути відомі таблиці (кодові дерева) для кожного повідомлення, що стискається. Цей метод має два вагомих недоліки. Перший полягає в тому, що для його реалізації потрібно два проходи кодованого масиву. При першому перегляді обчислюються імовірності появи кожного знака в повідомленні і складається таблиця коду Хаффмена. На наступному етапі здійснюється кодування на підставі статичної структури дерева Хаффмена і передача символів у стиснутому вигляді. Таким чином, виграш, отриманий за рахунок стискання даних, може помітно знижуватись, особливо при передачі щодо короткого повідомлення, у зв’язку з необхідністю передавати декодеру додаткову інформацію про кодове дерево. Другий недолік – наявність затримки від моменту надходження даних від джерела до видачі відповідних кодових комбінацій, що обмежує використання нерівномірного кодування в синхронних мережах передачі інформації, а також у системах, що функціонують у реальному часі.
На початку 70-х років були розроблені однопрохідні методи стискання інформації, основані на класичній процедурі кодування Хаффмена. Усі ці методи незначно відрізняються один від одного і їхня суть полягає в тому, що передавач будує дерево Хаффмена в темпі надходження даних від джерела, тобто “на ходу”. У процесі кодування відбувається “навчання” кодера на основі статичних характеристик джерела повідомлень, у ході якого обчислюється оцінка вихідних імовірностей повідомлення і виробляється відповідна модифікація кодового дерева, цей процес отримав назву динамічного кодування Хаффмена. Очевидно, що для правильного відновлення стиснутих даних, декодер також повинен постійно “вчитися” поряд із кодером, здійснюючи синхронну зміну кодової таблиці на приймальній стороні. Для забезпечення синхронності процесів кодування і декодування кодер видає символ у нестиснутому вигляді, якщо він уперше з’явився на виході джерела, і визначає його на кодовому дереві. З повторною появою символу на вході кодера він передається нерівномірною кодовою комбінацією, обумовленою позицією символу на поточному кодовому дереві. Кодер корегує дерево Хаффмена збільшенням частоти передачі символів, що уже введені в дерево, чи нарощує дерево, додаючи в нього нові вузли.
Найважливішою умовою, якої потрібно дотримуватись при модифікації кодового дерева, є збереження властивостей хаффменівського дерева. Для формулювання цих властивостей звернемося ще раз до алгоритму побудови оптимального коду Хаффмена. При статичному кодуванні символи розміщуються в списку в порядку спадання ваг (ймовірностей). Потім проводиться об’єднання двох вузлів найменшої ваги 
і заміна їх внутрішнім вузлом з вагою, рівною сумі вихідних ваг 
. Знову утворений вузол розміщується в списку таким чином, щоб не порушувався порядок розташування вузлів за вагами. Цей процес повторюється доти, поки в списку не залишиться один, так званий кореневий вузол.
Розглянемо приклади побудови дерев оптимального коду Хаффмена для букв алфавіту від А до H. Ваги цих символів відповідно мають: A=18; B=10; C=2; D=2; E=1; F=1; G=1; H=1. Проаналізуємо їх властивості. Як видно з рисунків, вузли дерева розташовані в порядку зростання їхніх ваг при обході дерева від крайнього нижнього вузла до кореня зліва, направо і знизу вверх. У зв’язку з тим, що вузли з вагами поєднуються парно, то на одному рівні не може бути менше двох вузлів, причому пари вузлів є дочірні в загальному батьківському вузлі, вага якого дорівнює сумі ваг дочірніх вузлів. Неважко переконатися, якщо при побудові дерева припустити, що дочірній вузол із великою вагою з’єднаний нульовою віткою, а з меншою вагою – одиничною, то хаффменівське дерево залишається упорядкованим за зростанням ваг при русі від нижнього вузла до кореня по рівнях справа наліво.
При побудові кодових дерев і їхньої модифікації проводиться нумерація вузлів із першого до 
-го в порядку збільшення їхніх ваг. Перший номер присвоюється вузлу з мінімальною вагою. Тут 
- число символів алфавіту джерела. На рис. 5.20 показано дерево Хаффмена, побудовене для вищенаведеного прикладу 18А, 10В, 3С, 2D, 1E, 1F, 1G, 1H, відповідно. Зробимо нумерацію вузлів дерева, починаючи з листка з мінімальною вагою (нижнім крайнім лівим вузлом). Як видно з рисунка, властивості хаффменівського дерева, побудованого для статичного коду, зберігаються, хоча воно й набуло іншу конфігурацію.
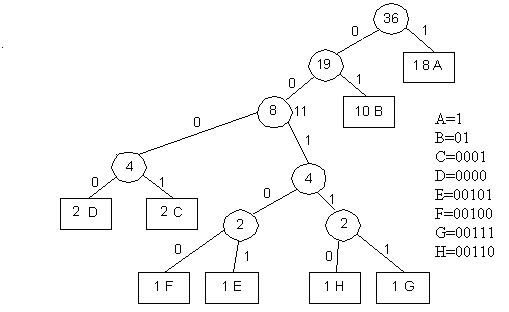
Рисунок 5.20 – Дерево Хаффмена для повідомлення, що складається зі символів A; B; C; D; E; F; G; H
При динамічному кодуванні Хаффмена після одержання від джерела наступного символу (наприклад, “С”) повинен збільшитись на 1 вагу відповідного йому листка (рис. 5.21). При цьому ваги усіх вузлів на шляху від листка із символом С до кореня збільшиться на 1. Але це приведе до порушення порядку розташування вузлів за вагами, властивому оптимальному кодовому дереву. Тому при одержанні чергового символу від джерела необхідно здійснити модифікацію кодового дерева, щоб воно залишалося оптимальним, так званим хаффменівським деревом.
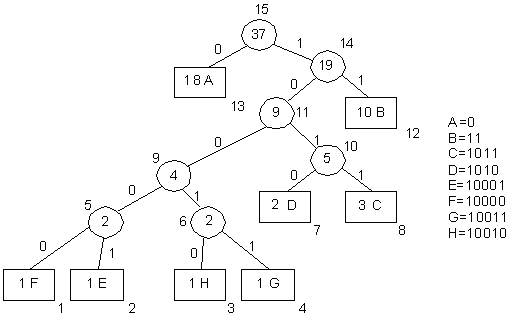
Рисунок 5.21 – Модифіковане дерево Хаффмена після надходження чергового символу “С”
Таким чином, на підставі аналізу властивостей оптимальних кодових дерев можна зробити висновок, що кодове дерево, яке має зовнішніх вузлів, є хаффменівським, якщо воно має такі властивості:
а) зовнішні вузли (листки) хаффменівського кодового дерева мають вагу 
; кожен внутрішній (батьківський) вузол має підпорядковані (дочірні) вузли, а його вага дорівнює сумі підпорядкованих (дочірніх) ваг;
б) на кожному рівні дерева (за винятком кореневого) повинно бути не менше однієї пари вузлів, що мають загальний батьківський вузол;
в) усі вузли нумеруються в зростаючому порядку таким чином, що вузли з номерами (2j - 1) та 2j є вузлами одного рівня для l < j < m - l, а їх загальний батьківський вузол має більш високий рівень;
г) нумерація вузлів відповідає тому порядку, у якому вузли поєднуються відповідно до статичного алгоритму Хаффмена.
5.6.5 Динамічне кодування методом FGK
Уперше алгоритм синтезу динамічного коду Хаффмена був запропонований Н. Феллером у 1973 році, а потім модифікований Р. Галлагером і Д. Батогом. У зв’язку з цим він одержав назву “алгоритм FGK”.
Введемо деякі позначення, що будуть використовуватись при аналізі й синтезі динамічного кодового дерева Хаффмена за алгоритмом FGK:
– розмір алфавіту джерела повідомлень;
символ алфавіту;
– перші 
символів у повідомленні;
– число символів у повідомленні, оброблених до поточного моменту часу;
– k-й символ у повідомленні;
К – кількість різних символів, оброблених на даний момент часу;
– число (вага) символів 
, що надійшли на момент обробки повідомлення;
– відстань від кореня дерева до -го листка.
Суть алгоритму синтезу динамічного кодового дерева Хаффмена полягає в процедурі обчислення листків і побудові бінарного дерева з мінімальною вагою шляху 
. Процедуру можна умовно розбити на два етапи, хоча при реалізації алгоритму вони можуть легко бути об’єднані в один. На першому етапі дерево Хаффмена, побудоване після обробки повідомлення 
, перетвориться в інше, еквівалентне вихідному, яке потім простим збільшенням ваг може бути перетворене в хаффменівське дерево для 
.
Перший етап починається після одержання від джерела символу 
із присвоєння статусу поточного вузла листка . Потім проходить обмін поточного вузла (включаючи утворене ним піддерево), із вузлом, що має найбільший порядковий номер та вагу. Після цього як новий поточний вузол ініціюється батьківський вузол останнього поточного вузла. Обмін вузлами в разі потреби багаторазово повторюється, поки не буде досягнутий корінь дерева. Неважко переконатися, що максимальна кількість перестановок, які можуть знадобитися при модифікації кодового дерева, дорівнює висоті дерева 
.
На другому етапі формується листок дерева, що відповідає оброблюваному символу і наступні проміжні вузли, розташовані на шляху руху від листка до кореня дерева.
Оригінальний спосіб був запропонований Д. Кнутом. Його суть полягає в тому, що усі символи використовуваного алфавіту, які ще не з’явилися на виході джерела, відмічаються на дереві нульовим вузлом. Тому, коли символ, що підлягає стисненню, генерується вперше, кодер “відзначає” його, виробляючи префіксну комбінацію. Слідом за нею на вихід надходить код нестиснутого символу. Як префіксна комбінація використовується код, що відповідає листку нульової ваги. Для кодування символів, що надійшли від джерела вперше, використовується не 8-ми розрядна комбінація ASCII-коду, а мінімальний префіксний код, побудований на підставі таких міркувань: якщо є повідомлення, що складається із символів 
, то число можна подати у вигляді цілого степеня двійки і цілого числа
,
де 
.
Тоді 
-й символ кодується 
-ю бітовою комбінацією числа 
, якщо 
.
У протилежному випадку – 
-ю бітовою комбінацією числа 
. Наприклад, якщо 
, то 
, а символи джерела будуть відображатися комбінаціями:
.
Неважко помітити, що отриманий код має властивість префікса. Цей код є оптимальним, якщо символи мають однакову імовірність.
5.6.6 Динамічне кодування методом Віттера
Подальше удосконалення алгоритму динамічного кодування даних нерівномірними кодами FGK було запропоноване Д. Віттером. Цей алгоритм одержав назву алгоритму V. При пошуку шляхів оптимізації процедури кодування даних кодом Хаффмена автор виходив із того, що в новому алгоритмі число обмінів вузлів у процесі модифікації кодового дерева повинна обмежуватись деяким малим числом (у кращому випадку одиницею), а динамічне хаффменівське дерево повинна будуватися таким чином, щоб мінімізувати не тільки сумарну довжину зовнішнього шляху 
, але і величину 
. Мінімізація висоти дерева 
дозволить запобігати утворенню довгих кодових комбінацій при кодуванні чергового символу в повідомленні. Віттеру значною мірою вдалося вирішити поставлену задачу. Розроблений ним алгоритм має в порівнянні з алгоритмом FGK такі дві переваги.
1. Кількість обмінів вузлами, при яких поточний вузол переміщується вгору по кодовому дереві в процесі його модифікації, обмежується одиницею. В алгоритмі FGK верхня границя числа обмінів складає 
, де - довжина кодового слова для 
-го символу до початку процедури модифікації.
2. Алгоритм V мінімізує довжину зовнішнього шляху дерева і гарантує дерево мінімальної висоти за умови мінімізації сумарної довжини зовнішнього шляху дерева .
Суть удосконалення алгоритму V полягає у введені нової системи нумерації вузлів кодового дерева, що одержала назву неявної нумерації (Implicit numbering).
При неявній нумерації вузли хаффменівського дерева нумеруються в порядку збільшення по рівнях зліва направо і знизу вверх, тобто, вузли більш низького рівня мають номери менші ніж вузли наступного рівня. Найважливішою особливістю неявної нумерації є дотримання необхідної умови побудови дерева.
Для кожної ваги W всі зовнішні вузли (листи) дерева з вагою W повинні передавати всім внутрішнім вузлам ваги W.
Неважко помітити, що ця умова є однією з відмінних рис неявної нумерації у порівнянні з іншими алгоритмами.
Тому, якщо передача продовжиться із символів d, c, g, e, f чи з ще не використаних символів, то формовані кодові слова в алгоритмі V будуть коротші, ніж у FGK, тобто стратегія мінімізації зовнішнього шляху й висоти дерева оптимальна при припущенні, що будь-який символ, який з’являється, рівноймовірний.
Другою відмінною рисою алгоритму V є введення поняття блока еквівалентних вузлів. При цьому вузли 
еквівалентні тільки тоді, якщо вони мають однакову вагу і обоє є або внутрішніми, або зовнішніми вузлами. Вузол блока, що має (при неявній нумерації) найвищий номер, називається лідером блока. Блоки впорядковуються за збільшенням ваги, причому блок листків ваги W повинен дорівнювати блоку внутрішніх вузлів однієї і тієї ж самої ваги.
Третя відмінна риса алгоритму V полягає в способі модифікації дерева після одержання чергового символу. Головною операцією алгоритму за підтримкою умови неявної нумерації (*) є ковзання й збільшення (Slide and Increment). Суть цієї операції полягає в тому, що вузол, оголошений поточним, обмінюється з лідером свого блока і потім зісковзує в напрямку кореня дерева по сусідньому блоці, що безпосередньо примикає до блоку поточного вузла. Ковзання продовжується доти, поки поточний вузол не пройде весь блок і буде установлений у початок цього блока. Потім здійснюється збільшення ваги поточного вузла і новим поточним вузлом призначається батько старого поточного вузла. Операція ковзання із збільшенням продовжується до досягнення кореня дерева. При цьому вибір батьківського вузла залежить від того чи був поточний вузол листком, чи внутрішнім вузлом. Якщо поточний вузол був листком, то новим поточним вузлом стає батько, із яким виявився зв’язаний поточний вузол після завершення ковзання. А у випадку, якщо поточним вузлом був внутрішній вузол, то новим поточним вузлом призначається його батьківський вузол, із яким був пов’язаний поточний до початку ковзання.
