Вінницький державний технічний університет містить море(!) аналітичної інформації

Ієрархічна модель даних

Деревоподібна (ієрархічна) структура (рис. 3.1) , або дерево, - це зв'язний неорієнтований граф, що не містить циклів, тобто петель з замкнутих шляхів.

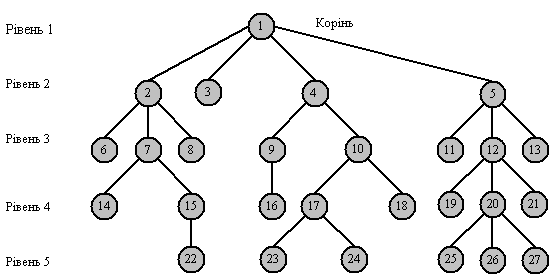
Як правило, при роботі з деревом виділяють яку-небудь конкретну верхівку (початок), визначають її як коріння дерева і розглядають особливо - в цю верхівку не заходить жодне ребро. В цьому випадку дерево стає орієнтованим. Орієнтація на кореневому дереві визначається або від коріння, або до коріння.

Кореневе дерево можна визначити наступним чином:

1) є єдиний особливий вузол , який називається корінням, в який не заходить жодне ребро;

2) в всі інші вузли заходить тільки одне ребро, а виходить довільна (0, 1, 2,..., п) кількість ребер;

3) не існує циклів.

В програмуванні використовується інше визначення дерева, яке дозволяє розглядати дерево як рекурсивну структуру.

Рекурсивне дерево визначається як кінцева множина Т, яка складається з одного або більш вузлів, таких, що:

1) існує один спеціально виділений вузол, який називається корінням дерева;

2) інші вузли розбиті на m>0 неперетинаючихся підмножини T1,T2, …, Tm, кожна з яких в свою чергу є деревом. T1,T2, …, Tm, називаються піддеревами.

З визначення слідує, що будь-який вузол дерева є корінням деякого піддерева, що міститься в повному дереві. Число піддерев вузла називають ступенем вузла. Вузол називається кінцевим, якщо він має нульову степінь. Інколи кінцеві вузли називають листками, а ребра -гілками . Кожний вузол, крім кореневого , зв'язаний з одним вузлом на більш високому рівні ієрархії і називається вихідним. Кожний вузол може бути зв'язаний з одним або декількома вузлами на більш низькому рівні і називається породженим.

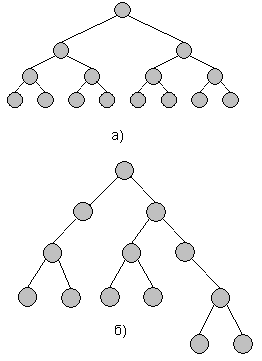
Якщо кожний вузол має однакову кількість гілок, причому процес включення нових гілок іде зверху вниз , а на кожному рівні дерева - зліва направо, то таке дерево називається залансованим (рис. 3.2,a). Для збалансованих дерев фізична організація даних суттєво спрощується. До особливої категорії дерев відносять двійкове (бінарне) дерево. Це дерево має не більш як дві гілки, які виходять з одного вузла. Двійкові дерева можуть бути як збалансованими, так і незбалансованими (рис. 3.2,б).

Прикладом простого ієрархічного представлення може служити адміністративна структура вищого учбового закладу (рис. 3.3.) : університет - відділення - факультет - група (студентська).

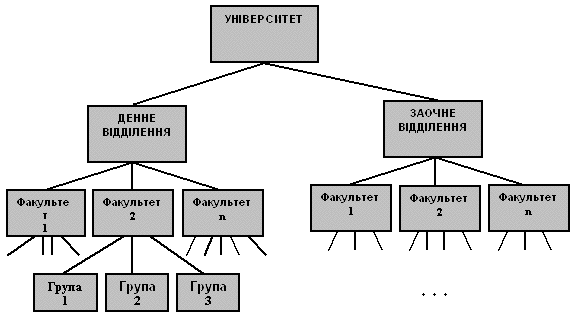
Рисунок 3.3 - Ієрархічне представлення адміністративної структура вищого учбового закладу

Пошук даних у ієрархічній структурі виконується завжди по одній із гілок, починаючи з кореневого елемента, тобто повинний бути зазначений повний шлях руху по гілкам. Так, для пошуку і вибірки одного або декількох екземплярів запису типу СТУДЕНТ (див.рис. 3.4 ) необхідно вказати кореневий елемент ФАКУЛЬТЕТ і елементи КУРС, ГРУПА. У операційній системі MS-DOS для пошуку файла використовується такий же принцип - вказуються послідовно ім'я диска, ім'я каталогу, ім'я підкаталогів, ім'я файла.

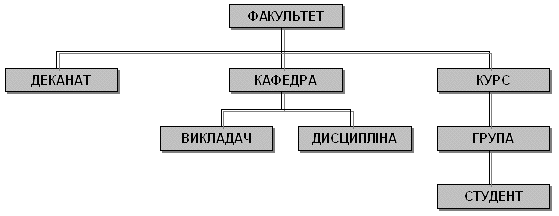
Рисунок 3.4 - Приклад ієрархічної структури

На рис. 3.5 приведений приклад типу набору, представленого у виді діаграми Бахмана. Діаграму назвали по імені вченого, який вперше їх застосував для опису відношень між даними при розробці СКБД IDS.

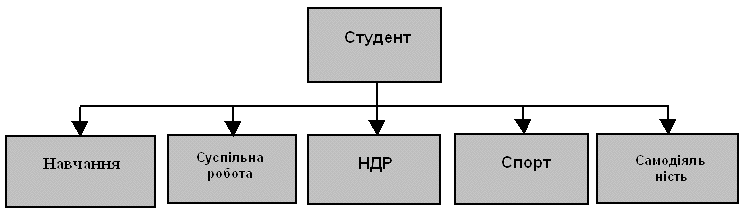
Рисунок 3.5 - Приклад типу набору у виді діаграми Бахмана

На такій діаграмі кожний прямокутник представляє собою тип запису , а стрілка - відношення "один до багатьох" між типами запису.. У прикладі на рис. 3.5 тип запису СТУДЕНТ є записом-власником, а типи записів НАВЧАННЯ, СУСПІЛЬНА РАБОТА, НДР, СПОРТ і САМОДІЯЛЬНІСТЬ -записами - членами. Тип набору названий ім'ям СУОНСС по перших літерах імен усіх типів запису, що беруть участь у наборі (наборові можна було надати і будь-яке інше ім'я). У цілому приведений тип набору призначений для того, щоб відобразити зв'язок між загальними даними про студента, що знаходяться в типі запису СТУДЕНТ, і даними, що характеризують різні сторони діяльності студента у вузі. При традиційному підході всі ці данні можна було б помістити в один загальний запис. Оскільки не кожний студент бере участь, наприклад, у спорті або самодіяльності, то прийшлося б вибрати запис з змінною довжиною або запис із фіксованою довжиною, причому в останньому випадку частина пам'яті витрачалася б даремно. Ієрархічна структура усуває виникаючі при цьому складнощі , тому що в будь-якому екземплярі типу набору з записом-власником можна асоціювати стільки записів-членів, скільки необхідно для конкретного екземпляра.

Повна схема бази даних формується в загальному випадку з множини різних типів набору і типів запису.

Ієрархічна деревоподібна структура, що орієнтована від коріння, задовольняє наступним умовам:

1) ієрархія завжди починається з кореневого вузла;

2) на першому рівні може знаходитися тільки один вузол- кореневий;

3) на нижніх рівнях знаходяться породжені (залежні) вузли;

4) кожний породжений вузол, який знаходиться на рівні і , зв'язаний тільки з одним вхідним вузлом , який знаходиться на рівні (і-1) ієрархії дерева;

5) кожний вхідний вузол може мати один або декілька породжених вузлів, які називаються подібними;

6) доступ до кожного породженого вузла виконується через йому відповідний вхідний вузол;

7) існує єдиний ієрархічний шлях доступу до будь-якого вузла, починаючи від кореневого вузла дерева.

Прикладами типових операторів маніпулювання ієрархічно- організованими даними можуть бути наступні:

· Знайти задане дерево БД ;

· Перейти від одного дерева до іншого;

· Перейти від одного запису до іншого в середині дерева ;

· Перейти від одного запису до іншого в порядку обходу ієрархії;

· Уставити новий запис у зазначену позицію;

· Видалити поточний запис.

Перевагами деревовидної моделі є наявність функціональних систем керування базами даних , які підтримують дану модель , простота сприйняття користувачами принципу ієрархії, забезпечення деякого рівня незалежності даних, простота оцінки операційних характеристик системи завдяки апріорно заданим взаємозв'язкам.

До недоліків ієрархічних структур відносять :

- надлишковість зберігання інформації, так як ієрархічні структури не підтримують взаємозв'язки Б:Б;

- строгу ієрархічну впорядоченість , яка ускладнює процедури включення та вилучення записів;

- вилучення вихідних вузлів призводить до вилучення відповідних їм породжених , що вимагає особливої обережності;

- ускладнюється доступ до даних , які лежать на більш низьких рівнях ієрархії, так як кореневий вузол завжди є головним, а доступ до любого породженого вузла може здійснюватись через вихідний.

Розглянемо в якості прикладу наступну задачу. Нехай необхідно побудувати ієрархічну базу даних про викладачів , студентів та дисципліни в наступних взаємозв'язках:

ВИКЛАДАЧ ДИСЦИПЛІНА

СТУДЕНТ ДИСЦИПЛІНА,

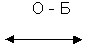де - відношення ОДИН - ДО -БАГАТЬОХ.

Ця інформація в ієрархічній моделі може бути представлена різними способами . Один з варіантів показаний на рис. 3.6 . Кореневим вузлом є об'єкт СТУДЕНТ. Для кожного студента при даному представленні є екземпляр кореневого вузла.

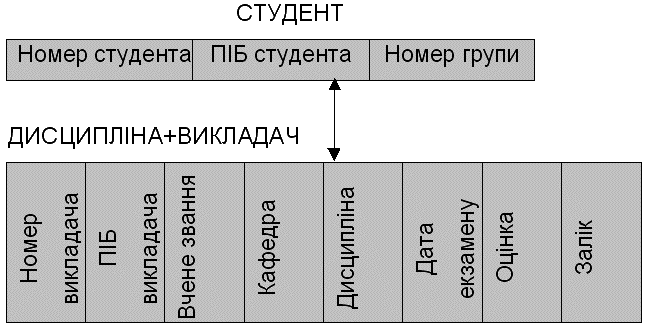
Рисунок 3.6 - Представлення бази даних (СТУДЕНТ-ДИСЦИПЛІНА) за допомогою ієрархічної моделі

Об'єкти ВИКЛАДАЧ, ДИСЦИПЛІНА об'єднані в породжуваний вузол ДИСЦИПЛІНА + ВИКЛАДАЧ. В кожний момент часу база даних, що задана моделлю рис. 3.6 , може мати записи для N студентів. На рис. 3.7 показаний екземпляр запису бази даних для студента Собко Н.Ю.

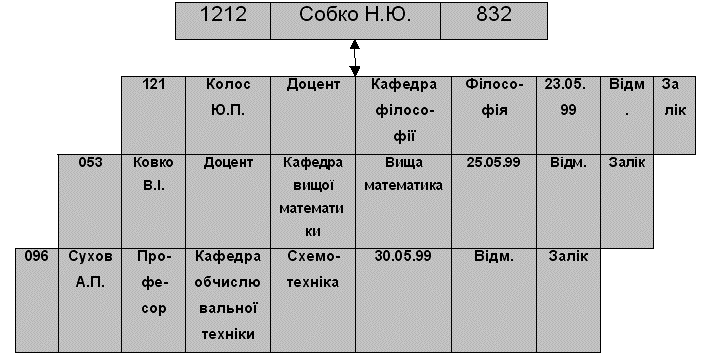
Рисунок 3.7 - Екземпляр запису ієрархічної бази даних СТУДЕНТ - ДИСЦИПЛІНА

Побудована модель дозволяє виконати такі операції , як оперативна видача інформації про здачу іспитів студентами по різним дисциплінам( отримати кількісну та якісну оцінки) . В той же час , якщо необхідно отримати інформацію про те, які викладачі по дисципліні "Схемотехніка " приймають іспити , то прийдеться переглянути всі записи породжуваних вузлів всіх екземплярів кореневого вузла . При такій постановці задачі більше підходить модель , яка представлена на рис.3.8 , де кореневим вузлом є об'єкт ВИКЛАДАЧ , а об'єкти СТУДЕНТ та ДИСЦИПЛІНА об'єднані в породжуваний вузол СТУДЕНТ+ ДИСЦИПЛІНА. Крім того , можна відмітити , що дані про викладачів та назви дисциплін в базі даних (див. рис. 3.6 ) повторюються в екземплярі породжуваного вузла стільки разів , скільки студентів навчаються у даного викладача.

В моделі на рис. 3.8 даними , що дублюються , є відомості про студентів.

Рисунок 3.8- Альтернативне представлення бази даних СТУДЕНТ-ДИСЦИПЛІНА

На прикладах (див. рис. 3.6 та 3.8 ) проілюструємо проблеми, які пов'язані з операціями включення та видалення даних.

З принципу ієрархії випливає, що екземпляр породжуваного вузла не може існувати у відсутності відповідного йому екземпляра вихідного вузла. Таким чином , неможливо без використання будь-яких інших методів включити в базу даних , представлену на рис. 3.6 , відомості про викладача, який не приймає іспити або заліки. Одним з методів реалізації такого включення є формування "пустих " екземплярів , які приводять до додаткових затрат зовнішньої пам'яті ЕОМ і до необхідності строгого обліку таких записів.

При видаленні екземплярів вихідного вузла автоматично видаляються всі екземпляри породжені вузлом. Наприклад, в базі даних, модель якої приведена на рис.3.8, при вилучені екземпляра ВИКЛАДАЧ потягне за собою і вилучення всіх екземплярів про студентів, які навчаються в даного викладача. Вказане повністю неприпустимо при розв'язку, наприклад, задачі оцінки якості навчання студентів.

В ієрархічні базі даних проблеми, пов'язані з операціями включення нових записів і вилучення старих, а також проблеми часткового дублювання інформації виникають в результаті того, що відношення БАГАТО-ДО-БАГАТЬОХ безпосередньо не підтримується, що і є основним недоліком ієрархічних моделей.

1. В чому полягають особливості структурної організації ієрархічних моделей даних ?

2. Чим обумовлено широке використання збалансованих дерев ?

3. Перечисліть типові оператори маніпулювання ієрархічними даними.

4. Перечисліть основні переваги та недоліки ієрархічних моделей даних .