Вінницький державний технічний університет містить море(!) аналітичної інформації

Основи реляційної алгебри

Реляційна модель баз даних надає можливість маніпулювати над доменами відношень. Для цих цілей існує два види апарата маніпулювання відношеннями: реляційна алгебра (алгебра відношень) і реляційне обчислення (обчислення відношень). маніпулювання відношеннями: реляційна алгебра (алгебра відношень) і реляційне обчислення (обчислення відношень).

Алгеброю відношень називають систему операцій маніпулювання відношеннями, кожний оператор якого в якості операнда (операндів) використовує одне чи більше відношень і утворює нове відношення по попередньо обумовленому правилу.

Реляційне обчислення дозволяє шляхом використання обчислення предикатів та кванторів змінних описувати відношення та операції над ними в вигляді аналітичного виразу або формули.

В реляційній алгебрі використовують п'ять основних операцій: об'єднання, різниця, декартовий добуток, проекція і селекція.

1.Проекція .Суть цієї операції полягає в тому, що береться відношення R, видаляються деякі з його компонентів і перевпорядковуються компоненти, що залишились. Якщо в результаті проекції появляються однакові кортежі, то вони з результуючого відношення вилучаються.

Операція проекції полягає в виділенні необхідних стовпців (доменів) з відношення .

Нехай дано відношення СТУДЕНТ-УСПІШНІСТЬ.

Таблиця 4.3 СТУДЕНТ-УСПІШНІСТЬ

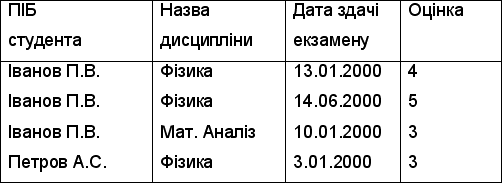
В результаті виконання операції проекції отримуємо нове відношення, яке представлено в табл. 4.4.

Таблиця 4.4 Приклад операції "проекція"

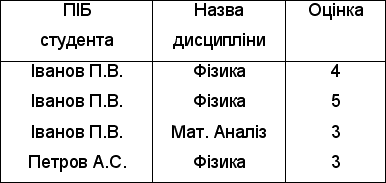
2. Об'єднання. Об'єднання відношень R і S (позначаться RИS) представляє собою множину кортежів, які належать R чи S або їм обом. Оператор об'єднання застосовується тільки до відношень однакової арності. Якщо в результаті об'єднання відношень мають місце однакові кортежі, то вони заміняються одним.

Нехай задано два відношення , представлені таблицями 4.5, 4.6 . Виконаємо над ними операцію об'єднання.

Таблиця 4.5 ВИКЛАДАЧІ-ДИСЦИПЛІНИ

Таблиця 4.6 ВИКЛАДАЧІ-ДИСЦИПЛІНИ

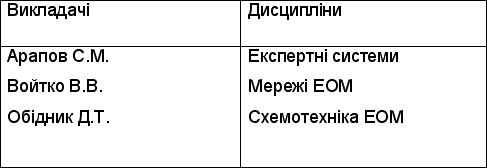
В результаті об'єднання відношень отримуємо результуюче відношення, яке представлено в табл.4.7.

Таблиця 4.7 ВИКЛАДАЧІ-ДИСЦИПЛІНИ

3.Різниця. Різницею відношення R і S( позначається як R-S), називається множина кортежів, які належать R, але не належать S (рис.4.5.). При реалізації різниці необхідно, щоб R і S мали одну і ту ж саму арність.

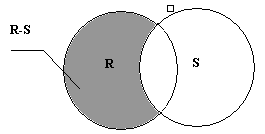
Рисунок 4. 5 -Графічна ілюстрація операції віднімання відношень

Якщо А - відношення про жителів мікрорайону, В- відношення про тих, хто пройшов медичний огляд, то відношення А-В буде містити дані про тих жителів мікрорайону, хто не пройшов медичний огляд.

4. Декартовий добуток. Нехай R і S - відношення арності k1 і k2 відповідно. Тоді декартовим добутком відношень R і S називається множина кортежів довжини k1 + k2, перші k1 компонентів яких утворюють кортежі, які належать R, а останні k2 - кортежі, що належать S. Наприклад :

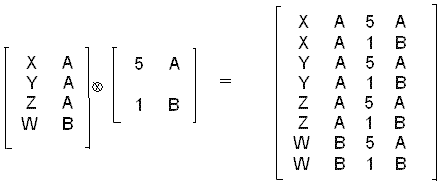
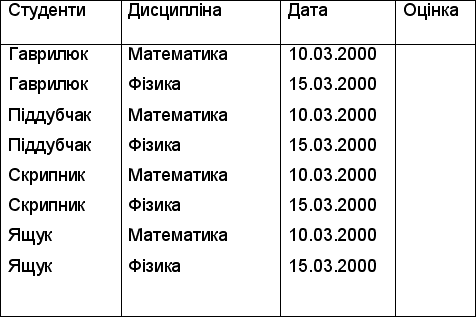
Результатом декартового добутку відношень СТУДЕНТИ (Табл. 4.8 ) та ЕКЗАМЕНИ (Табл. 4.9 ) буде відношення ЕКЗАМЕНАЦІЙНА ВІДОМІСТЬ (Табл. 4.10).

Таблиця 4.8---------------------- Таблиця 4.9 СТУДЕНТИ - ЕКЗАМЕНИ

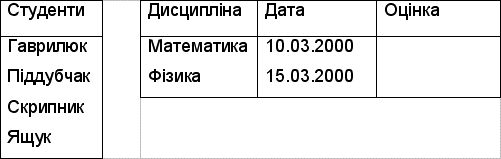
Таблиця 4.10 ЕКЗАМЕНАЦІЙНА ВІДОМІСТЬ

5. Селекція. Нехай F - формула, яка може бути утворена слідуючими засобами: а) операндами, які є константами чи номерами компонентів; б) арифметичними операторами порівняння <, =",">, №, і; в) логічними операторами Щ(І), Ъ(АБО), Ш(НІ).

В цьому випадку df (R) є множена кортежів t , які належать R, таких, що при підстановці i-го компонента t замість будь-якого входження номера i в формулу F для всіх i вона стане істиною.

Наприклад, d2>3 (R) означає множину кортежів, що належать R, другий компонент яких більше третього компонента.

Таблиця 4.11

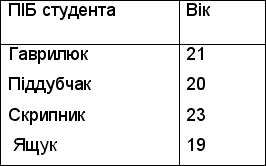
При реалізації селекції відношення, приведеного в табл.4.11 ,згідно ознаки ( вік>20) ,отримуємо відношення

Таблиця 4.12

Крім перерахованих операцій існують і інші, але всіх можна отримати з п'яти основних.

Розглянемо неосновні операції перетину та ділення.

Перетин R S двох відношень R та S знаходиться згідно формул R-(R-S).

Нехай R та S є відношення арності r і s відповідно, де r > s і S . Тоді частка R S є множина кортежів t довжини (r -s) таких, що для всіх кортежів u довжини s, які належать S, кортеж tu належить R.

Виконаємо операцію ділення над відношеннями, які представлені відповідно таблицями 4.13 та 4.14.

Таблиця 4.13 Екзаменаційна відомість

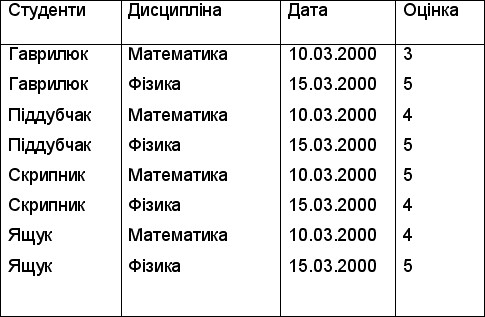
Таблиця 4.14

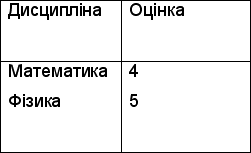
В результаті отримуємо частку

Таблиця 4.15

Схематично операції реляційної алгебри представлені на рис.4.6.

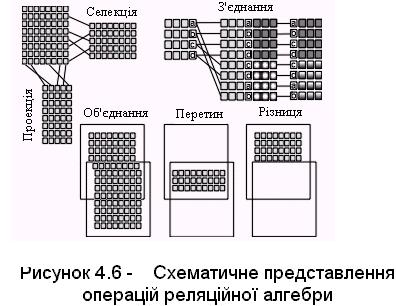
Розроблені мови маніпулювання даними, що дозволяють реалізувати всі операції реляційної алгебри і практично будь-які їхній сполучення. Серед них найбільше поширені SQL (Structured Query Language - структуризована мова запитів) і QBE (Quere-By-Example - запити за зразком) Обидві відносяться до мов дуже високого рівня, за допомогою яких користувач вказує, які дані необхідно одержати, не уточнюючи процедуру їхнього формування.

За допомогою єдиного запиту на любій із цих мов можна з'єднати декілька таблиць у тимчасову таблицю і вирізувати з неї необхідні рядки і стовпці (селекція і проекція).

Контрольні запитання.

1. Скільки основних операції використовується в реляційній алгебрі ?

2.Чи може відношення мати два однакових кортежі після виконання операцій проекції чи обєднання ?

3.Які основні операції використовуються при знаходженні частки ?

5. Як змінюється потужність відношень при виконанні операцій реляційної алгебри ?

Назад | Зміст | Вперед

Copyright ©VSTU
Created: November 16, 2000