Лабораторная работа

Вінницький державний технічний університет містить море(!) аналітичної інформації

Нормалізація схем баз даних

Нормалізація - це розбивка таблиці на дві або більш, які характеризуються кращими властивостями при доповненні , зміні і вилученні даних. Кінцева мета нормалізації зводиться до отримання такого проекту бази даних, у котрому кожний факт з'являється лише в однім місці, тобто виключена надлишковість інформації. Це робиться не стільки з метою економії пам'яті, скільки для виключення можливої суперечливості збережених даних.

Кожна таблиця в реляційній БД задовольняє умові, у відповідності з якою у позиції на перетині кожного рядка і стовпця таблиці завжди знаходиться єдине атомарне значення і ніколи не може бути множини таких значень. Будь-яка таблиця, що задовольняє цій умові, називається нормалізованою.

Кожній нормальній формі відповідає деякий визначений набір обмежень. Відношення знаходиться в деякій нормальній формі, якщо задовольняється властивий їй набір обмежень.

Кожна нормальна форма є більш обмеженою і більш бажаною, ніж попередня. Це зв'язано з тим, що в (N+1)-ій нормальній формі вилучаються деякі небажані властивості, які характерні N-ій нормальній формі. Теорія нормалізації грунтується на наявності тієї або іншої залежності між полями таблиці.

Основні властивості нормальних форм:

· кожна наступна нормальна форма в деякому змісті краще попередньої;

· при переході до наступної нормальної форми властивості попередніх нормальних властивостей зберігаються.

Найбільше важливі нормальні форми відношень грунтуються на фундаментальному в теорії реляційних баз даних понятті функціональної залежності.

Визначення 1. Функціональна залежність .

У відношенні R атрибут Y функціонально залежить від атрибута X (X і Y можуть бути складовими) у тому і тільки в тому випадку, якщо кожному значенню X відповідає в точності одне значення Y: X Y.

Визначення 2. Повна функціональна залежність.

Функціональна залежність X Y називається повною, якщо атрибут Y не залежить функціонально від будь-якої підмножини X.

Визначення 3. Транзитивна функціональна залежність .

Функціональна залежність називається транзитивною, якщо з функціональних залежностей X Y та Y Z випливає, що X Z.

Наприклад, Вінниця входить до Поділля, а Поділля -до України . Для даного прикладу має місце транзитивна залежність ВІННИЦЯ УКРАЇНА.

Визначення 4. Неключовий атрибут .

Неключовим атрибутом називається будь-який атрибут відношення, що не входить до складу первинного ключа .

Визначення 5. Взаємно незалежні атрибути .

Два або більш атрибути взаємно незалежні, якщо жодний із цих атрибутів не є функціонально залежним від інших.

Відношення R задано в першій нормальній формі, якщо воно задано у виді множини своїх кортежів , які не повторюються.

Для того, щоб представити відношення в першій нормальній формі необхідно над його кортежами виконати операцію проекції для видалення рядків, які повторюються.

Відношення R задано в другій нормальній формі, якщо воно, по-перше, є відношенням у першій нормальній формі і, по-друге, кожний його атрибут, який не є основним атрибутом, функціонально повно залежить від будь-якого можливого ключа цього відношення.

Нехай задано відношення ФАКУЛЬТЕТ ( НАЙМЕНУВАННЯ, ПІБ ДЕКАНА, ТЕЛЕФОН).

Відношення ФАКУЛЬТЕТ задано в другій нормальній формі, тому що у відношенні ФАКУЛЬТЕТ атрибут ТЕЛЕФОН, який не є основним, повністю залежить від будь-якого можливого ключа: НАЙМЕНУВАННЯ, ПІБ ДЕКАНА.

У загальному випадку, якщо всі можливі ключі відношення містять по одному атрибуту, то це відношення задане в другій нормальній формі, тому що в цьому випадку всі атрибути, які не є основними, функціонально повно залежать від можливих ключів. Однак це твердження не завжди справедливе, якщо ключ відношення R є складовим.

Розглянемо наступне відношення:

СТУДЕНТ-КУРС ПРОЕКТ (НОМЕР ЗАЛІКОВОЇ КНИЖКИ, КОД ПРЕДМЕТУ, ПРІЗВИЩЕ СТУДЕНТА, НОМЕР ГРУПИ, ВИКЛАДАЧ, ПРОЦЕНТ ВИКОНАННЯ).

Припустимо, що в одній групі можуть навчаються однофамільці. Тоді для цього відношення можливий тільки один ключ: НОМЕР ЗАЛІКОВОЇ КНИЖКИ, КОД ПРЕДМЕТУ. Виходячи з прийнятого припущення, атрибут ПРІЗВИЩЕ СТУДЕНТА не входить у ключ. Тоді атрибут НОМЕР ЗАЛІКОВОЇ КНИЖКИ не визначається значенням атрибута ПРІЗВИЩЕ СТУДЕНТА, тобто атрибути ПРІЗВИЩЕ СТУДЕНТА і НОМЕР ГРУПИ не є основними, але функціонально залежать від основного атрибута НОМЕР ЗАЛІКОВОЇ КНИЖКИ, що входить у складовий ключ. Функціональні залежності між атрибутами цього відношення показані на рис. 4.7.

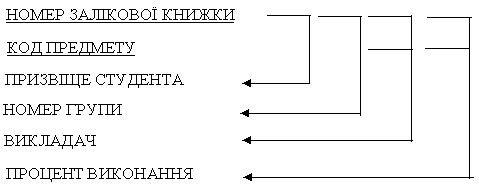
Рисунок 4.7 - Функціональна залежність

Розщепивши вихідне відношення на два нових у другій нормальній формі, можна усунути надлишковість (рис. 4.8 ). При виконанні цієї операції розбивки на два відношення враховано те, що атрибути, які функціонально залежать від одного основного атрибута разом із ним утворять одне відношення з єдиним ключем НОМЕР ЗАЛІКОВОЇ КНИЖКИ, а інші атрибути, які функціонально повно залежать від складового ключа ,залишено у вихідній схемі.

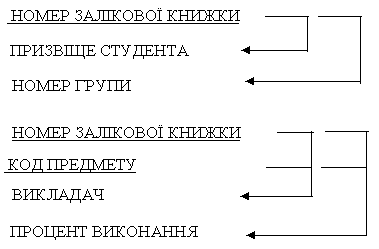
Рисунок 4.8 - Приклад усунення функціональної залежності

Розглянемо наступний приклад схеми відношення:

СПІВРОБІТНИКИ - ВІДДІЛИ - ПРОЕКТИ

(СПІВРОБ НОМЕР,СПІВРОБ ЗАРП, ВІДДІЛ НОМЕР, ПРО НОМЕР, СПІВРОБ ЗАВДАННЯ).

У відношенні використані скорочення : СПІВРОБ- співробітник, ЗАРП- зарплата, ПРО- проект.

Первинний ключ:

СПІВРОБ НОМЕР, ПРО НОМЕР.

Функціональні залежності:

СПІВРОБ НОМЕР -> СПІВРОБ ЗАРП

СПІВРОБ НОМЕР -> ВІДДІЛ НОМЕР

ВІДДІЛ НОМЕР -> СПІВРОБ ЗАРП

СПІВРОБ НОМЕР, ПРО НОМЕР -> СПІВРОБ ЗАВДАННЯ.

Хоча первинним ключем є складовий атрибут СПІВРОБ НОМЕР, ПРО НОМЕР, атрибути СПІВРОБ ЗАРП і ВІДДІЛ НОМЕР функціонально залежать від частини первинного ключа, тобто атрибута СПІВРОБ НОМЕР. В результаті, неможливо вставити у відношення СПІВРОБІТНИКИ - ВІДДІЛИ - ПРОЕКТИ кортеж, що описує співробітника, який ще не виконує ніякого проекту (первинний ключ не може містити невизначене значення). При видаленні кортежу не тільки руйнується зв'язок даного співробітника з даним проектом, але втрачається інформацію про те, що він працює в деякому відділі. При переводі співробітника в інший відділ необхідно модифікувати всі кортежі, які описують цього співробітника, або одержимо неузгоджений результат. Такі неприємні явища називаються аномаліями схеми відношення. Вони усуваються шляхом нормалізації.

Виконаємо декомпозицію відношення СПІВРОБІТНИКИ - ВІДДІЛИ в два відношення СПІВРОБІТНИКИ - ВІДДІЛИ і СПІВРОБІТНИКИ - ПРОЕКТИ :

СПІВРОБІТНИКИ - ВІДДІЛИ

(СПІВРОБ НОМЕР, СПІВРОБ ЗАРП, ВІДДІЛ НОМЕР)

Первинний ключ:

СПІВРОБ НОМЕР

Функціональні залежності:

СПІВРОБ НОМЕР -> СПІВРОБ ЗАРП

СПІВРОБ НОМЕР -> ВІДДІЛ НОМЕР

ВІДДІЛ НОМЕР -> СПІВРОБ ЗАРП

СПІВРОБІТНИКИ - ПРОЕКТИ

(СПІВРОБ_НОМЕР, ПРО НОМЕР, СПІВРОБ ЗАВДАННЯ)

Первинний ключ:

СПІВРОБ НОМЕР, ПРО НОМЕР

Функціональна залежність:

СПІВРОБ НОМЕР, ПРО НОМЕР -> СПІВРОБ_ЗАВДАННЯ

Кожне з цих двох відношень знаходиться в 2НФ і в них усунуті відзначені вище аномалії .

Відношення R знаходиться в третій нормальній формі (3НФ) у тому і тільки в тому випадку, якщо знаходиться в 2НФ і кожний неключовий атрибут нетранзитивно залежить від первинного ключа.

Наприклад, відношення:

ГУРТОЖИТОК (ПІБ СТУДЕНТА, НОМЕР ГРУПИ, НОМЕР КІМНАТИ, СТАРОСТА КІМНАТИ) знаходиться в другій нормальній формі, але не в третій, тому що атрибут СТАРОСТА КІМНАТИ залежить від атрибута НОМЕР КІМНАТИ, який у свою чергу залежить від атрибута ПІБ СТУДЕНТА і, отже, СТАРОСТА КІМНАТИ транзитивно залежить від ПІБ СТУДЕНТА. Це відношення можна привести до необхідної форми шляхом його розщеплення на два:

СТУДЕНТ-ГУРТОЖИТОК (ПІБ СТУДЕНТА, НОМЕР ГРУПИ, НОМЕР КІМНАТИ),

КІМНАТА -ГУРТОЖИТОК (НОМЕР КІМНАТИ. СТАРОСТА КІМНАТИ).

Залежності між атрибутами вихідного й отриманих відношень подані на рис. 4.9 , звідки видно, що отримані відношення більш доцільніші від вихідного. Так, інформація про старосту кімнати може знадобитися незалежно від інформації про студентів, що проживають у цій кімнаті.

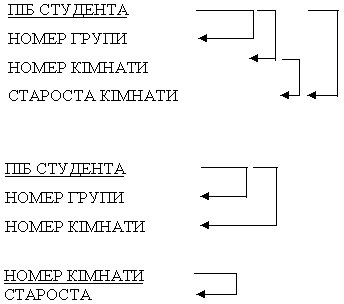
Рисунок 4.9 - Приклад усунення транзитивної залежності

Нехай маємо відношення (ФІРМА, СКЛАД, ОБ'ЄМ ).

Для даного відношення характерні наступні аномалії.

1. Якщо в даний момент відсутня фірма, яка отримує товар зі складу, то в базу даних неможливо ввести інформацію про об'єм складу.

2. Якщо фірма перестає отримувати товар зі складу, то данні про склад та його об'єм не можна зберігати в базі даних.

3. Якщо об'єм складу змінився, то необхідно переглянути всі рядки відношення і змінити кортежі для форм, пов'язаних зі складом.

Причиною аномалій для даного відношення є наявність транзитивного зв'язку між атрибутами.

Для усунення аномалій розіб'ємо вихідне відношення на два :

ЗБЕРІГАННЯ ( ФІРМА, СКЛАД),

ОБ'ЄМ (СКЛАД, ОБ'ЄМ).

На практиці в більшості випадків три нормальні форми схем відношень є достатніми і приведенням до третьої нормальної форми процес проектування реляційної бази даних , як правило, закінчується. Однак іноді корисно продовжити процес нормалізації.

Розглянемо наступний приклад схеми відношення:

СПІВРОБІТНИКИ-ПРОЕКТИ (СПІВРОБІТНИКА НОМЕР, СПІВРОБІТНИКА ПРИЗВІЩЕ, ПРОЕКТУ НОМЕР, СПІВРОБІТНИКА ЗАВДАННЯ) .

Можливі ключі (звернете увагу, що на цій стадії нормалізації в увагу приймаються існування можливих ключів):

СПІВРОБІТНИКА НОМЕР, ПРОЕКТУ НОМЕР

СПІВРОБІТНИКА ПРИЗВІЩЕ, ПРОЕКТУ НОМЕР .

Функціональні залежності:

СПІВРОБІТНИКА НОМЕР -> СПІВРОБІТНИКА ПРИЗВІЩЕ

СПІВРОБІТНИКА НОМЕР -> ПРОЕКТУ НОМЕР

СПІВРОБІТНИКА ПРИЗВІЩЕ -> СПІВРОБІТНИКА НОМЕР

СПІВРОБІТНИКА ПРИЗВІЩЕ -> ПРОЕКТУ НОМЕР

СПІВРОБІТНИКА НОМЕР, ПРОЕКТУ НОМЕР -> СПІВРОБІТНИКА

ЗАВДАННЯ

СПІВРОБІТНИКА ПРИЗВІЩЕ, ПРОЕКТУ НОМЕР ->

СПІВРОБІТНИКА ЗАВДАННЯ

У цьому прикладі припускаємо, що особистість співробітника цілком визначається як його номером, так і прізвищем.

Незалежно від того, який із можливих ключів обраний у якості первинного ключа, ця схема знаходиться в 3НФ. Однак той факт, що є функціональні залежності атрибутів відношення від атрибута, що є частиною первинного ключа, приводить до аномалій. Наприклад, для того, щоб змінити ПРИЗВІЩЕ співробітника з даним номером погодженим способом, буде потрібно модифікувати всі кортежі, які включають його номер. Введемо визначення.

Детермінантом називається будь-який атрибут, від котрого функціонально повно залежить деякий інший атрибут.

Нормальна форма Бойса-Кодда. Відношення R знаходиться в нормальній формі Бойса-Кодда (БКНФ) у тому і тільки в тому випадку, якщо кожний детермінант є можливим ключем.

Зауважимо, що якщо у відношенні є тільки один можливий ключ (який є первинним ключем), те це визначення стає еквівалентним визначенню третьої нормальної форми.

Очевидно, що ця вимога не виконана для відношення СПІВРОБІТНИКИ-ПРОЕКТИ. Можна зробити його декомпозицію до відношень СПІВРОБІТНИКИ і СПІВРОБІТНИКИ-ПРОЕКТИ:

СПІВРОБІТНИКИ (СПІВРОБІТНИКА НОМЕР, СПІВРОБІТНИКА ПРИЗВІЩЕ) .

Можливі ключі:

СПІВРОБІТНИКА НОМЕР

СПІВРОБІТНИКА ПРИЗВІЩЕ

Функціональні залежності:

СПІВРОБІТНИКА НОМЕР -> СПІВРОБІТНИКА ПРИЗВІЩЕ

СПІВРОБІТНИКА ПРИЗВІЩЕ -> СПІВРОБІТНИКА НОМЕР

СПІВРОБІТНИКИ-ПРОЕКТЫ (СПІВРОБІТНИКА НОМЕР,

ПРОЕКТУ НОМЕР, СПІВРОБІТНИКА ЗАВДАННЯ)

Можливий ключ:

СПІВРОБІТНИКА НОМЕР, ПРОЕКТУ НОМЕР

Функціональні залежності:

СПІВРОБІТНИКА НОМЕР, ПРОЕКТУ НОМЕР -> СПІВРОБІТНИКА ЗАВДАННЯ.

Можлива альтернативна декомпозиція, якщо вибрати за основу СПІВРОБІТНИКА ПРИЗВІЩЕ. У обох випадках отримані відношення СПІВРОБІТНИКИ і СПІВРОБІТНИКИ-ПРОЕКТИ знаходяться в БКНФ, і їм не властиві відзначені аномалії.

Розглянемо відношення

R (МІСТО, АДРЕСА, ІНДЕКС).

Атрибут ІНДЕКС визначає індекс відділення зв'язку, яке обслуговує адресатів деякої вулиці міста, АДРЕСА - назву вулиці і номеру будинку. При цьому будемо припускати, що кортеж (С, S, Z) належить деякому відношенню зі схемою відношення R, якщо тільки в місті С є будинок за адресою S і Z є відповідним поштовим індексом. У цьому випадку мають місце наступні функціональні залежності:

МІСТО, АДРЕСА ІНДЕКС,

ІНДЕКС МІСТО.

Іншими словами, повна адреса (назва міста і адреса в місті) визначає поштовий індекс, а поштовий індекс, у свою чергу, визначає назву міста, але не визначає адресу, тому що одне відділення зв'язку обслуговує багато будинків на різних вулицях. Таким чином, в якості основного ключа можна вибрати одне з двох множин атрибутів:

МІСТО, АДРЕСА і

АДРЕСА, ІНДЕКС .

Схема відношення R (МІСТО, АДРЕСА, ІНДЕКС) не знаходиться в нормальній формі Бойса-Кода, так як має місце залежність ІНДЕКС МІСТО. Декомпозицією відношення його можна привести до нормальної форми Бойса-Кода.

Розглянемо приклад наступної схеми відношення:

ПРОЕКТИ( ПРОЕКТУ НОМЕР, ПРОЕКТУ СПІВРОБ, ПРОЕКТУ ЗАВДАННЯ) .

Відношення ПРОЕКТИ містить номера проектів, кожний проекту - список співробітників, які можуть виконувати проект, і список завдань, які передбачаються проектом. Співробітники можуть брати участь у декількох проектах, і різні проекти можуть включати однакові завдання.

Кожний кортеж відношення зв'язує деякий проект із співробітником, які беруть у цьому проекті, і з завданням, котре співробітник виконує в рамках даного проекту (припускаємо, що будь-який співробітник, який бере участь у проекті, виконує всі завдання, передбачені цим проектом). Через сформульовані вище умови єдиним можливим ключем відношення є складовий атрибут ПРОЕКТ НОМЕР, ПРОЕКТ СПІВРОБ, ПРОЕКТ ЗАВДАННЯ, і немає ніяких інших детермінантів. Отже, відношення ПРОЕКТИ знаходиться в БКНФ. Але при цьому воно має аномалії: якщо, наприклад, деякий співробітник приєднується до даного проекту, необхідно вставити у відношення ПРОЕКТИ стільки кортежів, скільки завдань у ньому передбачено.

У відношенні R (A, B, C) існує багатозначна залежність (multi-valued dependence - MVD) R. A R. B в тому і тільки в тому випадку, якщо множина значень B, що відповідає парі значень A і C, залежить тільки від A і не залежить від С.

У відношенні ПРОЕКТИ існують наступні дві багатозначні залежності:

ПРОЕКТ НОМЕР ПРОЕКТ СПІВРОБ

ПРОЕКТ НОМЕР ПРОЕКТУ ЗАВДАННЯ .

Неважко показати, що в загальному випадку у відношенні R (A, B, C) існує багатозначна залежність A B у тому і тільки в тому випадку, коли існує багатозначна залежність A C.

Відношення R знаходиться в четвертій нормальній формі (4НФ) у тому і тільки в тому випадку, якщо у випадку існування багатозначної залежності A B всі інші атрибути R функціонально залежать від A.

У нашому прикладі можна виконати декомпозицію відношення ПРОЕКТИ на два відношення

ПРОЕКТИ-СПІВРОБІТ і ПРОЕКТИ-ЗАВДАННЯ:

ПРОЕКТИ-СПІВРОБІТ ( ПРОЕКТ НОМЕР, ПРОЕКТ СПІВРОБІТ)

ПРОЕКТИ-ЗАВДАННЯ ( ПРОЕКТ НОМЕР, ПРОЕКТ ЗАВДАННЯ).

Обидва ці відношення знаходяться в 4НФ .

Розглянемо ще один приклад.

Нехай задано відношення

R (СТУДЕНТ, ТОВАРИСТВО, СУСПІЛЬНА РОБОТА, РІК).

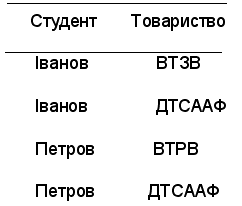
Атрибут ТОВАРИСТВО визначає назву товариств, членом яких є студент; атрибути СУСПІЛЬНА РОБОТА І РІК - найменування суспільних доручень, виконуваних студентом, і рік їх призначення. Передбачається, що те саме суспільне навантаження не може бути призначена двічі протягом одного року тому самому студенту, але заміна одного навантаження на інше протягом року допускаються. У табл. 4.16 приведений фрагмент відношення .

Таблиця 4.16. Приклад відношення з нетривіальними залежностями

Виділимо нетривіальні багатозначні залежності:

СТУДЕНТ ТОВАРИСТВО,

СТУДЕНТ (СУСПІЛЬНА_РОБОТА, РІК) .

Вважаємо, що атрибут ТОВАРИСТВО не залежить від того, яку суспільну роботу веде студент. Атрибути СУСПІЛЬНА РОБОТА і РІК взаємозалежні.

Наявність подібних нетривіальних багатозначних залежностей у схемі одного відношення і незалежність їхніх правих частин в остаточному підсумку приводять до комбінації значень правих частин, що ілюструється в табл. 4.16. Відомості про те, що студент Іванов є старостою групи у 1999 р. повторюються двічі в силу того, що він є членом двох товариств (ВТВР, ДТСААФ). Для студента Петрова в зв'язку зі зміною суспільної роботи (1999 - 2000 р.) доводиться вводити додаткові кортежі, у яких буде повторюватися інформація про членство студента в товариствах ВТВР і ДТСААФ.

Незважаючи на виникаючу при цьому надлишковість відношення R, воно подано в третій нормальній формі, тому що в цьому відношенні відсутні функціональні залежності. З метою усунення надлишковості у відношенні, поданій в третій нормальній формі, необхідно виконати розкладання по багатозначній залежності даного відношення( див табл. 4.17, 4.18 ).

Таблиця 4.17 Приклад відношення в четвертій нормальній формі

Таблиця 4.18.

Приклад відношення четвертій нормальній формі

В усіх розглянутих до цього часу нормалізаціях здійснювалась декомпозиція одного відношення на два. Іноді це зробити не вдається, але можлива декомпозиція в більше число відношень, кожне з який має кращі властивості.

Розглянемо, наприклад, відношення

СПІВРОБІТНИКИ-ВІДДІЛИ-ПРОЕКТИ(СПІВРОБ НОМЕР,

ВІДДІЛУ НОМЕР, ПРОЕКТУ НОМЕР) .

Припустимо, що той самий співробітник може працювати в декількох відділах і в кожному відділі брати участь у декількох проектах. Первинним ключем цього відношення є повна сукупність його атрибутів. Відсутні функціональні і багатозначні залежності.

Тому відношення знаходиться в 4НФ. Однак у ньому можуть існувати аномалії, які можна усунути шляхом декомпозиції на три відношення.

Відношення R (X, Y, ... , Z) задовольняє залежності з'єднання * (X, Y, ... , Z) у тому і тільки в тому випадку, коли R відновлюється без втрат шляхом з'єднання своїх проекцій на X, Y, ... , Z.

Відношення R знаходиться в п'ятій нормальній формі у тому і тільки в тому випадку, коли будь-яка залежність з'єднання в R випливає з існування деякого можливого ключа в R.

Введемо наступні імена складових атрибутів:

З = {СПІВРОБ_НОМЕР, ВІДДІЛУ_НОМЕР}

СП = { СПІВРОБ _НОМЕР, ПРОЕКТУ_НОМЕР}

ВП = {ВІДДІЛУ_НОМЕР, ПРОЕКТУ_НОМЕР}.

Припустимо, що у відношенні СПІВРОБІТНИКИ-ВІДДІЛИ-ПРОЕКТИ існує залежність з'єднання: * (З, СП, ОП)

На прикладах можна легко показати, що при вставках і видаленнях кортежів можуть виникнути проблема. Їх можна усунути шляхом декомпозиції вихідного відношення на три нових відношення:

СПІВРОБІТНИКИ-ВІДДІЛИ (СПІВРОБ_НОМЕР, ВІДДІЛУ_НОМЕР)

СОТРУДНИКИ-ПРОЕКТИ (СПІВРОБ_ НОМЕР, ПРОЕКТУ_НОМЕР)

ВІДДІЛИ-ПРОЕКТИ (ВІДДІЛУ НОМЕР, ПРОЕКТУ НОМЕР).

П'ята нормальна форма - це остання нормальна форма, яку можна одержати шляхом декомпозиції

На закінчення приведемо послідовність етапів нормалізації:

1. Перехід від структурної моделі даних до плоских двовимірних відношень (таблицям).

2. Усунення всіх неповних залежностей атрибутів, які не є основними, від усіх ймовірних ключів.

3. Усунення всіх транзитивних залежностей атрибутів, які не є основними, від усіх ймовірних ключів.

4. Усунення всіх нетривіальних багатозначних залежностей атрибутів, які не є основними, від усіх ймовірних ключів.

Після того як визначені елементи даних і залежності між ними, ці етапи в принципі можуть бути виконані автоматично по приведеному алгоритмі.

Контрольні запитання.

1. Для чого виконується нормалізація відношень ?

2. Які залежності між атрибутами називають транзитивними та функціонально повними ?

3. Приведіть приклади відношень в різних нормальних формах.

4. Приведіть послідовність етапів нормалізації.

Назад | Зміст | Вперед