1.8. Формули Бернуллі і Пуассона. Повторення дослідів

Нехай проводиться n незалежних випробувань, в результаті кожного з яких може відбутись або не відбутись деяка подія А. Нехай в кожному випробуванні ймовірність появи А рівна Р(А)=p і ймовірність протилежної події рівна . Визначимо ймовірність того, що подія А відбудеться m раз в n випробуваннях. При цьому побачимо, що появи або непояви події А можуть чергуватись довільним способом. Умовимося записувати можливі результати випробувань у вигляді комбінації букв А і . Наприклад, запис означає, що в чотирьох випробуваннях подія А відбулась в 1-му і 4-му випадках і не відбулась в 2-му і 3-му випадках.

Кожну комбінацію, в яку А входить m раз і входить n-m раз, назвемо сприятливою. Кількість сприятливих комбінацій дорівнює кількості k способів, якими можна вибирати m елементів із даних n; таким чином вона рівна числу сполучень із n елементів по m; тобто .

Обчислимо ймовірності сприятливих комбінацій. Розглянемо спочатку випадок коли подія А відбувається в перших m іспитах і значить не відбувається в інших n-m іспитах. Така сприятлива комбінація має вигляд: . Ймовірність цієї комбінації на основі теореми множення ймовірностей для незалежних подій дорівнює:

.

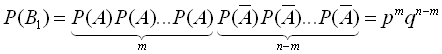В іншій сприятливій комбінації подія А зустрічається m раз, а подія відбувається n-m раз, тільки в іншому порядку, ймовірність кожної з таких комбінацій також рівна .

.

Всі сприятливі комбінації є несумісними. На основі теореми додавання несумісних подій:

;

або

.

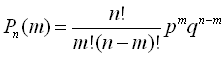Одержана формула є формулою Бернуллі.

Формула Бернуллі при різних m утворює суму:

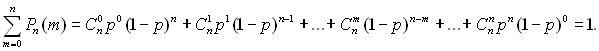Члени суми збігаються з членами розкладу бінома Ньютона.

.

Сума всіх можливих ймовірностей дорівнює 1, тому що , а . Сукупність імовірностей називається ще біноміальним розкладом ймовірностей.

Зауваження. При дослідженні багатьох питань потрібно обчислити ймовірність того, що подія А відбудеться “хоча б один раз”. Ця ймовірність визначиться з рівності: .

Імовірність того, що подія відбудеться не менше, ніж k раз, визначиться за формулою: 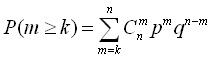або

.

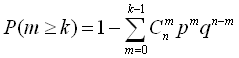Відмічене співвідношення (ratio) дає можливість ввести для обчислення ймовірності можливого числа події А в серії із n незалежних випробувань так звану твірну функцію (produced function):

.

Ця функція має таку властивість: коефіцієнт при x^m в записаному розкладі дорівнює ймовірності події А з’явитись рівно m раз в серії з n незалежних випробувань, які проводяться в змінних умовах. Так, наприклад, якщо ймовірність появи події в і-му випробуванні , а ймовірність непояви , то ймовірність появи А в n випробуваннях рівно m раз дорівнює коефіцієнту при в розкладі за степенями х твірної функції:

.

Приклад. Чотири лучники незалежно один від одного роблять по одному пострілу в мішень. Ймовірність попадання в мішень для першого стрілка рівна 0,8; для другого – 0,7; для третього – 0,6; для четвертого – 0,5. Знайти ймовірність того, що в мішені буде рівно дві пробоїни.

Розв’язання.

Ймовірності попадання для стрілків різні, тобто для розв’язування задачі використаємо твірну функцію. Згідно з умовою, твірна функція для даного прикладу має вигляд:

.

Коефіцієнт при є шуканою ймовірністю, тобто .

Іменем Пуассона часто називають випадкові процеси (random processes), що відбуваються в різних сферах технічних наук та досліджуються вченими.

Теорія броунівського руху (Brownian motion), що виходить з теоретико-імовірнісних передумов, була розроблена в 1905 р. двома відомими фізиками М. Смолуховським (1872-1917) та А. Ейнтейном (1879-1955). Пізніше висловлені ними ідеї використовувалися неодноразово як при вивченні фізичних явищ, так і в різних інженерних задачах. Зокрема, саме з цих робіт, як, втім, і з робіт Ерланга, проявився широкий інтерес до процесу Пуассона. Втім, сам Пуассон ввів у розгляд тільки розподіл Пуассона, але він заслужив, щоб його ім'я згадувалося і при розгляді випадкових процесів, пов'язаних з його розподілом. Це не єдиний випадок, коли на честь того чи іншого дослідника новим поняттям присвоюються їх імена, хоча до цих понять вони і не причетні. Тепер широко поширені гауссівські випадкові процеси, хоча сам Гаусс про них не мав жодного уявлення, та й сам розподіл задовго до його народження було отримано Муавром, Лапласом та ін.