3.4. Геометричний закон розподілу

Нехай здійснюються незалежні випробування, в кожному з яких імовірність появи події дорівнює p, непояви (1-p=q).

Випробування припиняються з появою події А. Нехай у перших k-1 випробуваннях подія А не відбулася, а в k-му випробуванні відбулась. Імовірність цієї події дорівнює Р(. Такий розподіл називають геометричним.

Математичне сподівання геометричного розподілу:

.

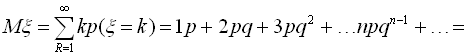
Дослідимо на збіжність ряд, що міститься у квадратних дужках. Для цього знайдемо його n-ну частинну суму:

S_n=1+2q+3q.

Помножимо обидві частини цієї рівності на q:

S_nq=q+2q.

Віднімемо від першої рівності другу:

S_n-S_nq=1+q+q.

Перші n членів є геометричною прогресією зі знаменником q і першим членом одиницею. Тому 1+q+q.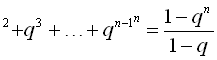

Тоді                          S_n(1-q)=.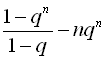

Звідси S_n=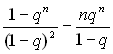. Враховуючи, що 0, знаходимо

.

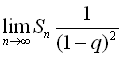Отже, М.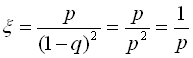

Дисперсію знаходимо за формулою: D.

(M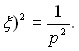

Знайдемо

Можна показати, що.

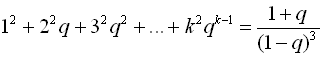Тоді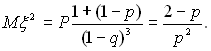                    

Отже, D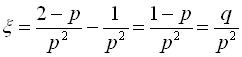; .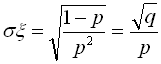