6.3. Властивості точкових оцінок

Розглянемо таку задачу. Є випадкова величина ξ, її закон розподілу містить невідомий теоретичний параметр а. Потрібно на основі дослідних даних знайти оцінку параметра а. Позначимо через х₁, х₂,..., х_n значення випадкової величини ξ, які одержують в результаті проведених n незалежних дослідів.

Нехай величина , обчислена на основі дослідних даних, є оцінкою параметра а. Це означає, що є функцією величин х₁, х₂, ..., х_n, крім того, значення х₁, х₂, ..., х_n слід розглядати як випадкові величини, кожна з яких розподілена за тим самим закону, що ξ. Тому є також випадковою величиною, закон розподілу якої залежить, по-перше, від закону розподілу випадкової величини ξ, по-друге, від числа дослідів n. Для того, щоб оцінка мала практичну цінність, вона повинна мати такі властивості:

1. Незміщеність оцінки.

Розрізняють оцінки зміщені і незміщені. Зміщеними називаються оцінки, математичне сподівання яких не дорівнює оцінювальному параметру:

.

Незміщеними називаються оцінки, для яких виконується умова:

.

Природно, за наближений параметр брати незміщені оцінки для того, щоб не робити систематичної помилки в сторону підвищення або зниження цієї оцінки.

2. Обгрунтовані або слушні оцінки.

Оцінка для параметра називається обгрунтованою, якщо вона збігається за імовірністю до оцінювального параметра при необмеженому зростанні числа досліджень n, тобто:

(6.1)

де ε – як завгодно мале додатне число. Для задоволення цієї вимоги досить, щоб дисперсія оцінки прямувала до нуля при n→∞, тобто, щоб виконувалась умова:

(6.2)

і щоб оцінка була незміщеною. Від (6.1) легко перейти до (6.2), якщо скористатись нерівністю Чебишова. Отже, обгрунтованість оцінки означає, що при достатньо великій кількості випробувань n з як завгодно великою вірогідністю відхилення оцінки від істинного значення параметра менше будь-якої наперед заданої величини.

Очевидно, такі вимоги повинна задовольняти кожна оцінка, придатна для практичного використання.

3. Ефективність оцінки.

Оцінки, які мають властивості незміщеності і обґрунтованості, при обмеженому числі дослідів можуть відрізнятися дисперсіями.

Очевидно, що чим менша дисперсія оцінки, тим менша ймовірність грубої помилки при визначенні наближеного значення параметра. Тому необхідно, щоб дисперсія оцінки була мінімальною, тобто щоб виконувалась умова:

.

Оцінка, що має таку властивість, називається ефективною (effective).

З метою отримання оцінок, які приймають як приблизні значення вихідних параметрів, необхідно користуватись сформульованими властивостями оцінок.

6.4. Визначення приблизного значення вимірюваної величини і приблизного значення дисперсії в випадку прямих рівномірних вимірювань

Визначити приблизне значення вимірюваної величини ξ – це означає провести оцінку математичного сподівання величини ξ. При цьому, якщо вимірювана величина ξ постійна, то оцінка для Мξ  приблизне значення справжнього значення вимірюваної величини, а якщо вимірювана величина випадкова, то оцінка для Мξ є приблизне значення математично сподівання вимірюваної випадкової величини ξ.

Необхідність отримання за дослідженими даними приблизного значення дисперсії виникає в зв’язку із визначенням характеристики точності або характеристики розсіювання випадкової величини.

Нехай є випадкова величина ξ з математичним сподіванням Мξ і дисперсією Dξ (або параметри невідомі). Потрібно на основі дослідних даних знайти обґрунтовані і незміщені оцінки цих параметрів. Позначимо через х₁, х₂, ..., х_n значення випадкової величини ξ, що спостерігалися в результаті проведення n незалежних рівноточкових вимірювань, тобто вимірювань, проведених в однакових умовах. Вважають ці умови виконаними, якщо вимірювання проводиться одним приладом. Природно, за оцінки математичного сподівання прийняти середнє арифметичне спостережуваних значень, які ми обчислили через: 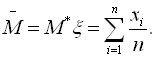Покажемо, що ця оцінка є обґрунтованою і незмінною. Дійсно, згідно з законом великих чисел:

.

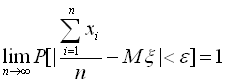Це означає, що є обґрунтованою оцінкою. Оцінка є також незміщеною або

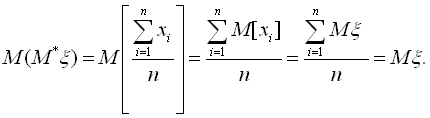(6.3)

Це слідує з того, що значення х₁, х₂, ..., х_n розглядаються як випадкові величини, кожна із яких розподілена за тим же законом, що і випадкова величина ξ. Перейдемо до оцінки дисперсії Dξ. Візьмемо статистичну дисперсію і перевіримо її на обґрунтованість і незміщеність. Статистична дисперсія має вигляд:

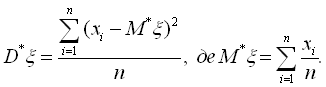(6.4)

Перетворимо вираз до вигляду:

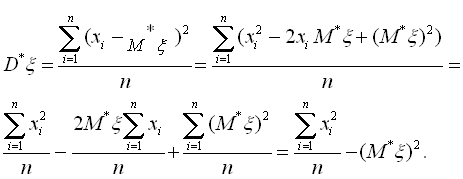(6.5)

Перший член у правій частині останнього рівняння являє собою середнє арифметичне n спостережених значень випадкової величини ξ² 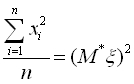; він збігається за імовірністю до М(ξ²). Другий член збігається за імовірністю до . Це означає, що вся права частина рівності збігається за імовірністю до величини .

Отже, статистична дисперсія D^*ξ є обгрунтованою оцінкою дисперсії Dξ. Перевіримо, чи є оцінка також незміщеною. Для цього в формулу (6.5) замість підставимо вираз із формули (6.4) і проведемо вказані дії:

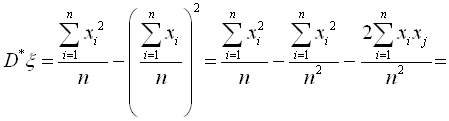
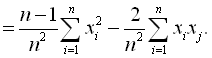          (6.6)

Оскільки дисперсія Dξ не залежить від того, в якій точці виберемо початок координат, то виберемо початок в точці Мξ і знайдемо математичне сподівання величини (6.6):

.

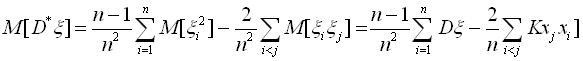З незалежності випробувань випливає, що Кх_i,х_j = 0, отже, рівність приймає вигляд: 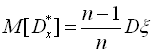. Звідси видно, що статистична дисперсія Dξ^* не є незміщеною оцінкою для дисперсії Dξ, її математичне сподівання не дорівнює Dξ, а трохи менше. Якщо помножити величину Dξ^* на , то ми отримаємо оцінку для дисперсії Dξ яка є незміщеною, тому що 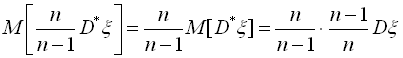. Оскільки множник прямує до одиниці при n→∞, то оцінка 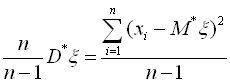буде також і обгрунтованою.

Таким чином, якщо в результаті проведених n незалежних вимірювань випадкової величини ξ з невідомим математичним оцінюванням Мξ і дисперсією Dξ отримаємо значення: х₁, х₂,...,х_n, то для визначення цих параметрів слід користуватися такими приблизними оцінками:

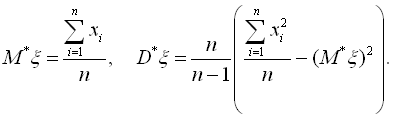(6.7)

Зазначимо, що за оцінку для дисперсії випадкової величини ξ з відомим математичним сподіванням Мξ необхідно брати статистичну дисперсію 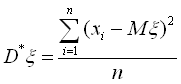. В цьому випадку статистична дисперсія задовольняє умови незміщеності і обґрунтованості.