6.6. Правила правдивості гіпотез

Постановка задачі. Нехай на основі даного статистичного матеріалу нам потрібно перевірити гіпотезу Н; яка твердить, що випадкова величина має функцію розподілу F(x).

Для того, щоб прийняти або спростувати гіпотезу Н, будемо розглядати випадкову величину η(y), що характеризує ступінь розходження теоретичних і статистичних тверджень. Величину η можна вибрати різними способами. Наприклад, за η(y) можна взяти максимальне відхилення статистичної функції розподілу від теоретичної F(x)

Закон розподілу випадкової величини η(y_і) залежить від закону розподілу випадкової величини ξ, над якою виконувались досліди, і від числа дослідів n.

Нехай в результаті проведених n дослідів над випадковою величиною ξ величина η прийняла значення у. Запитується, чи можна пояснити прийняте значення η випадковими причинами, або ж це значення занадто велике і вказує на наявність суттєвої різниці між теоретичним і статистичним розподілом, тобто на хибність гіпотези Н?

Нехай гіпотеза Н істинна. Знайдемо імовірність того, що випадкова величина η за рахунок випадкових причин, по’язаних з обмеженим числом дослідного матеріалу, прийме значення не менше, чим дослідне значення у, тобто знайдемо ймовірність . Якщо ця ймовірність мала, то гіпотезу Н слід спростувати як малоімовірну, якщо ця імовірність велика, то експериментальні дані не протирічать гіпотезі Н.

Найбільш простим методом перевірки гіпотез є так званий критерій згоди академіка А. М. Колмогорова.

Схема застосування А. М. Колмогорова:

1. За результатами n проведених вимірювань будується статистична функція розподілу F^*(x);

2. На тому ж графікові будується запропонована теоретична функція розподілу F(x);

3. Визначається максимальна величина модуля відмінності їх ординат

Колмогоров А. М. довів, що який би вигляд не мала неперервна функція розподілу F(x) при необмеженому зростанні числа незалежних спостережень n, імовірність нерівності прямує до границі

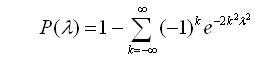
4. Обчислюється величина ;

5. За відповідною таблицею (див. нижче) знаходиться імовірність Р(λ), відповідна тому, що за рахунок випадкових причин максимальні розходження між F^*(x) і F(x) будуть не менше, ніж при практичному спостереженні.

Якщо ймовірність Р(λ) дуже маленька, гіпотеза забраковується; при порівняно великій імовірності Р(λ) гіпотеза вважається сумісною з результатом досліду.

Критерій Колмогорова можна застосовувати тільки у випадку коли розподіл F(x) відомий. Якщо ж невідомо точний вигляд функції F(x), то потрібно застосовувати інші критерії.

Статистика виникла не пізніше XVIII століття. У правителів держав була необхідність збирати дані про свої народи та країни. Її зміст розширився на початку XIX століття і почав включати збір та аналіз даних в цілому. Нині статистичні дані широко застосовуються у сфері управління, бізнесу, природничих та соціальних наук.

Історичний розвиток методів статистичних досліджень.

1) До першого етапу, як уже було згадано, належать методи, описані в Біблії (наприклад книга Чисел, де наводиться число воїнів у різних племенах). З математичної точки зору справа зводилася до підрахунку числа попадання значень спостережуваних ознак у певні градації.

2) Надалі результати обробки статистичних даних стали подавати у вигляді таблиць і діаграм.

3) Математичні основи статистики були закладені в XVII та XVIII століттях паралельно з розвитком теорії ймовірностей. Відразу після виникнення теорії ймовірностей (Паскаль, Ферма, XVII століття) імовірнісні моделі стали використовуватися при обробці статистичних даних. Наприклад, вивчалася частота народження хлопчиків і дівчаток.

П'єр Сімон Лаплас (1774) зробив першу спробу вивести правило поєднання спостережень із принципами теорії ймовірностей. Він показував закони ймовірності помилки на кривій. Лаплас вивів формулу для середньої з трьох спостережень, також дав формулу для закону об'єкта помилки (1781).

4) Метод найменших квадратів було винайдено на рубежі XIX століття кількома авторами. У 1794 р. (за іншими даними - в 1795 р.) К. Гаусс розробив метод найменших квадратів, один з найбільш популярних нині статистичних методів, і застосував його при розрахунку орбіти астероїда Церерра - для боротьби з похибками астрономічних спостережень. З тих пір нові методи теорії ймовірностей і статистики були в постійному розвитку.

5) Сучасний етап розвитку статистичних методів можна відраховувати з 1900 р., коли англієць К. Пірсон заснував журнал «Biometrika». Перша третина ХХ ст. пройшла в напрямку досліджень параметричної статистики. Вивчалися методи, засновані на аналізі даних з параметричних родин розподілів, описуваних кривими сімейства Пірсона. Найбільш поширеним був нормальний (гауссів) розподіл. Для перевірки гіпотез використовувалися критерії Пірсона, Стьюдента, Фішера, Колмогорова. Було запропоновано метод максимальної правдоподібності, дисперсний аналіз, сформульовано основні ідеї планування експерименту.

Отже, статистика як наука була створена, на загальну думку фахівців, порівняно недавно - у першій половині ХХ ст. Саме тоді було розроблено основні ідеї та отримано результати. Починаючи з 70-х років ХХ ст. дослідження з математичної статистики присвячені узагальненню та подальшому математичному вивченню цих завдань. Потік нових математичних результатів (теорем) не слабшає, але нові практичні рекомендації з обробки статистичних даних при цьому не з'являються. Можна сказати, що математична статистика як науковий напрямок замкнулася всередині себе.

Питання для самоперевірки

1. Сформулюйте основні поняття математичної статистики (генеральна і вибіркова сукупності), статистичний ряд (або сукупність), формули і побудови статистичних функцій розподілу.

2. Наведіть формули для статистичних параметрів, їх збіжність до теоретичних параметрів.

3. Означення і одержання формул для довірчого інтервалу і довірчої ймовірності.

4. Сформулюйте основні критерії згоди.

5. Наведіть основні пункти розвитку статистичних досліджень.