Розділ 2 ФОРМИ ПОДАННЯ ФУНКЦІЙ АЛГЕБРИ ЛОГІКИ

Існує багато способів задання логічних функцій. Раніше був розглянутий табличний спосіб, при якому кожному набору значень змінних в таблиці істинності указується значення логічної функції. Цей спосіб наочний і може бути застосований для запису функцій від будь-якої кількості змінних. Проте при аналізі властивостей функцій алгебри логіки (ФАЛ) такий запис не є компактним. Простіше виглядає аналітичний запис у вигляді формул.

Розглянемо функцію, яка подана у вигляді суперпозицій булевої алгебри

          .

Застосовуючи наведені вище тотожності, перетворимо цю функцію

          .

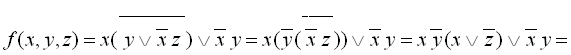
Таким чином, одна і та ж функція може бути подана різними формулами. В зв’язку з цим виникає задача знаходження такої форми запису функцій, при якій кожній функції відповідає одна і лише одна формула, а формулі відповідає одна і лише одна функція.

Такі форми запису називають канонічними.

Канонічні форми запису називаються також досконалими диз’юнктивними нормальними формами (ДДНФ) або досконалими кон’юнктивними нормальними формами (ДКНФ).

     2.1     Досконала диз’юнктивна нормальна форма

Елементарними добутками в алгебрі логіки називають вирази у вигляді , тобто заперечення ставиться тільки над кожною окремою змінною. Диз’юнкція добутків називається диз’юнктивною нормальною формою (ДНФ).

Окрім нормальних диз’юнктивних форм можуть бути і інші диз’юнктивні форми. Наприклад, не можна називати ДНФ, оскільки не є елементарним добутком.

Нехай дано набір змінних . Добуток всіх змінних, взятих з запереченнями або без них, називають конституентами одиниці. Будь-яка конституента дорівнює одиниці лише на одному наборі змінних.

Щоб записати конституенту одиниці n змінних, яка дорівнює одиниці на m-му наборі, потрібно число m подати у вигляді n-розрядного двійкового числа і в добутку взяти з запереченнями ті змінні, яким в двійковому числі відповідають нулі.

Наприклад, конституента одиниці змінних яка дорівнює одиниці на 25-му наборі, має вигляд:

Диз’юнкція конституент одиниці називається досконалою диз’юнктивною нормальною формою.

Будь-яку логічну функцію (окрім константи нуля) можна подати в досконалій диз’юнктивній нормальній формі, яка є єдиною для цієї функції.

На наступному прикладі розглянемо порядок визначення ДДНФ.

Приклад. Подати в ДДНФ логічну функцію п’яти аргументів , яка дорівнює 1 на наборах з номерами 4, 10, 15, 20 і нулю на решті наборів.

Для знаходження ДДНФ виконаємо такі операції:

1. Номери наборів, які набувають значення 1, записуються в двійковому коді, потім подаються у вигляді добутку змінних, в якому над аргументами, які дорівнюють нулю, ставиться знак заперечення.

2. Набори добутків об’єднуються знаком диз’юнкції

          .