3.4 Метод Нельсона
Метод дозволяє отримати скорочену ДНФ булевої функції f з її довільної кон’юнктивної нормальної форми. Суть методу полягає у використанні такого твердження, яке наводимо без доведення [9]: якщо в довільній КНФ булевої функції f розкрити дужки і зробити всі поглинання, то в результаті отримаємо скорочену ДНФ булевої функції f.
Приклад:
Булева функція f задана КНФ:
![]() .
.
Знайти методом Нельсона скорочену ДНФ функції f. Після розкриття дужок отримуємо:
![]() .
.
Після проведення всіх поглинань отримали ![]() . Отримана скорочена ДНФ функції f.
. Отримана скорочена ДНФ функції f.
3.5. Метод карт Карно-Вейча
Одним з способів подання булевих функцій від невеликої кількості змінних є карти Карно. Їх різновид – карти (діаграми) Вейча, які будуються як розгортки кубів на площині. При цьому вершини куба зображуються як клітинки карти, координати яких збігаються з координатами відповідних вершин куба. Карта заповнюється так само, як таблиця істинності: значення 1 вказується в клітинці, що відповідає набору, на якому функція має значення 1. Значення 0 звичайно на картах не відображається.
Карти (діаграми) Вейча
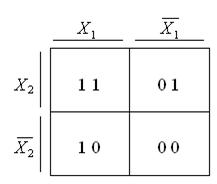
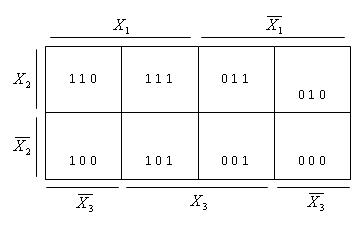
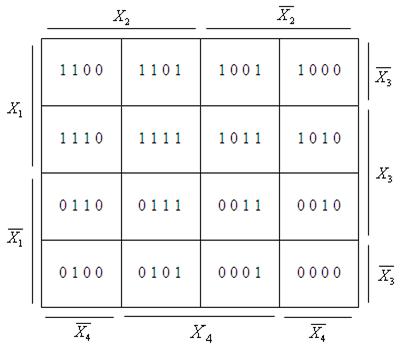
Метод дозволяє швидко одержати мінімальні ДНФ булевої функції ![]() невеликої кількості змінних. В основі методу лежить задання булевих функцій діаграмами деякого спеціального вигляду: їх називають діаграми Вейча. Для булевої функції двох змінних діаграма Вейча має вигляд (таблиця 3.8). Кожна клітинка діаграми відповідає набору змінних булевої функції в її таблиці істинності. В клітинці діаграми Вейча ставиться одиниця, якщо булева функція набуває одиничного значення на відповідному наборі. Нульові значення булевої функції в діаграмі Вейча не проставляються. Для булевої функції трьох змінних діаграма Вейча має такий вигляд (табл. 3.9), аналогічно діаграма Вейча для функції чотирьох змінних має вигляд (табл. 3.10).
невеликої кількості змінних. В основі методу лежить задання булевих функцій діаграмами деякого спеціального вигляду: їх називають діаграми Вейча. Для булевої функції двох змінних діаграма Вейча має вигляд (таблиця 3.8). Кожна клітинка діаграми відповідає набору змінних булевої функції в її таблиці істинності. В клітинці діаграми Вейча ставиться одиниця, якщо булева функція набуває одиничного значення на відповідному наборі. Нульові значення булевої функції в діаграмі Вейча не проставляються. Для булевої функції трьох змінних діаграма Вейча має такий вигляд (табл. 3.9), аналогічно діаграма Вейча для функції чотирьох змінних має вигляд (табл. 3.10).
Таблиця 3.8
Таблиця 3.9
Таблиця 3.10
Правила мінімізації такі:
1. Дві сусідні клітинки (два 0-куби) утворюють один 1-куб. При цьому мається на увазі, що клітинки, які знаходяться на межах карти, також є сусідніми відносно одна одної;
2. Чотири вершини можуть об’єднуватися, утворюючи один 2-куб, що містить дві незалежні координати;
3. Вісім вершин можуть об’єднуватися, утворюючи один 3-куб;
4. Шістнадцять вершин, об’єднуючись, утворюють один 4-куб і т.д.
Відзначимо, що сусідніми клітинками є клітинки, які збігаються при суміщенні карт поворотом навколо загального ребра.
Сукупність прямокутників, які покривають усі одиниці, називається покриттям. Зазначимо, що одна і та ж комірка може покриватися два або декілька разів.
Таким чином, формула, що отримується в результаті мінімізації логічної функції за допомогою діаграм Вейча, містить суму стількох елементарних добутків, скільки прямокутників є в покритті. Чим більше комірок в прямокутнику, тим менше змінних міститься у відповідному йому елементарному добутку.
Нехай задана логічна функція:
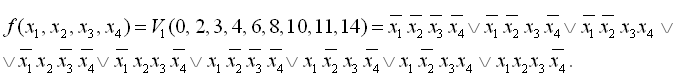
Будуємо діаграму Вейча для заданої функції:
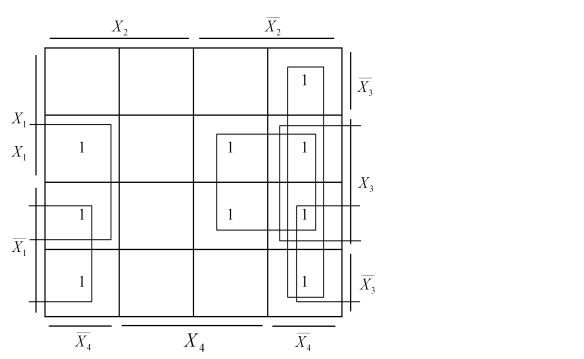
Таким чином, мінімальна форма заданої функції має такий вигляд:
![]() .
.
Карти Карно
Метод карт Карно знаходить широке застосування для мінімізації логічних функцій.
Основою мінімізації за допомогою карти Карно є такий крок: два мінтерма, що знаходяться в сусідніх клітинках карти, можуть бути замінені однією кон’юнкцією, яка містить на одну змінну менше. Якщо сусідніми є дві пари мінтермів, то така група з чотирьох мінтермів може бути замінена кон’юнкцією, яка містить на дві змінних менше. В загальному випадку наявність мінтермів в 2n сусідніх клітинках дозволяє виключити n змінних. Такі дії можливо показати, якщо сусідні пари мінтермів перетворювати методом послідовного виключення змінних, використовуючи при цьому закони
![]()
правила поглинання ![]()
і склеювання 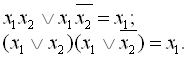
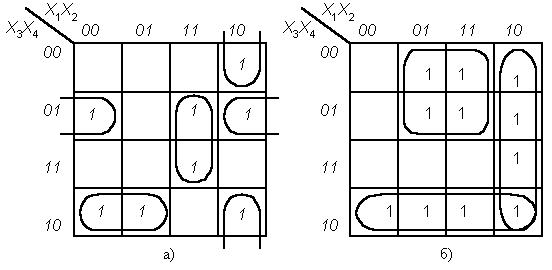
Рисунок 3.2 - Приклади об’єднання клітинок в картах Карно
Виконучи мінімізацію необхідно пам’ятати, що сусідніми клітинками є не тільки клітинки, які розміщені близько по горизонталі і вертикалі, але й клітинки на протилежних сторонах карти Карно; клітинки можуть об’єднуватися по дві (рис. 3.2, а), чотири (рис 3.2, б) і т. ін.; одна і та ж клітинка карти Карно може входити в декілька груп.
Картами Карно можна користуватися для мінімізації логічних функцій, заданих як в ДДНФ, так і в ДКНФ.![]()
Приклад. Логічну функцію
![]()
задану в ДДНФ, мінімізувати за допомогою карти Карно.
Розв’язання. 1. Зобразимо карту Карно для трьох змінних X1, X2, X3 і відмітимо в ній одиничні мінтерми ![]()
![]() ,
, ![]() і
і ![]() (рис 3.3, а).
(рис 3.3, а).
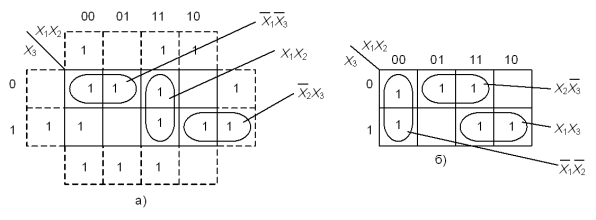
Рисунок 3.3 - Мінімізація логічної функції за допомогою карт Карно
2. В карті Карно (рис. 3.3, а) мінтерми утворюють три групи, кожна з яких містить два мінтерми. Перша складається з ![]() і
і ![]() , з цієї групи
, з цієї групи![]() змінна х2 може бути виключена. Друга група складається з
змінна х2 може бути виключена. Друга група складається з ![]() та
та ![]() і з цієї групи може бути виключена змінна х3. Третя група складається з
і з цієї групи може бути виключена змінна х3. Третя група складається з ![]() і
і ![]() , з якої може бути виключена змінна х1.
, з якої може бути виключена змінна х1.
3. Записуємо мінімізовану логічну функцію в ДНФ:
![]()
Вибираючи групи мінтермів по-іншому (((рис. 3.3, б), отримуємо другу мінімальну форму логічної функції, заданої рівнянням
![]() ,
,
![]()