Варіанти для індивідуальних завдань
Завдання I
Приклади виконання завдання 1:

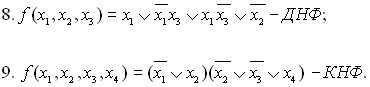 Варіанти завдань:
Варіанти завдань:
1
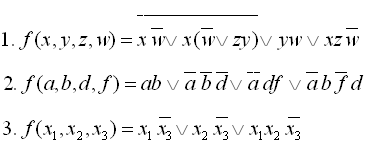

2
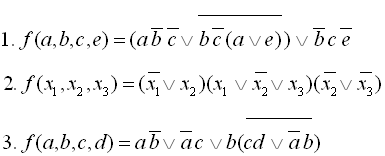
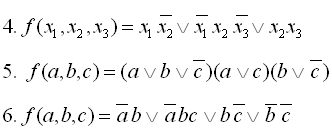
3

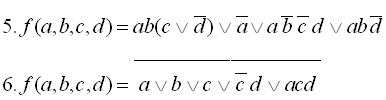 4
4
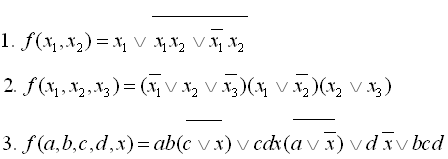
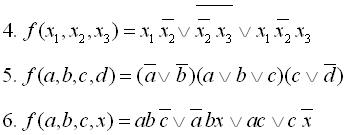
5
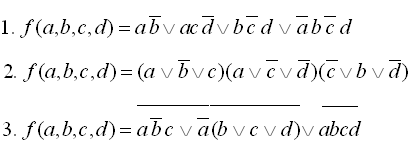
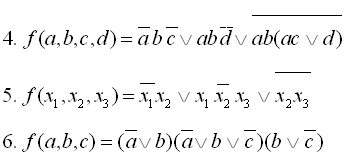
6

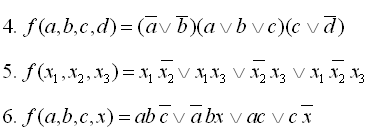
7

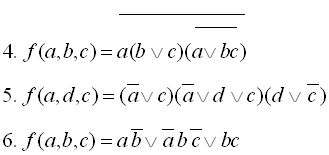
8
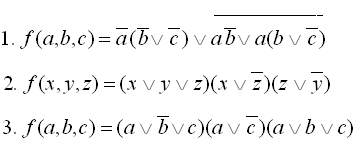
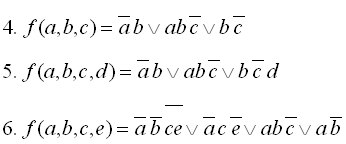
9
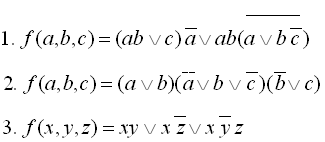

10


11

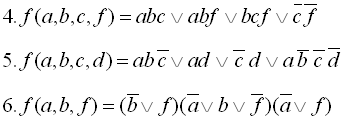
12
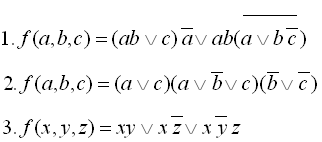
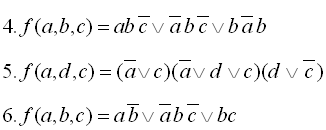
13
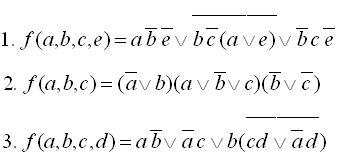

14
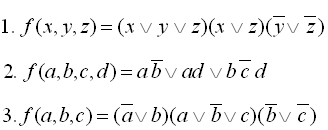
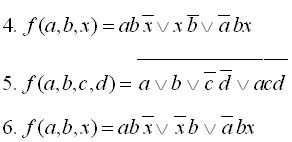
15
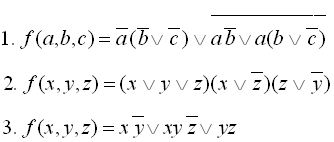
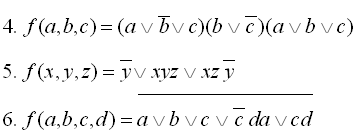
16

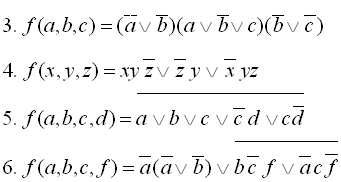
17


18

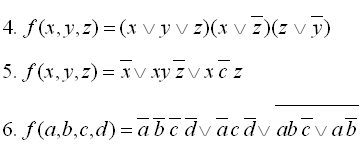
19
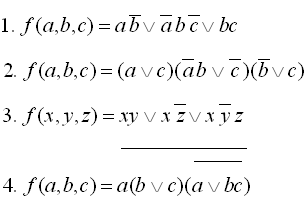
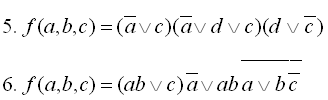
20
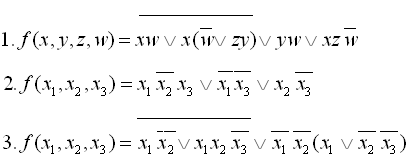
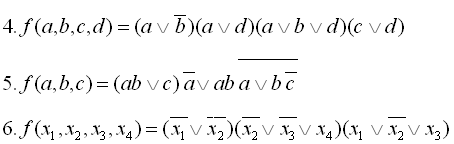
21
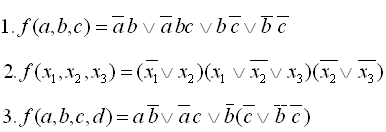
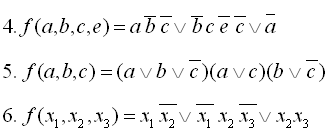
22
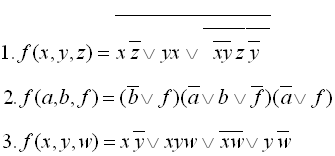
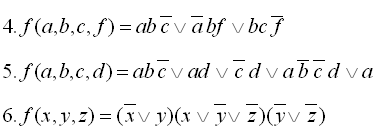
23

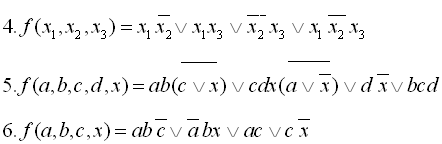
24

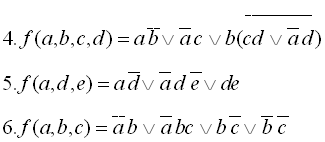
25
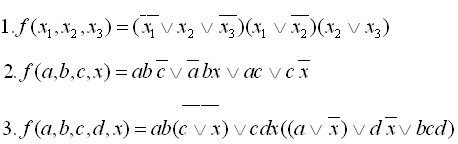

26

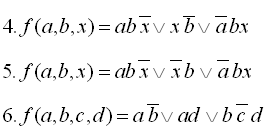
27
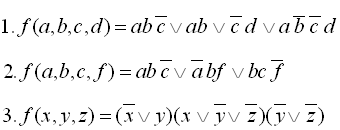
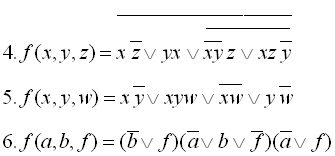
28
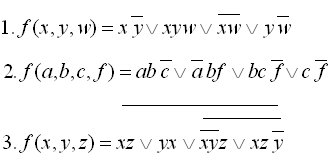
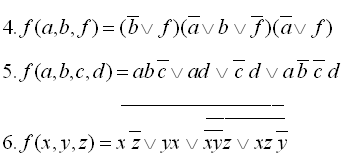
29

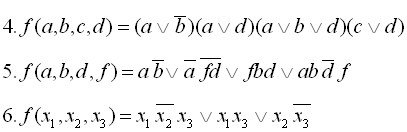
30

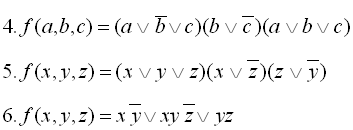
Завдання II
Варіанти завдань
№ варіанта варіант ввваваріанта |
|
№ варіанта |
|
1 |
24 |
33 |
37 |
2 |
48 |
34 |
54 |
3 |
53 |
35 |
25 |
4 |
57 |
36 |
56 |
5 |
38 |
37 |
28 |
6 |
18 |
38 |
12 |
7 |
22 |
39 |
44 |
8 |
40 |
40 |
32 |
9 |
36 |
41 |
30 |
10 |
34 |
42 |
51 |
11 |
39 |
43 |
58 |
12 |
59 |
44 |
0 |
13 |
55 |
45 |
49 |
14 |
35 |
46 |
31 |
15 |
16 |
47 |
26 |
16 |
29 |
48 |
23 |
17 |
11 |
49 |
20 |
18 |
63 |
50 |
10 |
19 |
41 |
51 |
2 |
20 |
27 |
52 |
14 |
21 |
50 |
53 |
3 |
22 |
33 |
54 |
43 |
23 |
15 |
55 |
52 |
24 |
49 |
56 |
8 |
25 |
45 |
57 |
6 |
26 |
47 |
58 |
4 |
27 |
46 |
59 |
5 |
28 |
60 |
60 |
7 |
29 |
21 |
61 |
62 |
30 |
19 |
62 |
9 |
31 |
17 |
63 |
61 |
32 |
42 |
64 |
1 |
Завдання III
Варіанти завдань:
1.
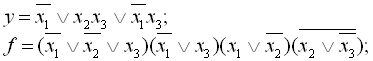
2.
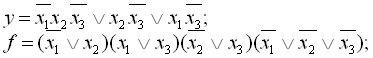
3.
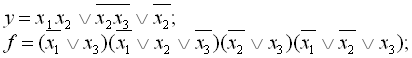
4.
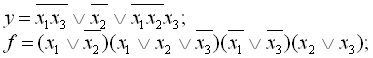
5.
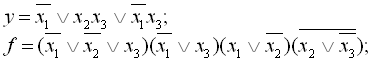
6.
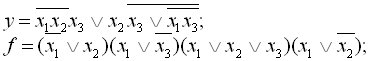
7.
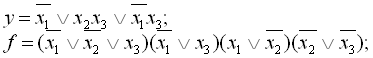
8.

9.

10.
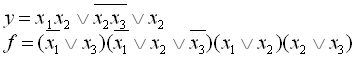
11.
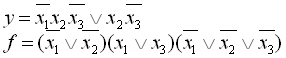
12.
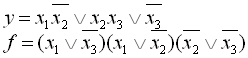
13.
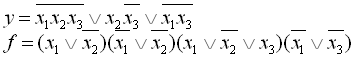
14.
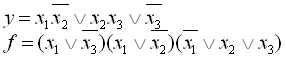
15.
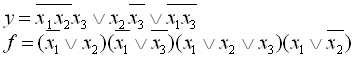
16.
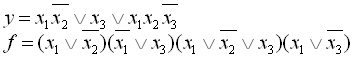
17.

18.
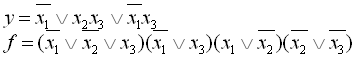
19.

20.
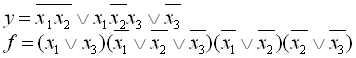
21.
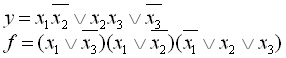
22.
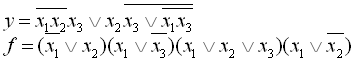
23.
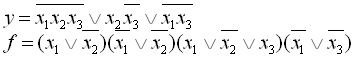
24.

25.
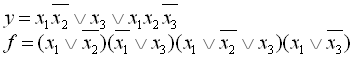
26.

27.
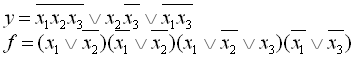
28.
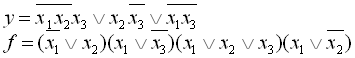
29.
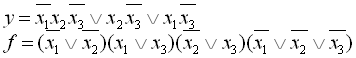
30.

Завдання IV
Варіанти завдань
№ варіанта |
|
|
Набори з номерами |
1 |
|
1 |
0,2,3,5,6 |
2 |
|
1 |
3,6,8,14,12 |
3 |
|
1 |
7,18,20,24,30 |
4 |
|
1 |
2,4,6,9,13 |
5 |
|
1 |
4,6,8,9,14 |
6 |
|
1 |
1,3,6,8,14 |
7 |
|
1 |
6,8,15,19,24 |
8 |
|
1 |
2,6,10,13 |
9 |
|
1 |
0,4,7,8,9 |
10 |
|
1 |
0,2,5,8,11 |
11 |
|
1 |
0,4,5,6 |
12 |
|
1 |
6,7,8,12,14 |
13 |
|
1 |
0,4,8,9,14 |
14 |
|
1 |
0,1,5,8,12 |
15 |
|
1 |
0,4,7,9,14 |
16 |
|
0 |
0,4,7,9,10,14 |
17 |
|
1 |
0,1,3,11,14 |
18 |
|
1 |
5,8,12,17,24 |
19 |
|
1 |
0,1,3,5,7,14 |
20 |
|
0 |
0,1,7,12,13 |
21 |
|
0 |
2,3,10,12 |
22 |
|
0 |
2,4,6,26,27 |
23 |
|
0 |
2,3,8,9,13 |
24 |
|
0 |
0,1,4,5,6 |
25 |
|
0 |
2,3,8,17,26 |
26 |
|
0 |
7,18,20,24,30 |
27 |
|
1 |
1,3,6,13 |
28 |
|
1 |
0,3,11,14 |
29 |
|
1 |
0,2,14,20,29 |
30 |
|
1 |
0,1,3,5,7 |
Завдання V
Приклади розв’язання завдання V.
1. Приклад мінімізації логічної функції за допомогою діаграми Вейча.
Задана функція ![]() , нижче наведено отримання мінімальної функції
, нижче наведено отримання мінімальної функції
Мінімізована функція: ![]() .
.
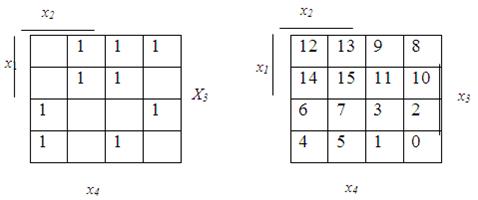
2. Приклад мінімізації логічної функції за допомогою методу Квайна.
Використання методу Квайна для заданої функції:
![]()
 Отримаємо скорочену форму функції:
Отримаємо скорочену форму функції:
![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]()

Fmin=![]() +
+![]() +
+![]() +
+![]() .
.
3. Приклад мінімізації логічної функції за допомогою методу
діаграм Вейча, Квайна-Мак-Класкі
F(x1,x2, x3, x4)=V1(2, 4, 5, 7, 9, 11, 13, 15)
Діаграми Вейча
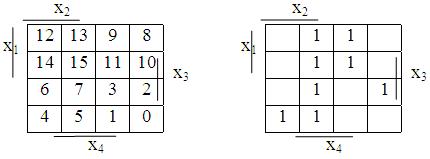
![]()
![]()
![]()
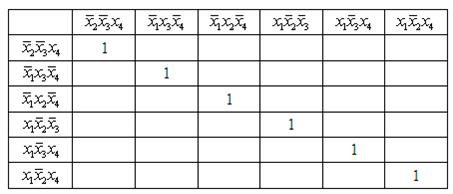
Метод Квайна-Мак-Класкі
K0={0010, 0100, 0101, 0111, 1001, 1011, 1101, 1111}.
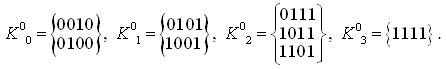
1. Знаходження первинних імплікант:
а) порівняння ![]() і
і ![]()
0010 0101* ![]()
0100* 1001
б) порівняння ![]() і
і ![]()
0101* 0111* 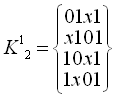
1001* 1011*
1101*
в) порівняння ![]() і
і ![]()
0111*
1011* 1111* 
1101*
г) розбиття на групи
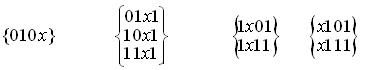
д) порівняння всередині кожної групи
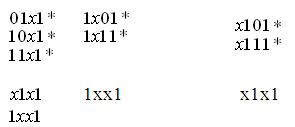
2. Будуємо таблицю покриття:
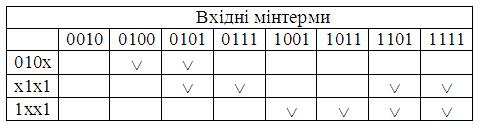
![]() .
.
Метод Квайна
![]()
![]()
1. Знаходження первинних імплікант
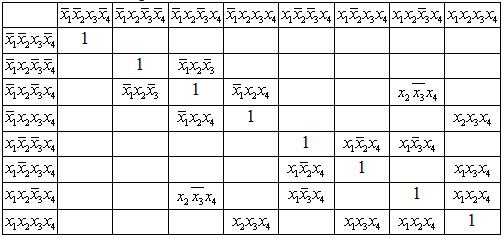
2. Знаходження простих імплікант

3. Будуємо таблицю покриття
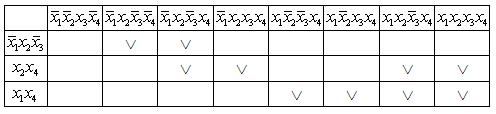
![]() .
.
Варіанти завдань
|
22. V1(0,1,4,7,11,12,15) |
1. V1(0,2,3,5,7,8,10,13) |
23. V1(1,2, 6,7,9,10,11,13) |
2. V1(0,1,2,3,4,9,10,11,12) |
24. V1(2,3,5,7,9,11,12,14) |
3. V1(0,1,2,4,6,9,8,11) |
25. V1(0,1,2,4,5,8,11,12,15) |
4. V1(0,1,3,5,7,9,10,14) |
26. V1(1,2,4,6,10,11,15) |
5. V1(1,2,5,6,8,9,11,13,14) |
27. V1(2,4,5,7,9,11,13,14) |
6. V1(1,3,4,7,9,12,13) |
28. V1(1,6,7,9,10,11,14,15) |
7. V1(0,1,2,5,7,8,11,14,15) |
29. V1(2,3,4,10,11,12,14) |
8. V1(1,2,3,5,8,9,10,11) |
30. V1(0,2,4,5,6,8,12,14) |
9. V1(0,1,3,4,6,8,10,12) |
31. V1(1,3,6,8,11,12,13,15) |
10. V1(1,4,5,9,11,12,13,14) |
32. V1(1,5,6,7,9,10,13,14) |
11. V1(1,3,5,9,11,13,14) |
33. V1(2,4,6,7,11,12,13,14) |
12. V1(0,1,2,8,9,10,11,14) |
34. V1(0,3,7, 9,10,11,12,14) |
13. V1(0,1,2,5,6,8,10,15) |
35. V1(0,2,6,7,10,12,13) |
14. V1(0,1,4,7,8,11,12,14) |
36.V1(1,4,6,7,9,11,13,14,15) |
15. V1(1,4,6,7,10,11,13,15) |
37. V1(0,3,5,7,9,10,11,14) |
16. V1(0,2,4,5,6,9,10,12) |
38. V1(0,1,4,5,7,12,13,15) |
17. V1(2,4,6,8,11,12,13,15) |
39. V1(0,2,4,5,7,11,12,13,15) |
18. V1(1,4,5,10,11,12,13,15) |
40. V1(0,1,4,5,6,8,10,11,13) |
19. V1(0,2,3,6,8,10,11,14) |
41. V1(1,2,3,4,5,7,8,9,13) |
20. V1(0,1,2,5,6,9,11,13) |
42. V1(0,1,2,4,5,7,8,9,11) |
21. V1(1,2,5,7,10,13,15) |
43. V1(0,3,4,7,9,11,12,14,15) |
44. V1(3,4,7,9,10,12,14,15) |
45. V1(0,1,2,4,6,8,9,11,12) |