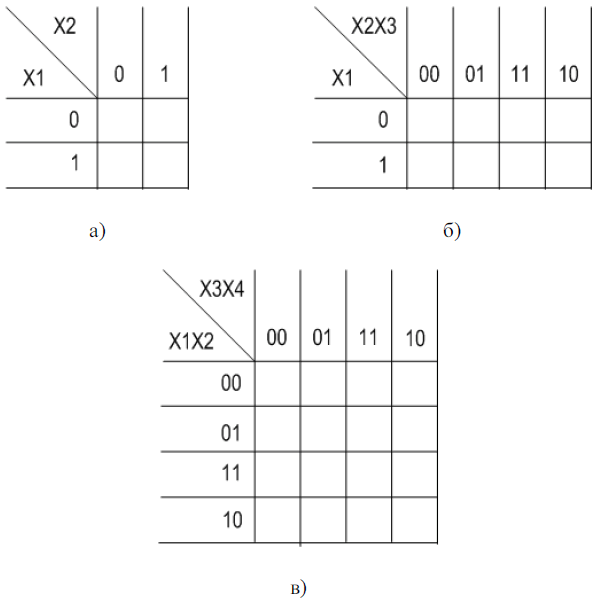
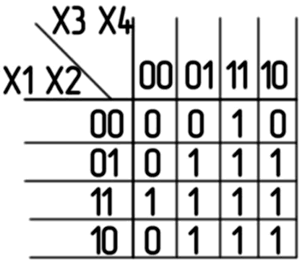
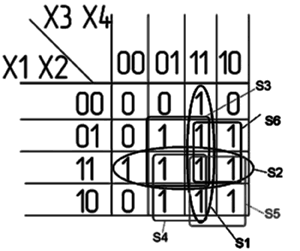
Аналіз і синтез комбінаційних схем

Мета: отримати навички аналізу і синтезу комбінаційних схем.

4.1 Теоретичні відомості

Для складання схеми електричної функціональної необхідно, вирішити задачу написання системи власних функцій або функцій, що відображають логіку роботи цієї схеми і мають однозначний розв'язок. Для цього необхідно скласти таблицю істинності, в якій вказати значення функції залежно від комбінації вхідних сигналів.

Синтез полягає в побудові функціональної електричної схеми за мінімізованою функцією (найчастіше в єдиному базисі І–НІ, АБО–НІ).

Для розроблення необхідного цифрового пристрою на основі таблиці істинності записують його логічний вираз. Потім з метою спрощення цифрового пристрою проводять мінімізацію логічного виразу і розроблення схеми, що реалізує отриманий логічний вираз.

Досконалу диз'юнктивну нормальну форму (ДЗНФ) подають добутком груп. Кожну групу складено з суми, в яку входять всі змінні.

Якщо схема має декілька виходів, то кожен вихід описано своєю функцією. Таку систему функцій названо системою власних функцій, що складена на основі таблиці істинності (табл. 4.1) за таким правилом: для кожного набору змінних, при якому функція дорівнює 1, записана як добуток, в якому із запереченням беруться змінні, що мають значення 0.

(4.1)

Досконалу кон'юнктивну нормальну форму (ДКНФ) складають на основі таблиці істинності (див. табл. 4.1) за правилом: для кожного набору

змінних, при якому функція дорівнює 0, записана як сума, в якій з інверсією беруться змінні, що мають значення 1.

(4.2)

Для мінімізації потрібно функцію привести до досконалої диз'юнктивної нормальної форми, після чого заповнити діаграму Вейча (карти Карно) для n змінних. При цьому у відповідну клітинку діаграми вписати 1, якщо функція при даному наборі аргументів дорівнює одиниці. У решту клітинок вписати нулі або такі клітинки взагалі залишити порожніми.

В карту Карно булеві змінні передаються з таблиці істинності і впорядковуються за допомогою коду Грея, в якому кожне наступне число відмінне від попереднього тільки одним розрядом (див. рис. 4.1).

Для прикладу розглянуто випадок, коли таблиця подана чотирма змінними і заповнимо її у відповідності із наведеними правилами.

У заповненій діаграмі обводяться прямокутними контурами клітинки з одиницями, після чого було записано мінімізовану функцію у вигляді диз'юнкції простих імплікантів, що описують ці контури. При проведенні контурів дотримуються таких правил:

- усередині контуру мають бути тільки клітинки з одиницями;

- кількість клітинок з одиницями повинна виражатися величиною 2×i (де i = 0, 1,2 ...), тобто може дорівнювати 1, 2, 4, 8 і т. д.;

- одиниці в крайніх клітинках одного стовпця або одного рядка можуть включатися в один контур; кожен контур повинен включати як можна більше число клітинок з одиницями, а спільне число контурів має бути якомога меншим.

В результаті мінімізації отримана ДЗНФ такого вигляду:

(4.3)

4.2 Порядок виконання роботи

1. Відповідно до таблиці станів отримати ДЗНФ і ДКНФ.

2. Мінімізувати ДЗНФ та ДКНФ за допомогою карт Карно.

3. Побудувати схему на основі базисних елементів для отриманої мінізованої ДЗНФ, ДКНФ.

4. Визначити критерії мінімізації як загальне число різних елементарних кон'юнкцій в отриманій системі.

5. Порівняти значення критеріїв.

4.3 Зміст звіту

1. Мета та цілі роботи.

2. Розрахункова частина. (Основні розрахункові формули та розрахунок)

3. Програма, написана мовою програмування (C++, C# , Pascal), що виконує задачу поставлену у лабораторній роботі.

4. Висновки.

4.4 Контрольні питання

1. Принципи формування ДЗНФ.

2. Принципи формування ДКНФ.

3. Як передаються булеві змінні з таблиці істинності в карту Карно?

4. Які основні правила при проведенні контурів?

5. Розрахуйте ефективність оптимізації за допомогою карт Карно.

4.5 Варіанти завдань