2. Процедури машинної графіки

2.4. Алгоритми заповнення областей, обмежених полігонами

Однією з найбільш поширених задач машинної графіки є задача визначення і заповнення внутрішньої частини контуру.

Процедура заповнення полягає у визначенні адрес всіх внутрішніх точок області, обмеженої контуром і у встановлені її відповідним пікселам заданого кольору, тобто по визначеним адресам в відеопам'ять записують код кольору.

Заповнення проводять під кутами, кратними 45°, оскільки тільки в цьому випадку будуть відсутні “точки-просікання”. Останні мають місце за рахунок зміщення початку вектору, що приводить до пропуску точок області при формуванні діагональних кроків (див. рис.2.6.). 

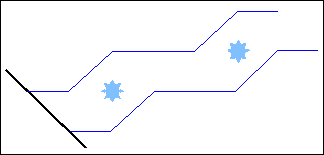
Рис. 2.6. Поява точок-просікання

Задачу заповнення розв'язують різними способами, які поділяють на два великих класи.

Перший з них передбачає наявність точного опису контуру. При цьому визначення частин площини, які лежать у середині області, базується на аналізі рівнянь, які задають відповідні лінії. Методи другого класу передбачають відображення заповнюваного контуру на дискретну площину і визначення внутрішньої частини області на основі значень яскравості пікселів. 

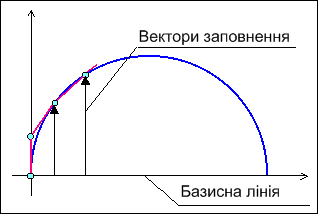
Рис. 2.7. Заповнення області, обмеженої контуром, по мірі його формування

Заповнення області по мірі формування контуру, який її обмежує, полягає в слідуючому (рис.2.7):

1.  Проводять умовну базисну лінію, яка, як правило, поділяє область на 2 частини.

2.  Формують точки траєкторії контуру до появи крокового приросту в напрямку базисної лінії.

3.  Від базисної лінії проводять вертикальний (горизонтальний) вектор до визначеної точки траєкторії (можливе також заповнення вектором з кутом нахилу45^о). Для кожної точки вектора встановлюють колір.

4.  Дії 2-3 повторюють до заповнення першої частини області.

5.  Дії 2-4 виконують для нижньої частини контуру.

Безумовно, що базисна лінія може мати любу форму або нахил, але найбільш доцільно використовувати для цього горизонтальний або вертикальний вектор, оскільки в цьому випадку обчислювальні затрати будуть найменші.

Методи заповнення можна поділити в залежності від того, який принцип застосовується для встановлення внутрішніх точок багатокутника. У деяких алгоритмах застосовується перевірка на парність, в інших критерій зв'язності.

Алгоритми заповнення області, в яких застосовують перевірку на парність, базуються на тому, що довільна пряма перетинає будь-яку замкнену криву парну кількість разів. Якщо відомо, що перша точка відповідної лінії лежить за контуром, то, виконавши обхід цієї лінії, шляхом відрахувань кількості перетинів можна встановити, які саме її відрізки розміщені в області. Якщо число перетинів непарне, то відповідний відрізок розміщений у внутрішній області (відрізки AB і CD на рис.2.8), в іншому випадку - поза областю (відрізок BC). 

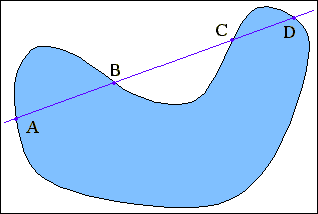
Рис. 2.8. Визначення границі контура по критерію парності

Як правило, вводять допоміжну змінну з нульовим початковим станом. При кожному перетину контуру скануючим відрізком прямої стан змінної міняють на протилежний ( рис. 2.9 ). 

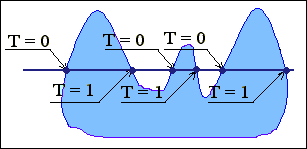
Рис. 2.9. Формування станів змінної Т при скануванні області.

В разі, коли скануючий відрізок прямої є дотичним до контуру, алгоритм не дає правильний результат, оскільки дотик може здійснюватись кількома точками. Останнє вказує на необхідність виявлення точок-дотику.

У цьому випадку можна виконувати аналіз за двома допоміжними прямими ДП1 і ДП2 (рис.2.10), розміщеними над і під скануючим відрізком ОП, який використовують для перевірки на парність. Якщо одна з цих прямих не перетинає контур біля точки перетину, це означає, що відрізок ОП є дотичним. 

Рис. 2.10. Визначення наявності дотичних до контуру

Визначити критичні ситуації можливо також за кількістю перетинів скануючого відрізка прямої з контуром ( рис.2.11). Якщо кількість перетинів l для сусідніх рядків не співпадає, то необхідно виконати додатковий аналіз на предмет обробки нештатної ситуації. 

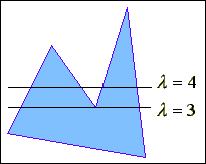
Рис. 2.11. Визначення критичних ситуацій за кількістю перетинів контура зі скануючим відрізком прямої.

Розглянемо метод і відповідний йому алгоритм заповнення області, обмеженої сторонами багатокутника, що використовує принцип парності. Будемо вважати, що сторони багатокутника задані координатами вершин багатокутника х_i, у_i, яким відповідає максимальне значення у або мінімальне значення х, якщо сторона горизонтальна, а також прирости Dx, Dу для визначення координат іншої вершини.

Першим кроком алгоритму є сортування сторін відповідно до максимальних значень у_i, а при їхній рівності по мінімуму х_i. У випадку рівності іх_i використовуються значення Dх, а потім Dу. При цьому вибирається сторона з найменшим алгебраїчним значенням. У результаті одержуємо упорядкований список сторін контуру - список черговості.

Другий крок алгоритму виконується для всіх суміжних сторін списку з однаковими значеннями y, що відповідає локальному максимуму. Через вершину багатокутника, що відповідає цим сторонам, проводиться пряма, паралельна осі X, і визначаються точки її перетину з іншими сторонами, що розташовані в списку вище проаналізованих. Дані прямі поділяють контур на прошарки, що містять парне число меж. Кожному прошарку відповідає спеціальний список, названий поточним, що містить межі. Для формування поточного списку список черговості включає мітки трьох типів.

Мітка M1 визначає число меж, переданих із списку черговості в поточний список: дві - якщо точки відповідає максимуму; одна - якщо вона не є максимумом; більш двох, якщо одному значенню у відповідає більш одного максимуму.

Мітка М2 служить для введення в поточний список наступної пари меж при переході в наступний прошарок. Її значення відповідає значенню y, при котрому цей перехід повинний відбутися. Зазначеними мітками мітять перші сторони зі списку черговості, із якими перетинаються прямі, проведені через вершини багатокутника, що є локальними максимумами. 

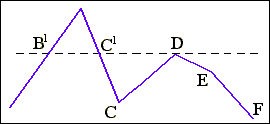
Рис. 2.12. Формування списку черговості. 

Мітка М3 визначає число нових меж, до яких провадиться звертання при завершенні роботи з поточною межею. Табл. ілюструє формування списку черговості і міток для одержання поточного списку на прикладі фрагмента області, приведеної на рис. 2.12.

Таблица 2.1. Опис меж

Третім кроком алгоритму є безпосереднє заповнення області послідовно для кожного прошарку. Цей процес починається з першої пари меж списку черговості шляхом формування і обновлення поточного списку, використовуючи наявні мітки, що дозволяють видаляти і включати нові межі. Організація поточного списку дає можливість реалізувати для кожного прошарку принцип парності, у зв'язку з тим, що всі локальні максимуми визначені. Необхідно відзначити, що приведений алгоритм не враховує наявність горизонтальних сторін багатокутника. Проте модифікація алгоритму для урахування цих ситуацій не має істотних трудностей.

Заповнення області за критерієм зв'язності вимагає наявності піксела-затравки, який розміщений всередині контуру.

Для його завдання існує декілька засобів. У ряді режимів він може бути заданий оператором. У інших випадках у якості затравочного піксела можна взяти точку, безпосередньо суміжну з пікселем контуру. Що стосується завдання контуру, то він, як правило, визначається сукупністю точок поелементного еквівалента зображення. У випадку завдання контуру багатокутником попередньо здійснюється процедура одержання його поелементного еквівалента за допомогою генератора векторів. Будемо вважати, що контур та затравочний піксел згенеровані.

Найпростіший рекурсивний алгоритм полягає в розгляді чотирьох сусідніх до затравочного піксела елементів на предмет їхньої приналежності контуру (рис. 2.13 ). Піксели, що не належать контуру, у свою чергу можуть використовуватися в якості затравочних. 

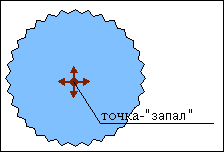
Рис. 2.13. Заповнення області рекурсивним алгоритмом. 

Розглянутий алгоритм при своїй зовнішній простоті потребує значного обсягу обчислень. Це пов'язано в першу чергу з дублюванням розгляду сусідніх елементів для сусідніх затравочних пікселей.

Альтернативний нерекурсивний алгоритм полягає в наступному. Починаючи з затравочного піксела( рис. 2.14.) проводиться аналіз на приналежність пікселей контуру, що знаходяться вліво, а потім управо від затравочного з одночасним зафарбуванням. Далі здійснюється перехід на нижню сторону з повторенням процедури. Цей процес продовжується до повного заповнення нижньої від затравочного піксела частини області. Потім проводиться заповнення верхньої частини області.

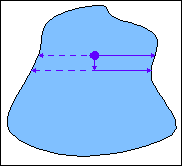
Рис. 2.14. Заповнення області, обмеженої контуром по критерію

У випадку заповнення невипуклих областей необхідно реалізувати стек, у якому будуть зберігатися піксели, розташовані поблизу максимумів і мінімумів контуру. Зазначені піксели використовуються в якості затравочних, послідовно зчитуються зі стека. Очевидно, що задача обчислення цих пікселей не складає особливих проблем.

На рис. 2.15 приведений приклад завдання кількох затравочних пікселів для невипуклих контурів. 

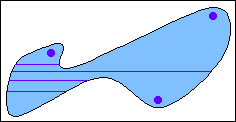
Завдання точок –“затравок” для невипуклого контуру

Контрольні   запитання.

1.  В чому причина появи точок-просікання ?

2.  Як знаходять дотичні до контуру ?

3.  Порівняйте швидкодію алгоритмів по критерію зв'язності та парності.

4.  В яких випадках необхідно декілька точок-затравлення?

     Зміст