4. Методи побудови реалістичних трьохвимірних зображень
4.5. Видалення невидимих частин зображень
Для формування об'ємних зображень використовуються каркасний, контурний і напівтонових методи.
У каркасних конструкціях (ріс.4.11) видимими є всі лінії конструкції. Об'ємність зображеного простору засноване на перспективному ефекті, що створює ілюзію глибини зображення. Реалізація методу вимагає найменших обчислювальних витрат, однак прийнятна тільки для відносно нескладних конструкцій, оскільки наочність зображення падає з збільшенням числа граней.

Рис.
4.11. Каркасна модель.
Рис.
4.12. Контурна модель.
Реалістичність зображень можна істотно підвищити шляхом видалення невидимих ліній і поверхонь. У цьому випадку не зображуються лінії або відрізки ліній об'єктів, закриті їх поверхнями або поверхнями інших об'єктів.
У контурному (рис.4.12) і напівтонових методи (рис.4.13) проводиться видалення ліній, відрізків прямих і граней об'єктів, закритих їх поверхнями або поверхнями інших об'єктів.

Рис.
4.13.
Напівтонових модель з видаленням невидимих частин зображення
Видалення невидимих ліній і поверхонь вважається класичною завданням машинної графіки. До теперішнього часу розроблено велику кількість таких алгоритмів. Серед безлічі алгоритмів видалення невидимих ліній і поверхонь не можна виділити найкращий чи універсальний, придатний для різних застосувань. Вибір конкретного алгоритму залежить від ряду чинників: від прийнятої моделі опису зображуваних об'єктів, виду зображень, необхідної точності подання об'єкта, обмежень на обсяг обчислень і пам'ять.
Видалення невидимих ліній і поверхонь вимагає істотних обчислювальних витрат. Для спрощення використовують ряд спрощень, до числа яких відносять:
* Викреслювання тільки контурів граней об'єктів;
* Апроксимацію контурів ламаною лінією;
* Використання тільки плоских граней.
Завдання видалення невидимих частин зображення значно спрощується, якщо використовувати ортогональне проектування. При центральному проектуванні необхідно визначати точки перетину граней об'єкта з променями, що виходять із точки спостереження, що вимагає додаткових обчислень.
Видалення невидимих ліній використовують в основному при каркасному поданні об'єктів, а поверхонь при контурному і напівтонових.
В алгоритмі Галімберті і Монтанарі, який відноситься до історично першим алгоритмам видалення невидимих ліній, зіставляти положення кожного ребра сцени зі всіма гранями сцени, тобто при видаленні невидимих ліній використовувався чисто геометричний підхід.
Основна ідея алгоритму Варнока полягає в тому, що для аналізу видимості або невидимості елементів зображення здійснюється послідовне розбиття об'єктного простору на складові частини. При такому підході з кожної итерацией завдання видалення невидимих елементів сцени спрощується.
В алгоритмі виділяють ряд стандартних ситуацій для різних випадків взаємних розташувань граней об'єкта, при якому видалення невидимих частин вирішуваний. Об'єктне простір умовно просікати прямокутної трубою. Якщо сцена, укладена в трубу, не належить ні до однієї з стандартних ситуацій, то трубу ділять на чотири підпростори з перерізами, що представляють собою чотири частини вихідного перерізу і проводить їх зіставлення зі стандартними ситуаціями. Безумовно, що при поступовому зменшенні перерізу розглянутих підпросторів ймовірність зустріти таку ситуацію зростає. У найгіршому випадку поділ виконують до однієї точки.
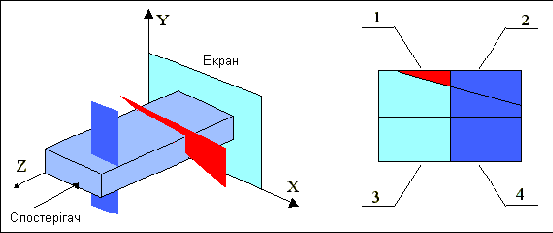
Принцип алгоритму Варнока
На рис. 4.14 показаний приклад виконання однієї ітерації алгоритму Варнока.
Будемо вважати, що отримане розтин не належить до встановлених стандартним ситуацій, тому роблять його поділ на 4 частини (у загальному випадку розбиття можна робити на будь-яке число).
Оскільки подокно 3 порожньо, то воно зображується на екрані фонової інтенсивністю. Аналогічно, подокно 4 повністю "просікати" тільки одну грань об'єкта, тому воно зображується на екрані кольором цієї межі.
У подокне 1 знаходиться тільки один багатокутник, отже він є видимим. Площа поза цим багатокутника заповнюється фоновим значенням інтенсивності, а сам багатокутник - кольором відповідної йому межі.
Розтин в подокне 2 містить дві грані, отже, його необхідно розділити на 4 частини і виконати описані вище дії.
Кількість ітерацій алгоритму Варнока прямо пропорційно насиченості зображення.
Зі збільшенням числа стандартних ситуацій кількість поділів на підпростори зменшується.
Алгоритм Варнока можна використовувати для отримання як векторних, так і растрових зображень.
Ефективність алгоритмів видалення невидимих ліній істотно підвищується, якщо виконати сортування граней об'єктів сцени за їх відстані від точки спостереження. Кінцевим результатом такої сортування є список елементів сцени, впорядкованих за пріоритетом глибини, заснованому на відстані від точки спостереження. Елементи зображення записуються в відеопам'ять починаючи від найбільш віддаленого від точки спостереження. Більш близькі до спостерігача елементи будуть затирати інформацію про більш далеких елементах в буфері.
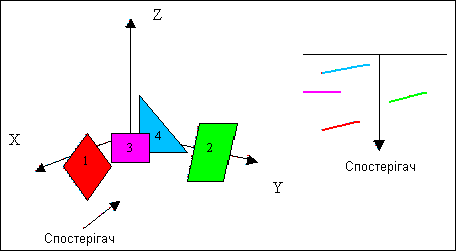
Рис. 4.15. Принцип видалення невидимих граней шляхом сортування по глибині
Розглянемо для прикладу сцену, яка складається з чотирьох граней (ріс.4.15). Нехай грань під номером 4 найбільш віддалена від спостерігача, а грань під номером 1 знаходиться найближче до спостерігача. Висновок проводиться з грані, яка найбільш віддалена (у нашому прикладі це грань 4). Потім виводяться по черзі межі 3, 2, 1.
При реалізації алгоритму необхідно враховувати прозорість граней.
Можливі випадки, коли нова грань не перекриває попередню грань або нова грань частково або повністю перекриває попередню грань.
При варіанті, коли грань не перекривається іншими гранями, вона виводиться без зміни (у прикладі це грань під номером 2). Коли нова грань частково або повністю перекриває попередню грань, то для формування зображення замінюється загальна частина (у разі коли нова грань непрозора), або здійснюється комбінування кольорів (у випадку якщо нова грань прозора).
Алгоритм забезпечує формування реалістичних сцен за рахунок можливості комбінування квітів у кожній точці зображення.
В алгоритмі Уоткінса тривимірна завдання видалення невидимих ліній і поверхонь зводиться до двомірної. Для цього здійснюється розсічення сцени площинами, перпендикулярними поверхні екрану, і виконується аналіз отриманих в перерізі проекцій. Алгоритм виконується по рядках розгортки екрану. Площині перетину називають площинами розгортки.
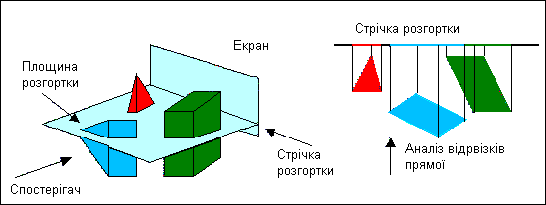
Рис.
4.16. Принцип алгоритму Уоткінса
Зображення в площинах розгортки мають вигляд набору відрізків прямих, що представляють собою ортогональні проекції плоских граней тривимірних об'єктів. Для формування зображення в кожній площині розгортки проводиться аналіз відрізків прямих і визначають їх положення відносно спостерігача. Завдання видалення невидимих граней зводиться до задачі про те, який відрізок бачимо для кожної точки скануючої рядка. Відрізки розташовані ближче до спостерігача, закривають повністю або частково відрізки, розташовані позаду (рис.4.16).
Відомі ряд підходів до прискорення алгоритму. Згідно одного з них визначається видимість відрізків на кожному з інтервалів, отриманих шляхом ділення рядка сканування проекціями точок перетину ребер.
Алгоритм Уоткінса одним з перших був реалізований апаратно.
Метод трасування променів, розроблений на початку 80-х років, дозволяє отримувати найбільш реалістичні зображення шляхом моделювання прозорості, відображення, заломлення і інших оптичних ефектів.
Основна ідея методу полягає в наступному.
Світло, що випромінюється деяким джерелом світла, досягає спостерігача, якщо він відбивається від певній поверхні, переломити або пройшовши через неї. За результатами розрахунку інтенсивності світла, який досягає спостерігача, можна визначити невидимі поверхні (світло не досягає спостерігача) або визначити ступінь прозорості об'єкта, визначивши різницю інтенсивностей світла від джерела і інтенсивності світла, що досяг спостерігача. Однак повний розрахунок променів, що виходять з усіх джерел, званий прямий трасуванням (raytracing), з-за величезної кількості застосовується досить рідко. Крім того, велика частина роботи на відстеження променів, що не потрапили в око спостерігача і на визначення освітленості невидимих поверхонь виявиться проведеної даремно.
Для зниження обчислювальних витрат відстежують промені у зворотному напрямку (raycasting), тобто від спостерігача до об'єкта, як показано на рис.4.17. За перетину променів трасування і об'єктів визначають видимі поверхні.
Джерело світла знаходиться у нескінченності на осі z, тому всі промені, що виходять з нього, паралельні осі z. Кожному променю, що виходить з джерела світла, відповідає свій піксель на екрані. Промені проводяться від спостерігача через гіпотетичну растрову сітку екрану і далі в відображуване простір. Траєкторія кожного променя відстежується, щоб визначити, які саме об'єкти зображення, якщо такі існують, вона перетинає. Необхідно перевірити перетин кожного такого променя з кожним об'єктом зображення. Якщо промінь перетинає об'єкт, то визначаються всі можливі точки перетину променя і об'єкта. Всі точки перетину впорядковуються по глибині. Точка перетину з максимальним значенням глибини представляє видиму поверхню для відповідного пікселя. Якщо ні одна з поверхонь не була пересічена променем, то пикселя присвоюється колір фону.
Значення інтенсивностей променів, Трасувати через всі вузли растрової сітки, розраховуються для трьох колірних складових R, G, B і заносяться до кадрового буфер, звідки виводяться на екран.
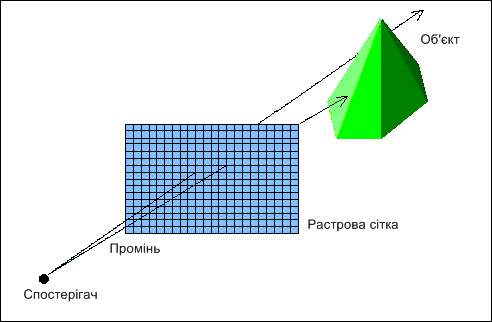
Рис.
4.17. Принцип алгоритму трасування променів
Оскільки 75-95% часу, що витрачається алгоритмом трасування променів, використовується на визначення перетинів променя трасування з об'єктом, то прагнуть зменшити обчислювальну складність цієї процедури. Наприклад, реальні об'єкти умовно поміщають в прості оболонки (паралелепіпед або сферу) і шукають перетин променя з оболонкою (рис.4.18).
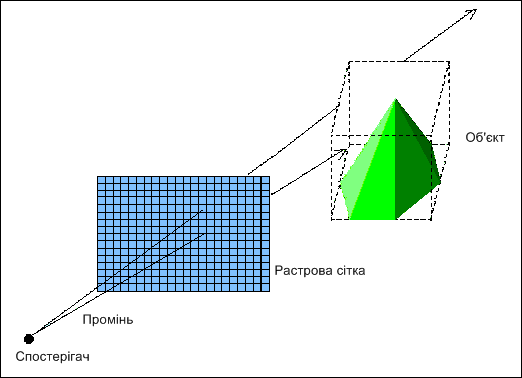
Рис.
4.18.
Розміщення об'єктів в оболонку в алгоритмі трасування променів.
Якщо промінь не перетинає оболонку, то отже, не перетинає і сам об'єкт. Безумовно, що завдання граней оболонки істотно простіше, ніж граней самого об'єкта.
Максимальна "глибина" трасування променів або задається користувачем, або визначається самою програмою-трассировщикам залежно від наявності вільної пам'яті.
Алгоритм трасування променів вимагає великого обсягу обчислень, однак схемотехнічних і алгоритмічна простота трасування променів, можливість виконання незалежних паралельних обчислень для всіх елементів зображення, одержання реалістичних зображень із заданими оптичними властивостями визначають досить широке його використання.
У графічних акселераторах найбільшого розповсюдження отримав алгоритм видалення невидимих поверхонь з використанням Z-буфера. Для реалізації алгоритму окрім традиційної відеопам'яті для зберігання кадру зображення використовують двовимірний масив пам'яті для зберігання глибини (Z-координати) кожного відомого елемента зображення.
При розкладання в растр елементів зображення обчислюється значення глибини Z для кожної точки. Якщо значення глибини Z поточної точки зображення менше ніж значення Z точки, яка раніше зберігалася в відеопам'яті за відповідною адресою, то в відеопам'ять заносять значення поточної точки, а в Z-буфер її глибину. У цьому випадку поточний елемент зображення перекриває вихідний. В іншому випадку модифікація відеопам'яті і Z-буфера не виконується.
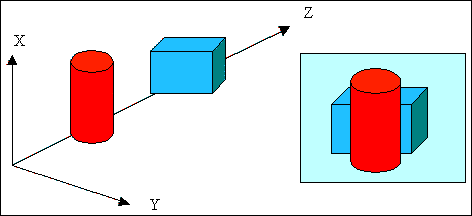
Рис.
4.19. Принцип алгоритму з використанням Z-буфера
Для реалізації високоякісного рендеринга потрібна велика розрядність Z-буфера. Чим вище роздільна здатність завдання глибини, тим вище дискретність z-координат і точніше виконується рендеринг вилучених об'єктів. 24-розрядний z-буфер забезпечує більше 16,7 млн. рівнів завдання глибини, 32-розрядний - більше 2,8 млрд., а 16-розрядний - тільки 65536. Якщо при рендеринга роздільної здатності не вистачає, то може статися, що два перекриваються об'єкта отримають одну і ту ж z-координату, в результаті не буде встановлено, який об'єкт ближче до спостерігача, що може викликати артефакт, званий triangle
disposition.
У сучасних графічних акселераторах використовують виділений для Z-буфера блок пам'яті. У деяких акселераторах для здешевлення конструкції для цієї функції використовують основний буфер, що безумовно позначається на продуктивності.
Z-aлгоритм має просту апаратну реалізацію, не вимагає попередньо сортування примітивів, робить тривіальної візуалізацію перетинів складних поверхонь. Недоліки алгоритму полягають у необхідності введення додаткового обсягу пам'яті, а також в складності реалізації ефектів прозорості та просвеченія. Скрутно усунення сходового ефекту.
У OpenGL, одному з найпопулярніших програмних інтерфейсів (API) для розробки додатків в області двовимірної і тривимірної графіки, зумовлюється видалення невидимих ліній і поверхонь здійснювати з використанням Z-буфера.
Застосування конкретного алгоритму для видалення невидимих частин зображення визначається багатьма чинниками, наприклад, типом зображуваних об'єктів, необхідним ступенем реалістичності, розташування джерела світла, виділеними обсягами пам'яті, обчислювальної складністю, простотою апаратної реалізації і т.д. У різних випадках ефективними можуть бути ті чи інші алгоритми. У зв'язку з цим у ряді програмних продуктів використовують кілька одночасно кілька алгоритмів видалення невидимих поверхонь.
Тільки якщо об'єкт сцени належить до певного класу, то можна вибрати найбільш підходящий алгоритм.