ІМІТІЦІЙНЕ МОДЕЛЮВАННЯ
В СИСТЕМІ SCILAB/XCOS

2. Теоретичні основи імітаційного моделювання

2.1. Концепція імітаційного моделювання

Імітаційне моделювання – це метод дослідження, який полягає у відтворенні властивостей реальних об'єктів за допомогою віртуальних об'єктів. Всі розрахунки в комп'ютерній моделі виконуються в так званому системному часі, який відповідає реальному часу функціонування об'єкта дослідження або системи у певному масштабі. Отже, імітаційним моделюванням називають відтворення на комп'ютері розгорнутого в часі процесу функціонування системи з урахуванням її взаємодії із зовнішнім середовищем.

Імітаційне моделювання – найбільш універсальний метод дослідження і оцінки ефективності систем, поведінка яких залежить від випадкових факторів. Моделі є хорошим засобом прогнозування поведінки об'єктів і систем. Моделювання дозволяє проводити контрольовані експерименти в ситуаціях, коли проведення експериментів на реальних об'єктах є недоцільним, небезпечним, неможливим або досить дорогим.

До імітаційного моделювання вдаються, коли:

• дорого або неможливо експериментувати на реальному об'єкті;
• неможливо побудувати аналітичну модель, тому що в системі є логічні причинно-наслідкові зв'язки, нелінійні динамічні блоки, стохастичні (випадкові) впливи;
• необхідно дослідити поведінку системи впродовж часу.

Основна задача імітаційного моделювання полягає у декомпозиції системи на відносно прості блоки (підсистеми), аналітичні моделі яких відомі або можуть бути легко отримані; поданні вхідних впливів на систему у вигляді послідовності числових значень, які надходять з певним інтервалом (інтервалом дискретизації процесів у часі); здійсненні їх перетворень послідовно та відповідно до математичних залежностей, які описують послідовність і зміст перетворення сигналів і даних у реальній системі.

Імітаційне моделювання суттєво спрощує процес отримання результатів через можливість використання агрегатного принципу. Це означає, що відпадає необхідність розв’язування складних систем рівнянь, які описують функціонування замкнених систем управління.

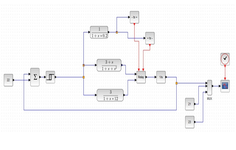
Пояснимо ці переваги на прикладі. Нехай необхідно здійснити моделювання нелінійної динамічної системи, структурна схема якої зображена на рис.1.5.

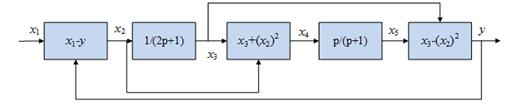
Наведена система описується системою рівнянь

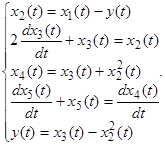
Отримати модель системи в цілому або розв’язати систему рівнянь важко, а інколи неможливо, через її нелінійність, а завдяки агрегатному принципу і імітаційному моделюванню результати можна отримати досить просто.

Найбільш розповсюдженим способом дослідження імітаційної моделі є статистичне моделювання.

Методика статистичного моделювання містить в собі ряд послідовних етапів:

• моделювання на комп’ютері випадкових впливів на систему у вигляді числових послідовностей із заданою кореляцією і законом розподілення ймовірностей;
• моделювання перетворення сигналів;
• статистична обробка результатів моделювання.

2.2. Генерування вхідних впливів

У системі Xcos передбачене генерування випадкових некорельованих впливів, розподілених за рівномірним або нормальним законом розподілу (рівномірний або нормальний білий шум). Генерування впливів з іншими розподілами ймовірностей є доволі складною задачею.

Задача дещо спрощується при генеруванні нормальної послідовності із заданою кореляційною функцією, оскільки отримання заданої кореляційної функції виконується шляхом лінійної фільтрації, яка не призводить до втрати нормальності розподілу послідовності даних.

Методика генерування нормальної послідовності із заданою кореляційною функцією передбачає використання початкової послідовності типу “нормальний білий шум» – таку послідовність звичайно генерують стандартні генератори. Спектральна щільність потужності такої послідовності є константою 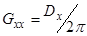. Методика складається з кроків:

1. Підготовчий етап:

1.1. Знаходження спектральної щільності необхідної послідовності як перетворення Фур’є заданої кореляційної функції ;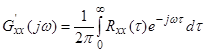

1.2. Знаходження амплітудно-частотної характеристики необхідного фільтра ;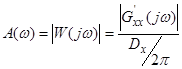

1.3. Знаходження відповідного дискретного перетворення за формулою (5.41);

2. Власне моделювання:

2.1. Генерування початкової послідовності типу нормального білого шуму з заданою дисперсією;

2.2. Перетворення її за знайденою формулою дискретної фільтрації – отримання вхідної послідовності для імітаційної моделі;

2.3. Імітація перетворення вхідних даних системою;

3. Обробка результатів імітаційного моделювання.

Окремим випадком є генерування числової послідовності з нормальним розподілом ймовірностей і експоненціальною автокореляційною функцією. Цей вид випадкової послідовності є найпоширенішим і найлегшим для генерування. Генерування здійснюється у два етапи:

1. Генерування некорельованої рівномірно розподіленої послідовності  {x_i} за допомогою будь-якої програми-генератора, які наразі є в усіх мовах програмування;

2. Перетворення на задану послідовність {x^'_j} методом підрахунку ковзного середнього

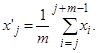
При m ≥ 6 через дію умов центральної граничної теореми теорії ймовірностей розподіл послідовності {x^'_j} буде близьким до нормального. Крім того, елементи цієї послідовності при утворенні мають різну кількість спільних доданків, наприклад:

при m = 6 маємо 

x^'₁ = x₁ + x₂ + ... x₆ ,

x^'₂ = x₂ + ... + x₆ + x₇ ,

x^'₃ = x₃ + ... + x₆ + x₇ + x₈ ,

тобто x^'₁ має 5 спільних доданків з x^'₂, 4 спільних доданки з x^'₃ і т. д., що приводить до поступового зменшення зв’язку між елементами отриманої послідовності. Це приблизно відповідає експоненціальному характеру кореляційної функції. Очевидно, інтервал кореляції цієї послідовності буде m – 1.

2.3. Обробка результатів імітаційного моделювання

Обробка результатів імітаційного моделювання здійснюється за тими ж правилами і методиками, що й обробка результатів реальних натурних експериментів. Зокрема, якщо моделями вхідних сигналів є випадкові числові послідовності, то для обробки результатів використовуються методи дисперсійного, кореляційного і регресійного аналізу.

2.4. Оцінювання необхідного обсягу тестів та трудомісткості імітаційного моделювання

Основою для визначення необхідного обсягу тестових даних є оцінка похибки імітаційного моделювання. Залежно від вигляду статистичних характеристик вихідних сигналів імітаційної моделі, які необхідно оцінити у конкретній задачі, похибки оцінки обчислюються за формулами:

• при оцінюванні розподілу ймовірностей способом підраховування кількості даних, які потрапляють у кожен інтервал розбиття діапазону можливих значень (спосіб побудови гістограми) відносна похибка розраховується за формулою

  

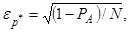
  де P_A – ймовірність потрапляння даного у окремий інтервал; N – обсяг вибірки.

  При оцінюванні розподілу ймовірностей на основі визначення відносного часу перебування у заданому інтервалі

  

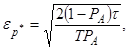
  де T – загальний час спостереження; τ – інтервал надходження дискретних даних;

• при оцінюванні середнього значення усієї множини результатів моделювання і відсутності кореляції між окремими результатами

  

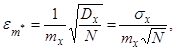
  де m_x і σ_x – математичне сподівання і с.к.в. результатів.

  При оцінюванні поточного середнього значення методом ковзного середнього на основі рекурентної формули 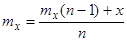і відсутності кореляції між окремими результатами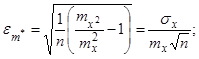

  

• при оцінюванні дисперсії нормально розподіленої послідовності і відсутності кореляції між окремими результатами

  ε_D =

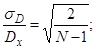
• при оцінюванні коефіцієнта кореляції на основі зіставлення часу перевищення деякого рівня U у двох корельованих послідовностях

  

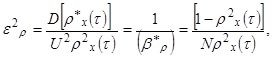
  де β*_ρ = U / σ*_ρ(τ).

З наведених співвідношень видно, що в усіх випадках похибка прямо чи опосередковано (через час проведення моделювання) залежить від кількості отриманих даних. Тому необхідна кількість даних може бути знайдена шляхом розв’язування нерівності

ε(N) ≤ ε_max

де ε_max – максимально допустима похибка моделювання.

Наприклад, для оцінювання закону розподілу ймовірностей шляхом побудови гістограми скористаємось нерівністю на основі формули

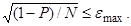
Якщо гістограма будується на 10 інтервалах розбиття діапазону можливих значень результатів і попередній гіпотезі, що цей закон близький до трикутного, розрахуємо мінімальну ймовірність (з формули видно, що кількість даних обернена до ймовірності)

,

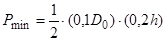де D₀ – діапазон; h – висота трикутного розподілу. Враховуючи, що 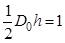, отримуємо P_min = 0,02.

Розв’язуючи нерівність відносно N, знаходимо, що для  отримання відносної статистичної похибки не гірше 0,1 (тобто 10% – досить неточний експеримент!) на кожному інтервалі необхідно мати N ≥ (1 – 0,02)/0,1², тобто не менше 98 даних, а усього для 10 інтервалів імітаційна вибірка повинна містити не менше 980 даних.

При попередній гіпотезі про нормальність закону розподілу результатів кількість даних повинна бути значно більшою, оскільки на кінцях діапазону значення ймовірності для нормального закону менше, ніж для трикутного. Очевидно, найменша кількість даних необхідна за умови гіпотези про рівномірний характер розподілу результатів.

Оскільки заздалегідь невідомо, виправдається висунута гіпотеза, чи ні, то найчастіше імітаційний експеримент проводять у два етапи: спочатку генерують мінімальну кількість даних, проводять експеримент, попередньо визначають тип розподілу ймовірностей результатів, а потім уточнюють розрахунок необхідної кількості даних і проводять додаткове моделювання.

2.5. Масштаби і масштабні співвідношення

В імітаційної моделі змінні відображаються відповідними «модельними змінними». Для переходу від вихідних математичних співвідношень до модельних змінних і для зворотного переходу кожної з змінних використовується відповідний масштаб.

Масштабом або масштабним коефіцієнтом математичної змінної x називається множник μ_x.

.

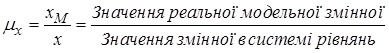Масштаб часу. Якщо позначити через τ час при імітаційному моделюванні, то зв'язок цього часу з часом уявлення реального процесу t виражається в такий спосіб:

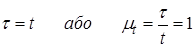 – натуральний масштаб часу;

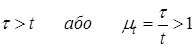 – сповільнений масштаб часу;

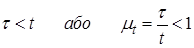 – прискорений масштаб часу.

З урахуванням масштабу імітаційні моделі отримуються з математичних співвідношень реальної моделі підстановкою

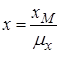
Наприклад, імітаційна модель закону всесвітнього тяжіння 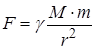отримується підстановкою:

F = F_M  ⁄ μ_F

γ = γ_M  ⁄ μ_γ

M = M_M  ⁄ μ_M

m = m_M  ⁄ μ_m

Тоді імітаційна модель матиме вигляд

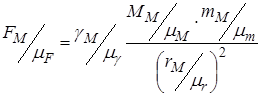
Звідки, виділивши окремо усі масштаби, отримуємо імітаційну модель

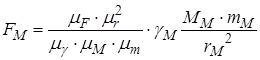
Перевагою використання масштабів є можливість приведення змінних до близьких діапазонів. Це дозволяє спостерігати процеси у одних осях. У розглянутому прикладі маси Землі Mі фізичного тіла m відрізняються на багато порядків, а використання різних масштабів дозволяє у імітаційній моделі зробити їх порівняними.