1.3.2 Особливості аналітичного статичного моделювання
Якщо за підсумками аналізу характеристик об'єкта моделювання він був віднесений до класу стаціонарних (вихід залежить тільки від входу, об'єкт не змінюється в часі), то можливе застосування даної методики, яка є окремим випадком загальної методики моделювання.
У випадку, коли на стадії аналізу вдалося встановити майже всі зв’язки між характеристиками об’єкту, це відображається в концептуальній моделі, по якій відбувається розробка формальних залежностей моделі. Зазвичай, статична модель подається у вигляді одного рівняння або системи рівнянь чи нерівностей, лінійних чи нелінійних, алгебраїчних чи трансцендентних. Якщо інформації про залежність характеристик недостатньо для їх точної ідентифікації, або зв’язки мають випадковий характер, об’єкт моделювання розглядається як «чорна скриня», стосовно якого виділяються лише входи та виходи, а внутрішні зв’язки вважаються невідомими. Для ідентифікації моделі в цьому випадку може бути застосований апарат регресійного аналізу. Розглянемо ситуацію, коли у об’єкта одна вихідна величина та декілька вхідних величин. Такі об’єкти в концептуальній моделі представляються у вигляді зображеному на рис 1.2, на якому 
,..,
– вхідні змінні (фактори, регресори), 
– вихідна змінна (відгук).
Рисунок 1.2. – Об’єкт моделювання «чорна скриня»
При цьому приймаються припущення, які визначають стаціонарність об’єкту, відсутність взаємозв’язку між різними реалізаціями процесу. Наприклад, у якості відгуку можна розглянути витрати палива автомобілем на 100 км шляху. Факторами будуть вага вантажу, середня швидкість руху. Припущення: рух відбувається в основному по горизонталі по однотипних дорогах; якість палива, технічний стан автомобіля та водій не змінюються.
Структура математичної моделі може бути лінійною чи нелінійною. Розглянемо найпростіший випадок, коли залежність вихідної змінної від факторів має вигляд:
, (1.1)
де 
, ..., 
– невідомі параметри.
Для пошуку значень параметрів полінома (1.1) може бути застосований один з методів параметричної ідентифікації, наприклад, метод найменших квадратів (МНК, least squares method), який докладніше викладений у розділі 6.
Методика застосування МНК складається з етапів:
Збір статистичних даних здійснюється в ході експерименту. Результати експерименту представляються у вигляді таблиці 1.2.
Таблиця 1.2
Результати експерименту
№ |
|
|
… |
|
1 |
|
|
… |
|
… |
… |
… |
… |
… |
m |
|
|
… |
|
Рядки в таблиці відповідають результатам окремого експерименту. Кількість записів у таблиці має дорівнювати або бути більше числа факторів. Чим більше експериментальних даних, тим більше інформації для побудови моделі. Однак слід пам’ятати, що кожний експеримент має певну вартість.
З метою дослідження об’єкту дані експерименту піддаються статистичній обробці і аналізу. На основі даних:
Дослідження статистичної інформації дає змогу частково виявляти помилки вводу та методики проведення експерименту. Аналіз кореляційної матриці дозволяє з’ясувати ступінь взаємозв’язку відгуку з факторами, та факторів між собою.
Для проведення розрахунків результати експерименту представляються у вигляді матриць:
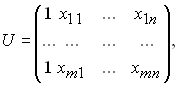
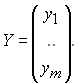
Розрахунок значень стовпця параметрів В поліному (1.1) відбувається за формулою МНК:
.
Отриманий поліном визначає середньостатистичне значення відгуку при заданих значеннях факторів. Це означає, що для адекватної моделі значення її вихідної змінної може значно відрізнятися від значення вихідної величини об’єкту, але на великій кількості спостережень при однакових значеннях факторів середнє експериментальне значення відгуку буде близьким до розрахованого по моделі.
Для оцінки якості побудованої моделі використовують різні статистичні оцінки (наприклад, залишкова дисперсія, критерій Фішера та інші). З метою поліпшення цих оцінок можливо застосовувати наступні прийоми:
Для видалення з моделі малозначущих змінних застосовують процедуру багатокрокового регресійного аналізу. Його суть полягає в тому, що після знаходження для полінома (1.1) значень параметрів та оцінок якості, для кожного фактора розраховують статистичну значимість стосовно впливу на відгук. Зі структури моделі та з інформаційної таблиці видаляється фактор з найменшою значимістю і його експериментальні дані. Після цього процедура розрахунку значень параметрів і оцінок якості моделі повторюється. Якщо без цього фактору оцінки моделі покращилися, то його видалення вважається успішним і переходять до наступного фактору з найменшою значимістю. Інакше процедура припиняється і оптимальним по структурі є останній успішно знайдений поліном.
Поліпшення оцінок полінома також можна досягти шляхом видалення частини рядків з інформаційної матриці. Видаляються рядки, при підстановці з яких значень факторів відповідне значення відгуку моделі дуже сильно, порівняно з іншими рядками, відрізняється від фактичного значення вихідної величини об'єкту (так звані ізольовані точки). Обгрунтованість видалення полягає в тому, що, можливо, ці дані не є типовими для функціонування об’єкту. При кожному видаленні необхідно приймати рішення, наскільки дані в рядку типові для об'єкту, і контролювати зміну значень оцінок моделі. Видалити можна лише невелику частину даних, щоб не погіршити їх статистичну достовірність в цілому.
Якщо лінійна структура моделі не дозволяє досягти необхідного рівня значень оцінок критеріїв якості, до неї можна додавати нелінійні компоненти (наприклад, добуток факторів чи їх ступені). Для застосування МНК нелінійні складові перетворюють у лінійні шляхом спеціальних замін, перераховують інформаційну матрицю, а після розрахунку значень параметрів лініаризованої моделі зворотною процедурою визначають параметри нелінійної моделі. Наприклад, поліном 
може бути легко перетворений на лінійний 
шляхом заміни 
, при чому параметри поліному залишаються ті самі.
Для розробленої моделі завжди виконується перевірка адекватності на основі нової серії експериментів.
Як видно з зазначеного вище, розробка аналітичних моделей є клопіткою та витратною справою. Крім того, однією з проблем аналітичного моделювання є врахування істотних випадкових впливів на об’єкт. З цією задачею легше впоратися, використовуючи арсенал імітаційного моделювання, який спирається на засоби ЕОМ.
