1.4.3 Особливості імітаційного статистичного моделювання
Аналітичне імовірнісне моделювання полягає в побудові моделей, які оперують не з конкретними випадковими числовими послідовностями, а безпосередньо з їх імовірнісними (закони розподілу ймовірності) і спектральними (спектральні щільності або кореляційні функції) характеристиками. У загальному випадку побудова аналітичних імовірнісних моделей є надто складною обчислювальною задачею, що не дозволяє повною мірою використовувати такі їх переваги, як можливість точного аналітичного завдання характеристик випадкових процесів, відсутність необхідності генерації і обробки великих вибірок випадкових чисел, пристосованість до оперативної оптимізації. У літературі описані результати досліджень, направлених на створення спеціалізованих проблемно-орієнтованих систем і пакетів прикладних програм, що об'єднують чисельні алгоритми розв’язання найбільш характерних обчислювальних процедур аналітичного імовірнісного моделювання і способи описання структур систем. Ці засоби мають, як правило, вузькоспеціалізовану спрямованість на моделювання певних класів складних систем.
З цих причин основним методом стохастичного комп’ютерного моделювання залишається метод статистичного імітаційного моделювання.
Методика статистичного моделювання включає ряд послідовних етапів: моделювання псевдовипадкових числових послідовностей із заданою кореляцією і законом розподілу ймовірностей, що імітують вхідні сигнали і збурення в системі; моделювання перетворення отриманих числових послідовностей в системі; статистична обробка результатів моделювання. Розглянемо перераховані етапи.
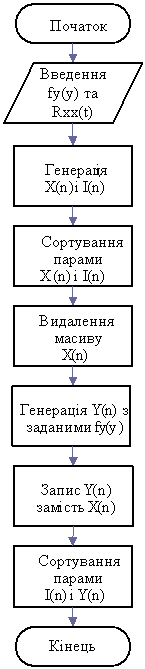
Комп’ютерне моделювання псевдовипадкових числових послідовностей із заданими характеристиками. При побудові імітаційної моделі системи виникає завдання отримання псевдовипадкових числових послідовностей із заданою кореляцією і законом розподілу ймовірностей. Відомим є метод отримання числових послідовностей із заданими статистичними характеристиками за допомогою сортування вихідних послідовностей. Метод заснований на тому, що коефіцієнт кореляції випадкових чисел більше залежить від порядку їх розташування в числовому ряді, ніж від величини. Тому дві псевдовипадкові послідовності, які відповідають двом різним розподілам, у випадку, коли вони однаково упорядковані, матимуть приблизно рівні коефіцієнти кореляції.
У випадку з методом сортування, генерується псевдовипадкова послідовність ![]() із заданою кореляційною функцією, але довільним розподілом. У відповідність їй ставиться послідовність цілих чисел
із заданою кореляційною функцією, але довільним розподілом. У відповідність їй ставиться послідовність цілих чисел ![]() . Потім обидві послідовності попарно сортуються. При цьому величини
. Потім обидві послідовності попарно сортуються. При цьому величини ![]() розміщуються за зростанням, а масив
розміщуються за зростанням, а масив ![]() запам'ятовує їх попереднє положення (місця в неупорядкованому масиві
запам'ятовує їх попереднє положення (місця в неупорядкованому масиві ![]() ). Таким чином, цілочисловий масив
). Таким чином, цілочисловий масив ![]() відображає кореляцію між елементами масиву
відображає кореляцію між елементами масиву ![]() . Після упорядкування масив
. Після упорядкування масив ![]() не представляє інтересу, оскільки вся інформація про кореляційну функцію тепер міститься в масиві
не представляє інтересу, оскільки вся інформація про кореляційну функцію тепер міститься в масиві ![]() . Потім генерується псевдовипадкова послідовність
. Потім генерується псевдовипадкова послідовність ![]() із заданим розподілом і нульовою кореляцією і записується на місце масиву
із заданим розподілом і нульовою кореляцією і записується на місце масиву ![]() . Після цього вона сортується у порядку зростання. Далі масиви
. Після цього вона сортується у порядку зростання. Далі масиви ![]() і
і ![]() попарно сортуються, причому масив
попарно сортуються, причому масив ![]() розташовується у зростаючому порядку. Структурна схема алгоритму наведена на рис. 1.7 а.
розташовується у зростаючому порядку. Структурна схема алгоритму наведена на рис. 1.7 а.
У результаті виконання даного алгоритму отримаємо псевдовипадкову числову послідовність, яка містить величини, що розподілені за заданим законом і мають задану кореляційну функцію. Алгоритм сортування доцільно використовувати у випадках, коли для статистичного моделювання системи є невеликий об'єм статистичних даних, що не вимагають операції над числовими масивами великої розмірності. При великій розмірності масивів істотно збільшується час моделювання.
Відомим є алгоритм фільтрації, що вимагає менших витрат машинного часу для здобуття випадкового процесу із заданою кореляцією і законом розподілу ймовірностей. В якості вихідного вибирається нормальний стаціонарний випадковий процес ![]() . Завжди існує таке нелінійне неінерційне перетворення
. Завжди існує таке нелінійне неінерційне перетворення ![]() , яке перетворює нормальну функцію щільності
, яке перетворює нормальну функцію щільності ![]() процесу
процесу ![]() в задану функцію щільності
в задану функцію щільності ![]() . Якщо вихідний процес
. Якщо вихідний процес ![]() має кореляційну функцію
має кореляційну функцію ![]() , то перетворений процес
, то перетворений процес ![]() матиме кореляційну функцію
матиме кореляційну функцію ![]() , що відрізняється від функції
, що відрізняється від функції ![]() і пов'язаний з нею деякою залежністю
і пов'язаний з нею деякою залежністю ![]() . Вигляд цієї залежності визначається перетворенням
. Вигляд цієї залежності визначається перетворенням ![]() . Для того, щоб кореляційна функція перетвореного процесу була потрібною, необхідно вибрати кореляційну функцію вихідного процесу:
. Для того, щоб кореляційна функція перетвореного процесу була потрібною, необхідно вибрати кореляційну функцію вихідного процесу:
![]()
де ![]() – функція, обернена до
– функція, обернена до ![]() .
.
При використанні даного способу, підготовча робота складається з декількох етапів:
Після закінчення підготовчої роботи, моделювання випадкового процесу із заданими характеристиками зводиться до формування дискретних реалізацій ![]() нормального випадкового процесу
нормального випадкового процесу ![]() і до перетворення цих реалізацій за формулою
і до перетворення цих реалізацій за формулою
![]()
Структурна схема описаного алгоритму наведена на рис. 1.6 б.
|
|
а) б)
Рисунок 1.6 – Структурні схеми алгоритмів
Описаний алгоритм вимагає менших витрат машинного часу, ніж алгоритм сортування, не вимагає накопичення і зберігання в пам'яті числових масивів великої розмірності. Недоліками методу є його складність для програмування і великий обсяг підготовчої роботи. Ускладнення принципового характеру полягає в тому, що в загальному випадку не представляється можливим довести існування розв’язку рівняння ![]() відносно
відносно ![]() .
.
При використанні обох описаних алгоритмів виникає задача генерування на комп’ютері псевдовипадкових числових послідовностей із заданими законами розподілу і нульовою кореляцією, та псевдовипадкових числових послідовностей із заданою кореляційною функцією і довільним розподілом. Задачу генерування випадкових чисел із заданим законом розподілу вирішують у декілька етапів. Спочатку отримують послідовність рівномірно розподілених на інтервалі [0, 1] псевдовипадкових чисел, а з неї – послідовність псевдовипадкових чисел із заданим законом розподілу.
Розглянемо алгоритмічні (програмні) методи отримання рівномірно розподілених випадкових чисел (на практиці інколи застосовують також фізичне моделювання з використанням спеціальної комп’ютерної приставки). Суть програмних методів полягає в тому, що рівномірно розподілені псевдовипадкові числа обчислюють за допомогою деякої рекурентної формули, де кожне наступне ![]() -ше значення утворюється з попереднього i (або групи попередніх) шляхом застосування деякого алгоритму, що містить логічні і арифметичні операції.
-ше значення утворюється з попереднього i (або групи попередніх) шляхом застосування деякого алгоритму, що містить логічні і арифметичні операції.
Існує велика кількість способів імітації рівномірного розподілу (методи формування залишків, поетапного підсумовування, зрізання, перемішування). Загальними для всіх цих методів є вимоги, що застосовуються до послідовності, що генерується, рівномірно розподілених випадкових чисел: кількість операцій для отримання кожного псевдовипадкового числа має бути мінімальною; випадкові числа генеруються як можна менш корельованими, а їх розподіл – близьким до рівномірного, причому вигляд розподілу і ступінь корельованості чисел не повинні змінюватися у процесі роботи програми.
У стандартному математичному і програмному забезпеченні різних типів комп’ютерів є спеціальні процедури і підпрограми для генерації рівномірно розподілених послідовностей псевдовипадкових чисел.
Використовуючи рівномірно розподілену на інтервалі [0,1] випадкову величину X, можна отримати послідовність випадкових чисел з довільним заданим законом розподілу ймовірностей. Розрізняють три основні способи формування таких послідовностей:
1) пряме перетворення числа ![]() , що є реалізацією випадкової величини
, що є реалізацією випадкової величини ![]() , рівномірно розподіленої на інтервалі [0, 1] за допомогою деякої функції
, рівномірно розподіленої на інтервалі [0, 1] за допомогою деякої функції ![]() , в число
, в число ![]() , яке може розглядатися як реалізація випадкової величини Y, що має заданий закон розподілу;
, яке може розглядатися як реалізація випадкової величини Y, що має заданий закон розподілу;
2) відсіювання чисел з первинної послідовності рівномірно розподілених на інтервалі [0, 1] псевдовипадкових чисел так, щоб числа, що залишилися, були розподілені за заданим законом;
3) моделювання умов відповідних граничних теорем теорії ймовірностей.
Широкого поширення набувають способи прискореної генерації випадкових чисел. Так, значний ефект збільшення швидкодії при імітації випадкових чисел, розподілених за нормальним законом, у порівнянні зі способом, заснованим на використанні центральної граничної теореми теорії ймовірностей, дає спосіб, що включає запропонований Мюллером алгоритм, за яким пара незалежних рівномірно розподілених на відрізку [0,1] чисел ![]() перетворюється в пару незалежних нормально розподілених величин
перетворюється в пару незалежних нормально розподілених величин
![]()
Відзначимо, що цей спосіб є теоретично точним і вимагає найменшої кількості рівномірно розподілених чисел ![]() .
.
Відомі спеціальні способи здобуття випадкових чисел, що підкоряються ряду законів розподілу вірогідності. Наприклад, розподіл Релея визначається одним параметром, рівним середньому квадратичному відхиленню вихідного двовимірного нормального розподілу. Звідси витікає наступний спосіб імітації розподілу Релея:
![]()
де ![]() – випадкове число, розподілене за законом Релея, а
– випадкове число, розподілене за законом Релея, а ![]() та
та ![]() – випадкові числа, що мають нормальний розподіл з нульовим математичним сподіванням і рівним одиниці середнім квадратичним відхиленням.
– випадкові числа, що мають нормальний розподіл з нульовим математичним сподіванням і рівним одиниці середнім квадратичним відхиленням.
Існує також співвідношення, що пов'язує випадкові числа, розподілені згідно із законом Релея, з випадковими числами ![]() , рівномірно розподіленими на відрізку [0, 1], яке визначає інший спосіб генерації:
, рівномірно розподіленими на відрізку [0, 1], яке визначає інший спосіб генерації:
![]()
Для імітації закону розподілу Максвелла можна скористатися тим, що випадкова величина, яка підлягає розподілу Максвелла, може розглядатися як модуль тривимірного випадкового вектора, проекції якого на осі координат підлягають нормальному розподілу з рівними між собою середнім квадратичним відхиленням і математичними сподіваннями, що дорівнюють нулю. Тому можна скористатися наступною формулою для імітації закону розподілу Максвелла:
![]()
де ![]() – випадкове число, розподілене за законом Максвелла;
– випадкове число, розподілене за законом Максвелла; ![]() – випадкові числа, що мають нормальний розподіл з математичними сподіваннями, рівними нулю, і середніми квадратичними відхиленнями, рівними одиниці.
– випадкові числа, що мають нормальний розподіл з математичними сподіваннями, рівними нулю, і середніми квадратичними відхиленнями, рівними одиниці.
Розглянемо способи здобуття псевдовипадкових числових послідовностей із заданою кореляційною функцією. Відомий алгоритм, де n некорельованих випадкових чисел ![]() піддають такому лінійному перетворенню, після якого отримані величини
піддають такому лінійному перетворенню, після якого отримані величини ![]() мають задану кореляційну матрицю
мають задану кореляційну матрицю ![]() .
.
Таким чином, величини знаходяться з матричного рівняння
![]()
де ![]() – лінійне перетворення вектора-стовпця
– лінійне перетворення вектора-стовпця ![]() в
в ![]() .
.
У розгорнутому вигляді отримуємо:
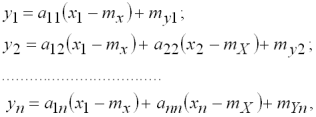
де коефіцієнти перетворення ![]() визначаються з рівняння вигляду
визначаються з рівняння вигляду
![]()
а ![]() – вектор-стовпець математичних сподівань
– вектор-стовпець математичних сподівань![]() .
.
При великих значеннях n викладений спосіб генерування корельованих псевдовипадкових послідовностей стає незручним для реалізації на ЕОМ, оскільки запам'ятовування елементів матриці ![]() вимагає великого об'єму оперативної пам'яті
вимагає великого об'єму оперативної пам'яті ![]() комірок) і великого обсягу обчислень (витрат машинного часу). У зв'язку з цим, у ряді випадків виявляється зручнішим моделювання корельованих випадкових процесів за методом канонічних розкладань. Нехай безперервний випадковий процес
комірок) і великого обсягу обчислень (витрат машинного часу). У зв'язку з цим, у ряді випадків виявляється зручнішим моделювання корельованих випадкових процесів за методом канонічних розкладань. Нехай безперервний випадковий процес ![]() заданий канонічним розкладанням
заданий канонічним розкладанням
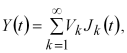 (1.2)
(1.2)
де ![]() – некорельовані випадкові коефіцієнти;
– некорельовані випадкові коефіцієнти; ![]() – система деяких детермінованих координатних функцій.
– система деяких детермінованих координатних функцій.
Цифрове моделювання (digital simulation) випадкового процесу, заданого канонічним розкладанням, здійснюється таким чином. У якості ![]() використовуються значення некорельованих випадкових величин
використовуються значення некорельованих випадкових величин ![]() , а безкінечний ряд (1.2) при обчисленнях приблизно замінюється зрізаним кінцевим рядом. Використовуючи канонічне розкладання, отримаємо співвідношення для моделювання
, а безкінечний ряд (1.2) при обчисленнях приблизно замінюється зрізаним кінцевим рядом. Використовуючи канонічне розкладання, отримаємо співвідношення для моделювання
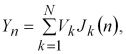
у якому дисперсії ![]() некорельованих випадкових величин
некорельованих випадкових величин ![]() і дискретні координатні функції
і дискретні координатні функції ![]() знаходяться з наступних рекурентних співвідношень:
знаходяться з наступних рекурентних співвідношень:
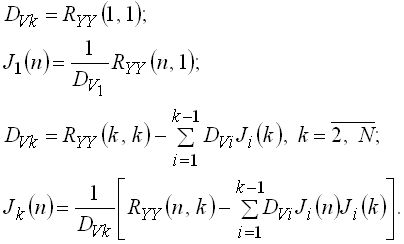
Звідси отримуємо
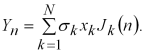
Послідовність ![]() матиме нормальний розподіл і задану кореляційну функцію
матиме нормальний розподіл і задану кореляційну функцію ![]() .
.
Методи сортування і фільтрації у поєднанні з розглянутими способами генерування псевдовипадкових числових послідовностей із заданими кореляційними функціями дозволяють отримати послідовності випадкових чисел, що імітують вхідні сигнали і збурені дії в об'єкті моделювання.
Моделювання процесів перетворення випадкових сигналів. Розглянемо способи побудови алгоритмів для моделювання процесів перетворення випадкових сигналів різними перетворювачами і системами. При моделюванні перетворення випадкових сигналів лінійними динамічними системами зручно користуватися їх імпульсною характеристикою ![]() .
.
Для отримання цифрової моделі перетворення вхідного випадкового сигналу необхідно моделювати операцію згортки функцій ![]() та
та ![]() .
.
Здійснюючи заміну інтеграла Дюамеля сумою дискретних значень за методом прямокутників, отримуємо
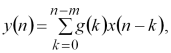 (1.3)
(1.3)
де ![]() – дискретний аналог тривалості перехідного процесу.
– дискретний аналог тривалості перехідного процесу.
Існують також точніші методи інтегрування – квадратурні формули Ньютона-Котеса (трапецій, Сімпсона тощо). У цих випадках формула (1.3) набирає вигляду
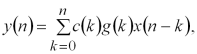
де коефіцієнти ![]() визначаються залежно від методу чисельної інтеграції, що був застосований.
визначаються залежно від методу чисельної інтеграції, що був застосований.
Істотною перевагою методу моделювання лінійних динамічних систем на основі дискретного аналога інтеграла згортки є можливість узагальнення його на випадок моделювання лінійних динамічних систем зі змінними параметрами (нестаціонарних систем).
Нестаціонарна система (non-stationary system) описується імпульсною характеристикою ![]() , залежною від двох змінних. У цьому випадку реакцію нестаціонарної системи на випадковий сигнал запишемо у вигляді
, залежною від двох змінних. У цьому випадку реакцію нестаціонарної системи на випадковий сигнал запишемо у вигляді
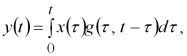
або в дискретній формі

Описаний метод застосовується у тих випадках, коли моделювання вхідного випадкового сигналу здійснюється за допомогою алгоритмів нелінійного перетворення, фільтрації і моделювання умов граничних теорем теорії вірогідності. Структурна схема алгоритму моделювання представлена на рис. 1.7.
Відзначимо, що у разі моделювання вхідного випадкового сигналу (random signal) на основі алгоритму сортування (див. рис. 1.6 а) побудувати імітаційну модель системи неможливо і досліджувати її доцільно матричними методами. Цифрові моделі замкнутих нелінійних систем, що є комбінованими комбінаціями лінійних динамічних і нелінійних статичних перетворювачів, можна побудувати на основі алгоритмів, моделюючих перетворення сигналів в окремих перетворювачах (рис. 1.8).
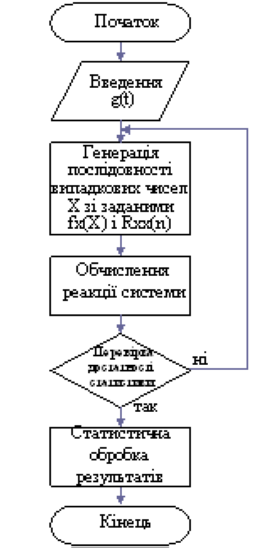
Рисунок 1.7 – Структурна схема алгоритму моделювання нестаціонарної системи
Моделювання описаних систем часто пов'язане із значними труднощами, проте у ряді випадків структурну схему системи можна представити у спрощеному вигляді (рис. 1.9).
У цьому випадку
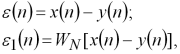 (1.4)
(1.4)
де ![]() – оператор нелінійного перетворювача системи.
– оператор нелінійного перетворювача системи.
Застосовуючи далі описаний вище алгоритм для цифрового моделювання лінійних динамічних систем, отримуємо
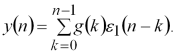
Таким чином, особливістю цифрових моделей нелінійних замкнених систем є необхідність вирішення на кожному кроці нелінійних алгебраїчних рівнянь вигляду (1.4) за умови, що лінійні динамічні ланки системи моделюються на основі дискретної згортки.
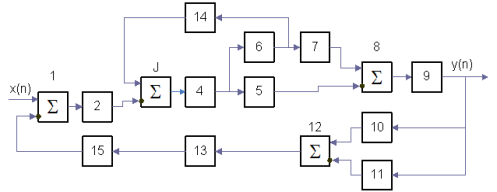
Рисунок 1.8 – Цифрова модель замкнутої нелінійної системи
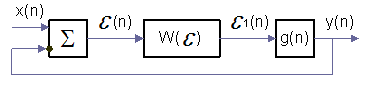
Рисунок 1.9 – Спрощений вигляд структурної схеми
Рішення цієї задачі можна спростити, якщо в ланцюг зворотного зв'язку системи ввести елемент затримки на один період. Тоді нелінійне рівняння (1.4) перетвориться в рекурентне:
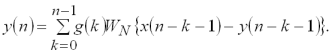
Введення в ланцюг зворотного зв'язку елемента затримки, вносить додаткову похибку до цифрової моделі. Проте, на кроці дискретизації еквівалентна дискретна система з елементом затримки так само, як і без нього, збігається з вихідною безперервною системою. Тому, вибором кроку дискретизації можна досягти як завгодно малого впливу похибки затримки.
Завершальним етапом статистичного моделювання є статистична обробка результатів.
Кількість реалізацій і точність обчислень. Кількість реалізацій при вирішенні завдань методом статистичного моделювання визначається необхідною точністю отримуваних результатів.
Нехай метою моделювання буде обчислення ймовірності Р появи деякої випадкової події A (наприклад, при дослідженні точності контролю розмірів виробів, ймовірності приналежності розмірів виробу до певної сортувальної групи; ймовірності того, що виріб буде застрахований при вторинному контролі, якщо при первинному контролі його визнано придатним). В якості оцінки для шуканої ймовірності Р застосовується частота L/N настання події А при N реалізаціях, де L – кількість випробувань, при яких відбувається подія А. Враховуючи центральну граничну теорему теорії ймовірностей, частота L/N при чималих N має нормальний розподіл, який визначається математичним сподіванням M(L/N)= Р і дисперсією D(L/N)= Р (1-P) / N.
Отже

При чималих N отримуємо
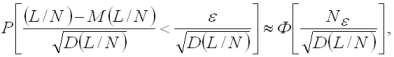 (1.5)
(1.5)
де 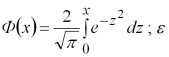 – точність нерівності.
– точність нерівності.
Враховуючи певну ймовірність Р, знайдемо по таблицях нормального розподілу значення D(L/N), що задовольняє рівнянню ![]() , де
, де ![]() .
.
Надійну оцінку L/N отримуємо у вигляді
![]() , (1.6)
, (1.6)
Згідно формулі (1.6) з ймовірністю більше ніж 0,997, величина L/N задовольняє умові
![]()
Таким чином, похибка методу статистичного моделювання при обчисленні ймовірності події А ніколи не перевищує величини ![]() і спадає зі збільшенням числа випробувань обернено пропорційно кореню квадратному з N. Звідси можна визначити кількість реалізацій N, необхідних для отримання оцінки L/N з точністю
і спадає зі збільшенням числа випробувань обернено пропорційно кореню квадратному з N. Звідси можна визначити кількість реалізацій N, необхідних для отримання оцінки L/N з точністю ![]() і достовірністю Р
і достовірністю Р
![]()
або для Р =0,997
![]()
Аналогічно можна оцінити кількість реалізацій, необхідних для оцінки за результатами моделювання середнього значення випадкової величини. Припустимо, що здійснюється формування N реалізацій випадкової величини X, що має середнє значення М і дисперсію ![]() . Визначимо
. Визначимо

В силу центральної граничної теореми теорії ймовірностей
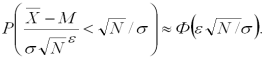
Тоді
![]()
а точність
![]() (1.7)
(1.7)
Розв’язуючи (1.7) відносно N, отримаємо
![]() . (1.8)
. (1.8)
При Р=0,997 формули (1.7) і (1.8) відповідно, набувають вигляду:
![]()
Похибка методу статистичного моделювання як при обчисленні ймовірності події А, так і при оцінці середнього значення випадкової величини складає ![]() . Зменшення похибки
. Зменшення похибки ![]() наближеного розв’язку задачі методом імовірнісного моделювання пов'язане зі значним збільшенням числа випробувань N, а відповідно, і зі збільшенням часу обчислень. Наприклад, збільшення точності на порядок призводить до подовження часу розв’язку задачі у сто разів.
наближеного розв’язку задачі методом імовірнісного моделювання пов'язане зі значним збільшенням числа випробувань N, а відповідно, і зі збільшенням часу обчислень. Наприклад, збільшення точності на порядок призводить до подовження часу розв’язку задачі у сто разів.