1.5 Похибки та властивості обчислювальних алгоритмів

 

Сьогодні множина методів, які використовуються для комп’ютерних обчислень, ширша, ніж множина саме обчислювальних методів чи так званих методів наближених обчислень. Але на практиці все ж таки саме ці методи стають основою для побудови комп’ютерних розв’язків математичних моделей систем та процесів. В них розглядаються такі алгоритми, які найчастіше пов’язані з розв’язанням дискретної задачі, що була задана як дискретна, чи виникла як результат дискретизації вихідної неперервної задачі. Простішим прикладом дискретизації може слугувати побудова різницевої схеми, що виникає при заміні диференціальних рівнянь кінцево-різницевими співвідношеннями. При дискретизації неперервної задачі обов’язково виникає похибка дискретизації (sampling error). Ця похибка є однією з головних складових в похибці обчислювального методу.

Іншою складовою методичної похибки є похибка округлення (rounding error), яка виникає завдяки скінченній довжині розрядної сітки комп’ютера, що призводить до наближеного представлення дійсних чисел. Величина цієї похибки визначається не тільки довжиною розрядної комп’ютерної сітки, а також чутливістю конкретного алгоритму до похибок округлення.

Можна виділити також похибку зрізання (truncation error), що виникає при заміні нескінченних рядів скінченними.

Похибки можна класифікувати за способом представлення як абсолютні та відносні.

Абсолютна похибка (absolute error)визначається як модуль різниці між точним А та наближеним а значеннями числа:

.

Відносна похибка (relative error) визначається, як:

.

Без доведення (доведення дуже просте і для тренування його можна зробити самостійно) наведемо головні властивості арифметичних операцій з похибками:

– абсолютна похибка суми к (к – будь-яке ціле число) наближених чисел не перебільшує суми абсолютних похибок цих чисел

;

– відносна похибка суми к наближених чисел не перебільшує максимальної відносної похибки одного з цих чисел

_;

– відносна похибка добутку к наближених чисел не перебільшує суми відносних похибок цих чисел

,

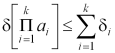де _.

Використовується також відносна похибка, де в знаменнику замість використовується діапазон а від максимального до мінімального значення. Тому похибку називають зведеною

.

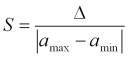Треба розділяти локальні та глобальні похибки (local and global errors). Локальні виникають на кожному конкретному кроці обчислювального алгоритму, а глобальні включають всі похибки, що виникли як на цьому кроці обчислень, так і на попередніх (ці похибки називають похибками наслідування чи похибками поширення).

При оцінці глобальних похибок часто використовуються поняття максимальної похибки

,

середньої похибки

,

середньої квадратичної похибки

.

Одним із головних критеріїв якості обчислювальних алгоритмів (окрім похибки, при застосуванні наближених методів) є їх швидкодія, тобто кількість елементарних обчислювальних операцій (додавання, зсув, інверсія), яка потрібна для реалізації алгоритму.

Важливим є поняття ітераційного алгоритму (iterative algorithm), що визначається як багатокроковий алгоритм, в якому кожний наступний крок виконується на основі попереднього. Причому можна відокремити суто ітераційні алгоритми за допомогою ітераційних процедур, де розглядаються розв’язки в окремих точках, та багатокрокові алгоритми, в яких розв’язок в попередній точці є основою для пошуку наступної. Збіжність є головною властивістю суто ітераційних алгоритмів: якщо вони незбіжні, то застосувати їх взагалі неможливо.

Наведемо декілька головних визначень щодо властивостей обчислювальних методів та алгоритмів.

Стійкість алгоритму (stability of the algorithm) – здатність виконувати обчислення і отримувати кінцевий результат із заданою точністю при зміні параметрів алгоритму і вхідних даних в деякій області, яка називається областю стійкості.

Збіжність (convergence) – це властивість алгоритму шляхом зміни його параметрів виконувати обчислення з скільки завгодно малою похибкою для заданого класу вхідних даних (тобто при збільшенні кількості ітерацій для алгоритмів, що збігаються, похибка буде прагнути до нуля).

Причому підвищення точності досягається зміною внутрішніх параметрів алгоритму (наприклад, максимально допустимою різницею між попереднім та наступним наближенням).

Коректність обчислювального методу (the correctness of computational method) – це властивість безперечного існування розв’язку задачі та забезпечення стійкості обчислювального алгоритму, що реалізує цей метод.