
Розділ 2 Задачі лінійної алгебри
В цьому розділі розглянуто розв’язання двох найбільш поширених обчислювальних задач лінійної математики: розв’язання систем лінійних рівнянь та відшукання власних значень та власних векторів матриць. Причому вважається, що користувач вже знайомий з головними відомостями з теорії матриць.
2.1 Розв’язання систем лінійних рівнянь
У загальному випадку задача формулюється таким чином: знайти значення ![]() , що задовольняють систему з
, що задовольняють систему з ![]() лінійних алгебраїчних рівнянь (СЛАР, system of linear algebraic equations):
лінійних алгебраїчних рівнянь (СЛАР, system of linear algebraic equations):
 (2.1)
(2.1)
або в матричній формі ![]() , де
, де
 ,
,
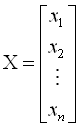 ,
,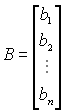 .
.
Геометричний сенс розв’язку СЛАР полягає в пошуку точки перетину n-мірних гіперплощин у n-мірному гіперпросторі. Розв’язком є стовпець Х. Якщо рівнянь лише два, то маємо випадок двох прямих на площині, які можуть перетинатися, бути паралельними або співпадати. Тому будь-яка СЛАР може мати:
1) єдиний розв’язок;
2) безкінечну множину розв’язків;
3) не мати розв’язку взагалі.
Необхідною і достатньою умовою існування єдиного розв’язку є нерівність нулю визначника ![]() (лінійна незалежність рівнянь):
(лінійна незалежність рівнянь):
![]() .
.
Методи розв’язання систем лінійних рівнянь можна розділити на прямі та ітераційні. До прямих, які дозволяють одержати точний розв’язок, відносяться методи визначників Крамера, Гаусса, прогонки. Ітераційні методи, що ґрунтуються на одержанні і уточненні послідовних наближень до точного розв’язку, ефективні в тому випадку, коли є багато нульових коефіцієнтів або високий порядок системи (метод Гаусса ефективний до порядку 104, ітераційні – до 106).