2.1.1 Прямі методи

 

До найбільш популярних прямих методів відносять метод Гаусса та його різновиди, метод Крамера (визначників), метод оберненої матриці, а також метод прогонки, що використовується в задачах з діагональними матрицями. Проте, метод Крамера (визначників), детально розглянутий в стандартних курсах вищої математики, не може бути застосований в більшості практичних задач через велику складність розрахунку визначників навіть при невеликому зростанні порядку системи. Тому в цьому розділі буде зосереджено увагу на розгляді методу Гаусса, який, якщо й поступається ітераційним методам в певних практичних областях, все ж таки є найбільш універсальним, а також методу прогонки, що використовується в задачах з діагональними матрицями.

 

2.1.1.1 Метод Гаусса

 

Цей метод є одним з найпоширеніших методів рішення СЛАР. У його основі лежить ідея послідовного виключення невідомих, що приводить вихідну систему до трикутного виду, у якому всі коефіцієнти нижче головної діагоналі дорівнюють нулю. Існують різні обчислювальні схеми, що реалізують цей метод. Найбільше поширення мають схеми з вибором головного елемента по рядку, по стовпцю, або по всій матриці.

Класичний метод Гаусса (метод виключення) грунтується на доведенні матриці коефіцієнтів системи (2.1) до трикутного вигляду:

і складається з двох етапів: прямого ходу і зворотного підставлення. Етап прямого ходу закінчується, коли одне з рівнянь системи стає рівнянням з одним невідомим. Далі, здійснюючи зворотне підставлення, знаходять всі невідомі. З метою зменшення обчислювальної похибки використовують метод Гаусса з вибором головного елементу. Під головним елементом будемо розуміти максимальний по модулю елемент матриці А, обраний по заданій множині рядків та стовпців. Алгоритм методу полягає у наступному.

Спочатку знаходиться головний елемент матриці А і шляхом перестановки рівнянь та стовпців він розміщується на місці елемента (перестановку стовпців потрібно запам’ятовувати для вірного співставлення змінних з отриманими значеннями). Потім ділимо перше рівняння на , після чого воно отримує вигляд:

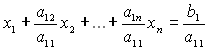                                   (2.2)

Помножимо послідовно (2.2) на а₂₁, а₃₁, …, а_n1 та віднімемо відповідно з 2-го, … , n-го рівняння системи. Отримаємо СЛАР А¹х=В¹:

.

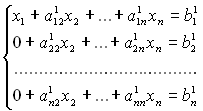Її елементи розраховані за формулами:

і для , .

Нехай на деякому кроці отримано матриці А^к і В^к (початкові матриці відповідають А⁰ і В⁰), а діагональний елемент а_{к+1, к+1}^к – максимальний по модулю елемент матриці А^к по рядкам i>k і стовпцям j>k (при необхідності переставляються відповідні рівняння чи стовпці).

Наведемо формули для розрахунку матриць А^к+1 і В^к+1:

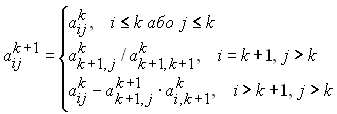,          (2.3)

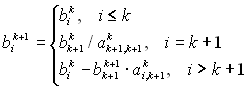.                    (2.4)

При програмуванні методу для зберігання інформації про коефіцієнти матриць достатньо використовувати один двомірний масив з n рядками та n+1 стовпцем, в якому розміщується розширена матриця системи .

Умови завершення прямого ходу метода Гаусса.

При виконанні розрахунків може виникнути проблема: елемент . Ця ситуація виникає, коли всі елементи матриці А^к по рядках i>k дорівнюють нулю. Система в цьому випадку має вигляд:

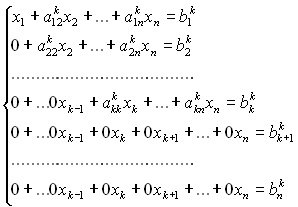
Застосування формул (2.3), (2.4) неможливе. В даному випадку система має безкінечну множину розв’язків, або не має їх зовсім. Це визначається по матриці В^к.

Якщо всі елементи b_i^k = 0 при i ≥k+1, то система має безкінечну множину розв’язків, причому корені х₁,…, х_к називаються залежними і виражають через значення х_к+1,…,x_n, які називают незалежними коренями.

Якщо хоч один елемент b_i^{k №} 0 при i ≥ k+1, то розв’язків у системи немає.

У випадку, коли проблеми ділення на нуль не виникало і була отримана трикутна матриця Аⁿ, система має єдиний розв’язок. Для його пошуку застосовується зворотній хід метода Гаусса:

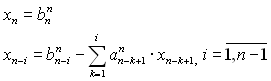.               (2.5)

Число арифметичних операцій для реалізації методу

.

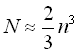Алгоритм методу наведений на рисунку 2.1. Приклад розв’язку СЛАР методом Гаусса наведено у Додатку А( 2 том посібника).