2.1.1.2 Метод виключення Гаусса-Жордана

Цей метод дозволяє привести матрицю коефіцієнтів до діагонального вигляду. Єдиною його формальною відмінністю від попереднього методу є те, що замість підставляється (-й ряд називається провідним). В методі Гаусса перетворення торкалися тільки рівняння, що стоять нижче провідного ряду. Від класичного методу Гаусса цей метод відрізняється тим, що пронормований рядок віднімається не тільки від нижніх, а й від верхніх рівнянь системи, в результаті чого матриця А зводиться до одиничної. Зворотній хід в такому разі не потрібен, розв’язком системи буде стовпець Вⁿ. Метод Гаусса-Жордана можна використовувати з вибором головного елементу чи без. Пошук головного елементу відбувається аналогічно попередньому методу. Формули (2.3), (2.4) з вказаними змінами будуть мати вигляд:

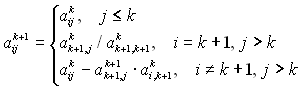,               (2.6)

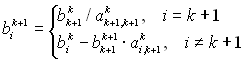.                    (2.7)

Цей метод полегшує одержання розв’язку, але супроводжується збільшенням обсягу обчислень.

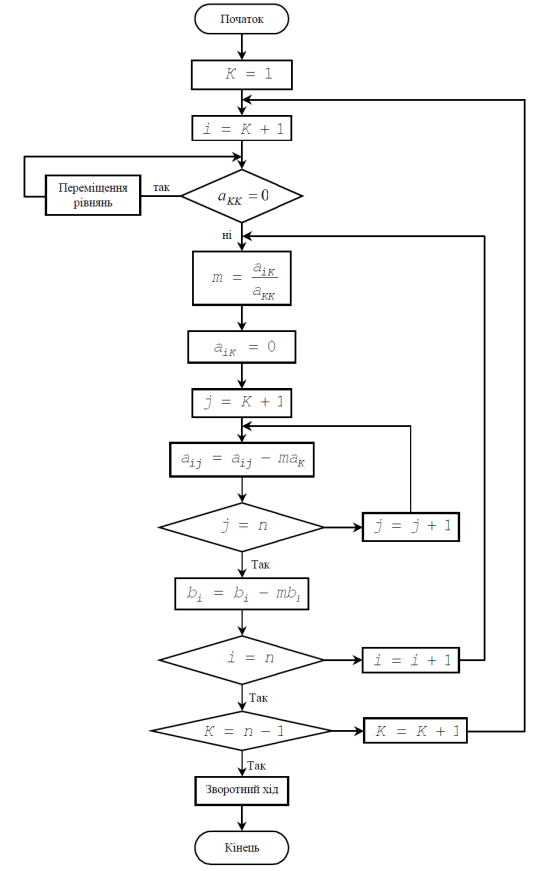
Рисунок 2.1 – Алгоритм методу Гауса