
2.1.1.3 Модифікований метод Гаусса
У багатьох випадках виникає необхідність розв’язання систем лінійних рівнянь із матрицею коефіцієнтів, яка змінюється, і постійним стовпцем вільних членів. Найчастіше для розв’язання таких задач використовується модифікований метод Гаусса. В цьому методі матрицю коефіцієнтів ![]() з матричного рівняння (2.1) подають у вигляді добутку лівої і правої трикутних матриць
з матричного рівняння (2.1) подають у вигляді добутку лівої і правої трикутних матриць
![]() .
.
Оскільки діагональні елементи однієї з матриць дорівнюють одиниці, їх можна не запам’ятовувати, і обидві матриці зберігати в пам’яті ЕОМ на місці матриці коефіцієнтів.
У варіанті методу, що називається методом Краута, використовується така послідовність знаходження елементів матриць:
![]()
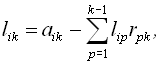
![]() ;
;

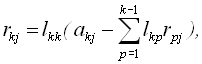
![]() ;
;
![]() .
.
Система ![]() зводиться до системи
зводиться до системи ![]() , розв’язання якої замінюється розв’язанням двох систем з трикутними матрицями:
, розв’язання якої замінюється розв’язанням двох систем з трикутними матрицями:
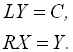
Елементи ![]() знаходять з таких співвідношень:
знаходять з таких співвідношень:
![]()
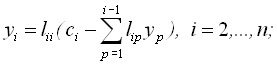
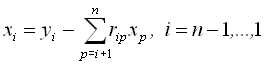 .
.
Число арифметичних операцій, необхідних для розв’язання цим методом системи лінійних алгебраїчних рівнянь, ![]() .
.
Алгоритм модифікованого методу Гауса переставлено на рис.2.2
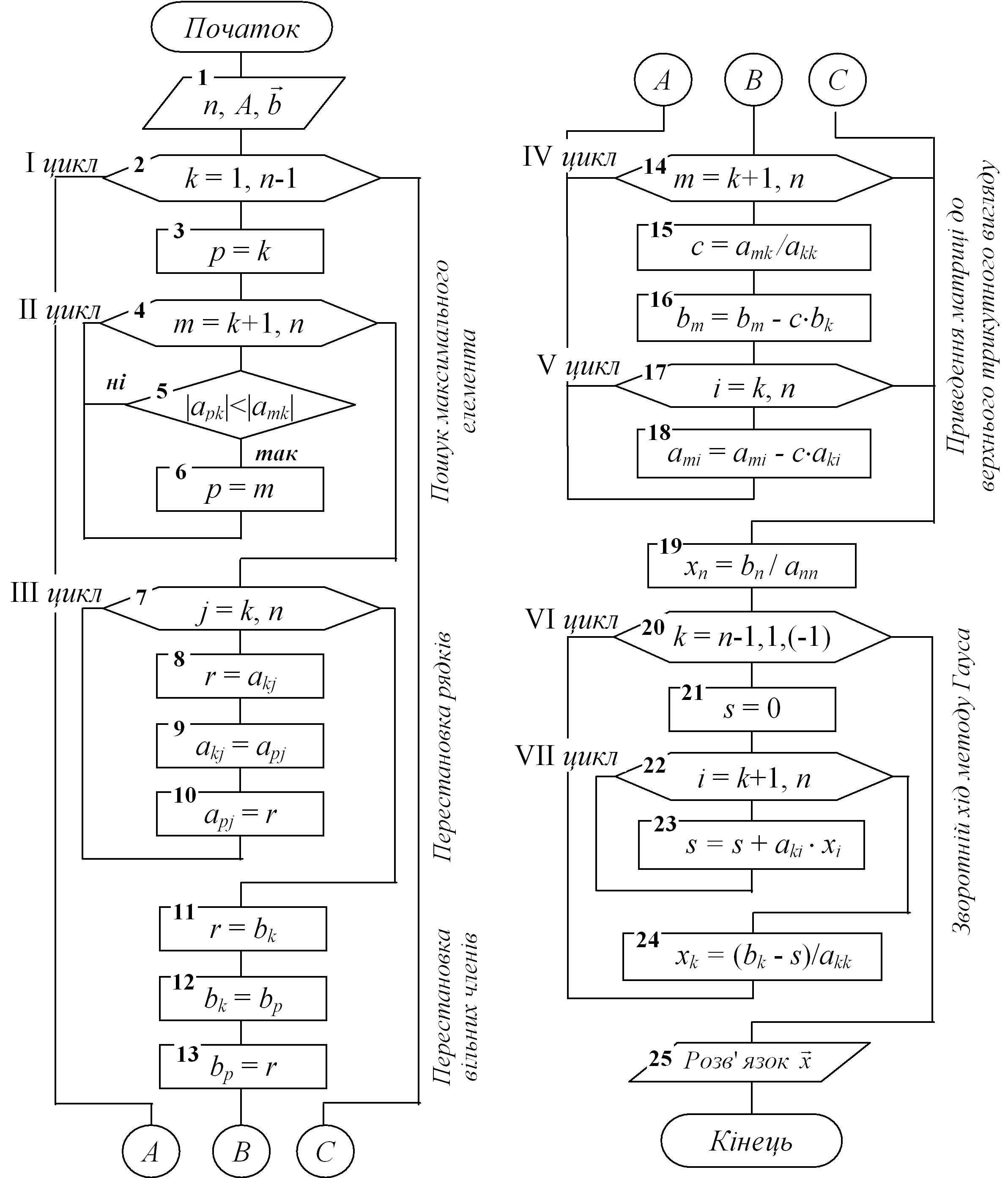
Рисунок 2.2 – Алгоритм модифікованого методу Гаусса