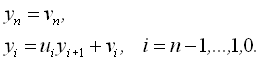Перший спосіб ґрунтується на використанні тієї властивості визначників, що визначник матриці дорівнює сумі добутків елементів будь-якого рядка чи стовпця на їх алгебраїчне доповнення, тобто:

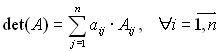
Таким чином, обчислення одного визначника n-го порядку зводиться до розрахунку n визначників порядку n-1. Реалізується даний спосіб за допомогою рекурсії.

Рекурсивний спосіб зручно застосовувати по відношенню до рядків чи стовпців, що мають велику кількість нульових елементів. Якщо ж нульових елементів у матриці немає або дуже мало, то застосування цього способу є вкрай не ефективним. Для визначника n порядку доведеться розрахувати n!/2 визначників другого порядку.

Метод, що базується на алгоритмові прямого ходу метода Гаусса, використовує властивість визначника трикутної матриці. Для такої матриці визначник дорівнює добутку елементів головної діагоналі.

Для обчислення визначника використовується алгоритм побудови послідовності матриць А?А¹?А²?…?Аⁿ прямого ходу метода Гаусса з тією відмінністю, що при перестановці рядків чи стовпців знак визначника змінюється на протилежний. Значення визначника розраховується по формулі:

,

де m – кількість перестановок.

Цей метод дозволяє обчислювати визначники матриць великих порядків.

2.1.1.5 Метод Крамера

Даний метод полягає у розрахунку визначника det(A) матриці А, а також визначників det(А_k) матриць А_k, . Матриці А_k отримуються з матриці А шляхом заміни k-го стовпця на стовпець В.

Можливі наступні варіанти:

1. Якщо detA?0, то система має єдиний розв’язок , який знаходиться за формулою:

.

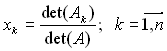2. Якщо det(A)=0 та всі det(А_k)=0, , то розв’язків у системи безкінечна множина.

3. Якщо det(A)=0 і хоч би один det(А_k) ?0, то розв’язку у системи немає.

Метод Крамера (визначників) не може бути застосований в більшості практичних задач через велику складність розрахунку визначників, навіть при невеликому зростанні порядку системи.

Приклад розв’язку СЛАР методом Крамера наведено у Додатку А.

2.1.1.6 Метод оберненої матриці

Якщо задача розв’язку СЛАР вирішується у пакеті прикладних програм, в якому реалізована функція обчислення оберненої матриці, то для пошуку розв’язку можна застосовувати формулу:

,

де – обернена матриця.

Нагадаємо визначення оберненої матриці. Оберненою до квадратної матриці А називається така матриця , для якої виконується співвідношення:

А·А^-1=Е=А^-1·А,

де Е – одинична матриця.

2.1.1.7 Метод прогонки

Метод прогонки застосовується для розв’язання систем рівнянь з стрічковими матрицями коефіцієнтів. Розглянемо його застосування для розв’язання тридіагональної системи, до якої часто зводиться лінійна крайова задача.

Запишемо систему в такому вигляді:

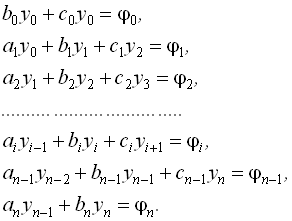
Для розв’язання цієї системи виконаємо аналог прямого ходу методу Гаусса. Тоді одержимо систему у вигляді

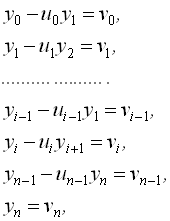
де – деякі коефіцієнти, що називаються прогоночними.

Bідзначимо, що

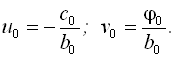
Прогоночні коефіцієнти, визначені із останньої системи, дають можливість знайти .

Виключаючи із попередніх співвідношень шляхом арифметичних перетворень, одержуємо формули визначення шуканих значень:

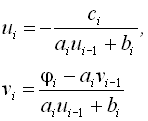
і далі