
2.1.2 Ітераційні методи
Ітераційні методи особливо ефективні при високому порядку системи. Вони застосовуються в системах, попередньо приведених до вигляду:
 (2.8)
(2.8)
або в матричній формі: ![]()
де 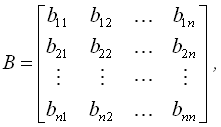
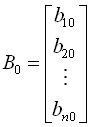 .
.
Існує декілька основних різновидів ітераційних методів. Це методи Якобі (простої ітерації), Гаусса – Зейделя і послідовної верхньої релаксації, в основі яких лежить систематичне уточнення значень змінних, заданих на початку розрахунку.
В методі Якобі початкові значення змінних використовуються для обчислення нових значень ![]() за допомогою наведених нижче рівнянь. Процес припиняється, коли всі нові значення виявляються достатньо близькими до початкових. В протилежному випадку нові значення використовуються замість початкових. Ця процедура повторюється доти, доки не буде досягнута збіжність або стане ясно, що процес розбіжний. В цьому методі заміна значень всіх змінних проводиться одночасно (одночасне зміщення).
за допомогою наведених нижче рівнянь. Процес припиняється, коли всі нові значення виявляються достатньо близькими до початкових. В протилежному випадку нові значення використовуються замість початкових. Ця процедура повторюється доти, доки не буде досягнута збіжність або стане ясно, що процес розбіжний. В цьому методі заміна значень всіх змінних проводиться одночасно (одночасне зміщення).
Система ітераційних рівнянь має вигляд:

де ![]() , відповідно, значення,
, відповідно, значення, ![]() на наступній (m+1) і попередній (m) ітераціях.
на наступній (m+1) і попередній (m) ітераціях.
В методі Гаусса-Зейделя уточнене значення ![]() відразу ж використовується для обчислення
відразу ж використовується для обчислення ![]() . Потім по нових значеннях
. Потім по нових значеннях ![]() і
і ![]() визначаються
визначаються ![]() і т.д. Це дозволяє істотно збільшити швидкість збіжності.
і т.д. Це дозволяє істотно збільшити швидкість збіжності.
В методі послідовної верхньої релаксації нові значення кожної змінної обчислюються як:
![]() ,
,
де ![]() – уточнене значення
– уточнене значення ![]() за методом Гаусса-Зейделя;
за методом Гаусса-Зейделя; ![]() –параметр релаксації (
–параметр релаксації (![]() ).
).
При ![]() цей метод подібний до методу Гаусса-Зейделя. Швидкість збіжності залежить від
цей метод подібний до методу Гаусса-Зейделя. Швидкість збіжності залежить від ![]() .
.
Одним з головних питань щодо застосування ітераційних методів є збіжність. Для оцінки збіжності обчислюються норми матриці коефіцієнтів ![]() з системи (2.2).
з системи (2.2).
Найбільшого поширення набули такі способи оцінки норм:
І норма :  ,
,
ІІ норма : 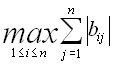 ,
,
![]() -норма (Евклідова) :
-норма (Евклідова) : 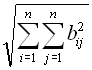 .
.
Існує декілька підходів до визначення збіжності за допомогою оцінки норм. В загальному випадку достатньо, щоб хоча б одна з норм матриці В була менша за одиницю
||B||<1.
В математиці називають таку умову “звичайною” або “сильною”. В багатьох випадках збіжність забезпечується і при виконанні так званої “слабкої” ознаки. Наприклад, “слабка” ознака сум по рядках: для всіх сум коефіцієнтів рядків ![]() виконується співвідношення:
виконується співвідношення:

але є один рядок ![]() для якого
для якого
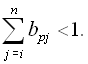
Аналогічно визначається “слабка” ознака сум по стовпцях.
“Слабка ” ознака може використовуватися в тих випадках, коли матриця коефіцієнтів А системи рівнянь (2.1) є нерозкладна, тобто це квадратна матриця А, яку (на відміну від розкладної) не можна привести до вигляду:
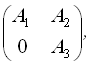
де ![]() - квадратні матриці.
- квадратні матриці.
Для розкладних матриць система рівнянь (2.1) розпадається на дві системи рівнянь, що вирішуються послідовно. В більш детальних підручниках, список яких наведено в кінці цієї книги, міститься багато більш детальних доведень і аналіз властивостей та ознак для оцінки збіжності, але для загальноінженерного підходу до багатьох практичних задач достатньо даних, що наведені вище.