
2.2 Визначення власних значень матриць
2.2.1 Постановка проблеми
Багато інженерних задач зводяться до розгляду систем рівнянь, що мають єдиний розв’язок лише в тому разі, якщо відомо значення деякого внутрішнього параметра. Цей особливий параметр називають характеристичним або власним параметром (значенням) системи. При аналізі автоматичних систем власні значення дозволяють визначити критичні параметри керувальних впливів, перевищення яких призводить до втрати стійкості системою. При динамічному аналізі механічних або радіоелектронних систем з самозбудженням власні значення відповідають резонансним частотам коливань, а власні вектори характеризують амплітуди цих коливань.
Формулювання проблеми:
Знайти ![]() скалярних значень
скалярних значень ![]() і власних векторів
і власних векторів ![]() , що задовольняють матричне рівняння
, що задовольняють матричне рівняння
![]() (2.3)
(2.3)
Разом з пересічною проблемою власних значень існує так звана узагальнена проблема власних значень (задача для двох матриць ![]() і
і ![]() ):
):
![]() .
.
Тут ми розглянемо тільки ту проблему, що виникає з рівняння (2.3).
Згадаємо деякі визначення з теорії матриць:
-
квадратна матриця
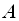 називається особливою (сингулярною), якщо
називається особливою (сингулярною), якщо
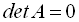 ;
; -
матриця
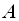 називається ортогональною, якщо
називається ортогональною, якщо
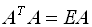 ,
,тобто
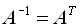 , де
, де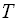 - знак транспонування;
- знак транспонування; -
матриці
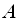 і
і
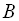 подібні, якщо існує така несингулярна матриця
подібні, якщо існує така несингулярна матриця
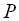 , що справедливо співвідношення
, що справедливо співвідношення
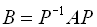 .
.Доцільно перед аналізом методів визначення власних значень зупинитись на властивостях власних значень і векторів:
1. Всі
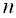 власних значень симетричної матриці розміру
власних значень симетричної матриці розміру
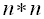 , що складається з дійсних чисел, дійсні.
, що складається з дійсних чисел, дійсні.2. Якщо власні значення матриці різні, то її власні вектори ортогональні. Сукупність
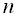 лінійно незалежних власних векторів складає базис простору, що розглядається. Тому для сукупності лінійно незалежних векторів
лінійно незалежних власних векторів складає базис простору, що розглядається. Тому для сукупності лінійно незалежних векторів
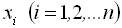 будь-який вектор в тому ж просторі можна виразити через власні вектори.
будь-який вектор в тому ж просторі можна виразити через власні вектори.3. Якщо дві матриці подібні, то їх власні значення збігаються. З подібності
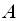 і
і
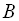 виходить, що
виходить, що
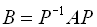 , оскільки
, оскільки
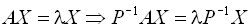 . Якщо прийняти
. Якщо прийняти
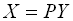 , тоді
, тоді
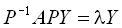 , тобто
, тобто
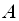 і
і
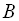 не тільки мають однакові
не тільки мають однакові
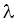 , але і їх власні вектори зв’язані співвідношенням
, але і їх власні вектори зв’язані співвідношенням
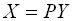 .
.4. Добуток власного вектора матриці на скаляр, є власним вектором тієї ж матриці. Як правило, власні вектори нормалізують, розділивши їх на найбільший елемент або на суму квадратів елементів.
2.2.2 Методи обчислення власних значень
Вибір найбільш ефективного методу визначення власних значень або власних векторів для заданої задачі залежить від ряду факторів (тип рівнянь, число і характер власних значень, вид матриці і т.д.). Алгоритми визначення власних значень можна розподілити на 3 групи:
2.2.2.1 Прямі методи
Найбільш очевидним шляхом розв’язання задач на власні значення є їх визначення з системи рівнянь, яка має ненульовий розв’язок лише в разі, коли ![]()
Розв’язання в цьому випадку складається з двох етапів:
- розгорнення вікового визначника безпосередньо або одним з відомих методів: Данілевського, Крилова, Леверрьє, невизначених коефіцієнтів, інтерполювання і т.д.;
- розв’язання одержаного характеристичного рівняння, корені якого і будуть власними значеннями матриці. Для визначення коренів можна використати один з методів розв’язання нелінійних алгебраїчних рівнянь(див.гл.3).
В таблиці 2.1 наведені результати порівняння ефективності різних методів розгортання вікових визначників, де критерієм є кількість обчислювальних операцій, а в таблиці 2.2 порівняння методів розв’язання з точки зору складності, точності та швидкості збігання. Більш детальний опис цих методів можна знайти в підручниках, список яких наведено в кінці книги.
Таблиця 2.1
Кількість дій, що використовуються різними методами розгортання вікового визначника в залежності від його порядку.
Таблиця 2.2
Вибір алгоритму розв’язання задачі на власні значення
Назва алгоритму |
Застосову ється для матриць |
Результат |
Рекомендується для пошуку власних значень |
Примітка |
Max або min |
Всі x<6 |
Всі х>=6 |
Визнач- ник (ітерація) |
Загального вигляду |
Власні значення |
х |
Потребує знаходження коренів полінома загального вигляду |
||
Ітерація (ітерація) |
Загального вигляду |
Власні значення і власні вектори |
х |
х |
х |
Забезпечує найкращу точність для найбільшого і найменшого власних значень |
Метод Якобі (перетво- рення) |
Симетрич- них |
Діагональ на форма матриці |
х |
х |
Теоретично потребує нескінченного числа кроків |
Метод Гівенса (перетво- рення) |
Симетрич- них |
Тридіагональна форма матриці |
х |
х |
Потребує знання коренів простого полінома |
Несимет- ричних |
Форма Гессенбер га |
х |
х |
Потребує застосування додаткового методу |
||
Метод Хаусхол- дера (перетво- рення) |
Симетрич- них |
Тридіа- Гональна форма матриці |
х |
х |
Потребує знання коренів простого полінома |
|
Метод LR (перетво- Рення) |
Загального вигляду |
Квазідіаго-нальна форма матриці |
х |
х |
Буває нестійкий |
|
Метод QR (перетво- Рення) |
Загального вигляду |
Квазідіаго-нальна форма матриці |
х |
х |
Найкращий метод, що має найбільшу узагальненість |
2.2.2.2 Ітераційні методи
Ітераційні методи (Iteration methods) основані на багатократному використанні ітераційного алгоритму, що наближає власний вектор, який одержується в кожному циклі, до точного розв’язку.
Розрахунок починається зі початкового нормованого вектору ![]() , який множиться зліва на матрицю
, який множиться зліва на матрицю ![]() , і результат дорівнює добутку постійної (власне значення
, і результат дорівнює добутку постійної (власне значення ![]() ) і нормованого вектору
) і нормованого вектору ![]() :
:
![]() .
.
Якщо вектор ![]() збігається з
збігається з ![]() , то розрахунок припиняється. Інакше вектор
, то розрахунок припиняється. Інакше вектор ![]() використовується в якості початкового, і всі обчислення повторюються доти, доки
використовується в якості початкового, і всі обчислення повторюються доти, доки ![]() , де
, де ![]() і
і ![]() – в ектори, що одержані в
– в ектори, що одержані в ![]() і
і ![]() ітераційних циклах, а
ітераційних циклах, а ![]() – задана припустима похибка обчислень.
– задана припустима похибка обчислень.
Якщо процес збігається, одержаний постійний множник відповідає найбільшому власному значенню ![]() , а нормований вектор – відповідному власному вектору.
, а нормований вектор – відповідному власному вектору.
Аналогічно можна знайти найменше власне значення. Для цього початкова система рівнянь попередньо множиться на обернену матрицю ![]() :
:
![]() ,
,
звідки одержуємо 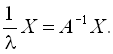
Подальше розв’язання задачі на власні значення за алгоритмом рисунку2.1 приводить до максимального власного значення 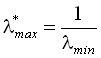 , за яким знаходиться найменше власне значення
, за яким знаходиться найменше власне значення ![]() .
.
Визначивши максимальне або мінімальне власне значення, можна знайти наступні за ним за величиною, замінивши вихідну матрицю матрицею, яка містить лише решту власних значень.
Принцип ортогональності власних векторів ![]() при
при ![]() і
і ![]() при
при ![]() дозволяє довести твердження, що якщо створити нову матрицю
дозволяє довести твердження, що якщо створити нову матрицю ![]() , то вона буде мати власне значення
, то вона буде мати власне значення ![]() , а всі решта її власних значень будуть збігатися з власними значеннями вихідної матриці
, а всі решта її власних значень будуть збігатися з власними значеннями вихідної матриці ![]() . В результаті знаходимо
. В результаті знаходимо ![]() і далі, утворюючи
і далі, утворюючи ![]() і т.д., аналогічно визначаємо всі власні значення і вектори.
і т.д., аналогічно визначаємо всі власні значення і вектори.