2.2.2.3 Методи перетворень подібності

 

Методи перетворень подібності основані на властивостях подібних матриць, які мають однакові власні значення і ортогональні власні вектори.

Ці методи використовуються для одержання з вихідної матриці нової, подібної до неї, але простішого вигляду. Очевидно, найкращим спрощенням було б приведення матриці до діагонального (або блочно - діагонального) вигляду. В цьому випадку власні значення відповідали б елементам матриці, що стоять на головній діагоналі (в випадку дійсних власних значень), або просто визначались би з квадратних матриць розміру 2 х 2 ( в випадку комплексних), що стоять на головній діагоналі. Приведення до діагонального вигляду часто важко здійснити, тому в результаті більшість методів приводить матрицю до тридіагонального вигляду, для якого існують достатньо добре досліджені і відпрацьовані на практиці методи знаходження власних значень. Як приклад можна навести метод, що приводить до послідовності Штурма і має таку властивість, що корені полінома -го порядку розташовуються між коренями поліномів -го порядку (це значно спрощує їх визначення, оскільки обмежує ділянки відокремлення коренів). Вихідний визначник тридіагональної матриці

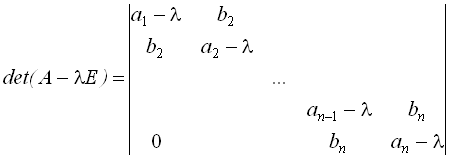
може бути представлений послідовністю поліномів Штурма

,

за умови і .

Приймаючи і послідовно визначаючи корені, знаходимо власні значення як корені поліному порядку.

Якщо в разі симетричних матриць ефективним способом знаходження власних значень є приведення матриці до тридіагонального вигляду, то для симетричних матриць доцільно користуватися методами перетворення подібності для приведення вихідної матриці вигляду Гессенберга:

Для приведення матриць до тридіагонального вигляду (або вигляду Гессенберга) існує ряд методів, найбільш відомими з яких є методи Якобі, Гівенса, Хаусхолдера, які докладно розглядаються в спеціальній літературі. Переваги має (з точки зору швидкодії і кількості обчислювальних операцій) метод відображень, що запропонований Хаусхолдером. Цей метод дозволяє при виконанні одного кроку перетворень перетворити в нуль одразу всі елементи цілого рядка і стовпця, що стоять зовні трьох діагоналей, в той час як в методі Гівенса на кожному -му кроці для цього необхідно зробити перетворень, а в методі Якобі створення нового нульового елементу може супроводжуватись його зникненням в іншому місці матриці, тобто не гарантовано одержання результату за кінцеву кількість кроків.

Найбільш загальними з методів перетворень подібності є методи і , що основані на представленні матриці в вигляді добутків і , де - ліва трикутна матриця з одиничними діагональними елементами; - права трикутна матриця; - ортогональна матриця.

Далі, застосовуючи перетворення подібності

,

одержуємо послідовність матриць, яка прямує до квазідіагонального вигляду.

 

2.2.3 Порівняння методів визначення власних значень

 

Основними критеріями, що дозволяють оцінити ефективність методів знаходження власних значень, стосовно їх алгоритмізації і використання для розв’язання задач на ЕОМ, є точність, швидкодія (кількість обчислювальних операцій) і необхідний розмір пам’яті ЕОМ.

Швидкодія методу залежить від двох складових: кількості операцій в єдиному циклі і кількості циклів, необхідних для одержання результату.

Важливим критерієм оцінки методів визначення власних значень є їх загальність (універсальність), тобто пристосованість до матриць різних видів, незалежно від симетрії і вигляду елементів (дійсні або комплексні).

Проаналізуємо з точки зору цих критеріїв методи знаходження власних значень.

Прямі методи приводять до необхідності розв’язання нелінійних алгебраїчних рівнянь. Методи їх розв’язання достатньо добре розроблені. Але в задачах на власні значення часто зустрічаються кратні корені, при цьому ітераційні методи не гарантують одержання розв’язку. Швидкодія цих методів різко зменшується при підвищенні порядка матриці внаслідок розкриття вікового визначника.

Ці недоліки ускладнюють використання прямих методів знаходження власних значень для великих матриць (порядку більше 10).

Істотним недоліком ітераційних методів розв’язання задач знаходження власних значень є накопичення помилок при кожному кроці ітераційного процесу (при визначенні максимального значення, створенні нової матриці і т.д.), тому практично ними можна користуватися для визначення не більше трьох-чотирьох власних значень.

В інших випадках доцільно користуватись методами перетворення подібності.

Найбільш ефективні методи перетворення подібності гарантують одержання результату при достатньо високій точності розв’язку. Часто найефективніший розв’язок задачі забезпечується при одночасному використанні декількох методів перетворення подібності. Наприклад, методом Хаусхолдера матриця приводиться до вигляду Гессенберга, а потім методом визначаються власні значення.

Таким чином, вибір найбільш зручного алгоритму для розв’язання різних задач знаходження власних значень визначається типом власних значень, виглядом матриці і кількістю шуканих власних значень. Чим більш складна задача, тим менше методів та алгоритмів, з яких можна вибирати. Найбільш універсальний алгоритм , але він і один з найскладніших. При малих порядках матриці можна користуватись найпростішими прямими і ітераційними методами, а при збільшенні порядку і ускладненні вигляду матриці рекомендуються лише методи перетворення подібності. Таблиця2.2 дозволяє полегшити вибір методу розв’язання задачі на власні значення. Звичайно пакети математичного забезпечення ЕОМ містять програми, в яких використовується більшість з цих алгоритмів. Одним з ефективних засобів використання наявних ресурсів ЕОМ є одночасне застосування двох підпрограм, що дозволяє поєднати їх найкращі якості.

 

Контрольні запитання та завдання

1. Чим відрізняються прямі та непрямі методи розв’язання систем лінійних рівнянь? Дати порівняльну оцінку.

2. Розкрити суть методів Крамера, Гаусса (і його різновидів), прогонки.

3. Як подається система рівнянь для застосування ітераційних методів?

4. Як перевірити збіжність ітераційних алгоритмів?

5. Чим відрізняються алгоритми ітераційних методів Якобі, Гаусса – Зейделя, послідовної верхньої релаксації ?

6. Розв’язати наведену нижче систему рівнянь методом Крамера. Скласти алгоритм і програму розв’язання.

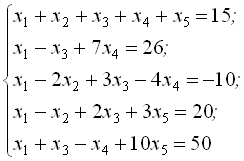
7. Розв’язати систему рівнянь з прикладу 6 методом Гаусса. Скласти алгоритм і програму.

8. Розв’язати систему рівнянь з прикладу 6 методом Гаусса-Жордана. Скласти алгоритм і програму.

9. Розв’язати систему рівнянь з прикладу 6 модифікованим методом Гаусса. Скласти алгоритм і програму.

10. Чи можна розв’язати систему рівнянь з прикладу 6 методом прогонки? Скласти алгоритм і програму для розв’язання методом прогонки системи з n рівнянь та тридіагональною матрицею коефіцієнтів.

11.     Розв’язати вказаними в п. 6, 7, 8, 9, 10 методами на ЕОМ таку систему:

11.1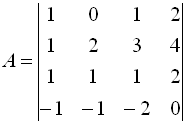

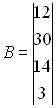
11.2

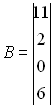
11.3

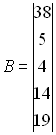
12.     Розв’язати методом Якобі наведену нижче систему. Скласти алгоритм і програму. Перевірити збіжність.

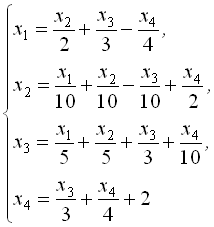
13. Розв’язати методом Гаусса-Зейделя систему з п. 12. Скласти алгоритм і програму. Перевірити збіжність

14. Розв’язати методом послідовної верхньої релаксації систему з п. 12 з параметром релаксації

15. Сформулювати проблему визначення власних значень матриці.

16. Яка матриця називається несингулярною?

17. Сформулюйте умову ортогональності матриці.

18. Назвіть властивості власних значень та векторів.

19. Чим відрізняються прямі та ітераційні методи визначення власних значень та векторів?

20. Визначити прямим методом власні значення та вектори матриць:

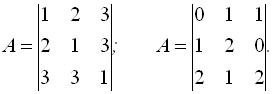
21. Скласти алгоритм, програму та визначити власні значення матриць з п. 20 ітераційним методом.

22. Дати загальну характеристику методів перетворень подібності.

23. Чим відрізняються LQ та QR методи ?

24. Дати порівняльну оцінку, аналіз ефективності та умов застосування різних методів визначення власних значень та векторів.