Розділ 3 Нелінійні задачі

 

В цьому розділі розглянуті методи розв’язання нелінійних рівнянь та систем рівнянь. До них зводиться багато практичних задач, наприклад, розрахунки нелінійних електричних кіл та систем керування, розв’язання нелінійних диференціальних рівнянь, аналіз стійкості систем шляхом оцінки їх власних значень та ін.

Якщо для найпростіших видів алгебраїчних рівнянь (не вище третього степеня) існують точні аналітичні формули, то для трансцендентних рівнянь і будь-яких систем рівнянь таких методів взагалі не існує і слід користуватися тільки наближеними ітераційними методами та алгоритмами, найбільш поширені з яких розглянуто нижче.

 

3.1 Розв’язання нелінійних рівнянь

 

Рівняння, в які входять тільки степені аргументу з відповідними коефіцієнтами, називаються алгебраїчними.

Загальний вигляд алгебраїчного рівняння:

     .     (3.1)

Нелінійні рівняння, що містять тригонометричні, експоненціальні, логарифмічні або інші спеціальні функції, називаються трансцендентними. Наприклад, трансцендентне рівняння може мати вигляд:

Геометричний сенс розв’язку рівняння f(x) = 0, як алгебраїчного, так і трансцендентного, полягає у знаходженні точки перетину графіку функції f(x) з віссю ОХ.

Можна виділити деякі важливі властивості алгебраїчних рівнянь, що спрощують визначення коренів. Тут і далі ми називаємо деякі властивості теоремами, як це прийнято в математиці, але наводимо їх без доведень, щоб не ускладнювати сприйняття матеріалу. За власним бажанням, можна довести ці теореми в якості додаткових самостійних завдань. З метою полегшення розуміння матеріалу нагадуємо необхідні визначення.

Функція f(х) неперервна в точці х₀ ,якщо . Функція f(х) неперервна на відрізку [a,b], якщо вона неперервна в будь-якій точці цього відрізку.

Похідною функції f(х) в точці х₀ називають:

.

Якщо функція має похідну в точці, то вона неперервна в ній. Обернене твердження не є вірним.

Функція f(х) монотонна на відрізку [a,b], якщо її похідна має однаковий знак (>0 або <0) на усьому відрізку [a,b].

Функція f(х) опукла (ввігнута) в точці х₀, якщо її друга похідна f''(x₀)()0.

1. ОСНОВНА ТЕОРЕМА АЛГЕБРИ. Алгебраїчне рівняння порядку n має n коренів, які можуть бути як дійсними, так і комплексними.

Кожен корінь рахується відповідну кількість разів, що дорівнює його кратності. Кратність кореня рівняється , якщо

.

2. Якщо всі коефіцієнти рівняння (3.1) дійсні, то всі комплексні корені утворюють комплексно-спряжені пари.

3.ТЕОРЕМА ДЕКАРТА. Число позитивних дійсних коренів дорівнює або менше за число змін знаків в послідовності коефіцієнтів (те ж твердження справедливе відносно числа від’ємних дійсних коренів при заміні в (3.1) на -).

4. ТЕОРЕМА ЛАГРАНЖА. Верхня межа позитивних дійсних коренів визначається як

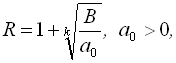
де – номер першого від’ємного коефіцієнта; – найбільша абсолютна величина від’ємного коефіцієнта.

5. ТЕОРЕМА ГЮА. Якщо рівняння (3.1) має дійсні корені і дійсні коефіцієнти, то

Нагадаємо, що прямі аналітичні методи існують лише для алгебраїчних рівнянь не вище третього порядку, а для трансцендентних рівнянь прямих методів взагалі не існує. При визначенні дійсних коренів чисельними методами треба враховувати три теореми. Перші дві дозволяють відокремити корені, тобто встановити якомога тісніші інтервали , в яких знаходиться один і тільки один корінь рівняння, а третя – оцінити ступінь наближення.

ТЕОРЕМА 1. Якщо безперервна функція приймає значення різних знаків на кінцях відрізка , тобто , то в середині цього відрізка міститься щонайменше один корінь рівняння , тобто знайдеться хоча б одне число таке, що .

ТЕОРЕМА 2. Якщо монотонна функція приймає значення різних знаків на кінцях відрізка , тобто , то на цьому відрізку міститься рівно один корінь рівняння .

ТЕОРЕМА 3. Нехай - точний, а - наближений корені рівняння , які знаходяться на одному й тому ж відрізку , причому .

Тоді

.

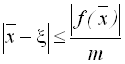Розв’язок нелінійних рівнянь складається з двох етапів:

На першому етапі необхідно знайти відрізок [a,b], на якому функція має рівно один нуль (відділення коренів).

На другому етапі відбувається уточнення кореня на знайденому відрізку за допомогою одного з чисельних методів з заданою точністю.

Відділити корінь х* рівняння f(x) = 0 – значить вказати окіл точки x*, який не містить інших коренів цього рівняння.

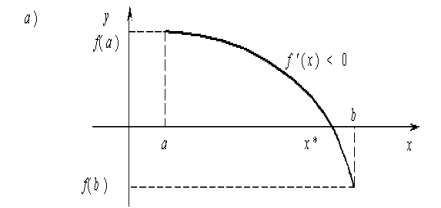
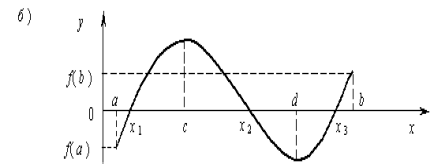
Рисунок 3.1 – Відділення коренів рівняння

 

Якщо безперервна функція f(x) на кінцях відрізка [a, b] приймає значення різних знаків, тобто якщо f(a) f(b) < 0, то всередині цього відрізка існує, принаймні, один корінь рівняння f(x) = 0 (рис 3.1). При цьому корінь x* буде єдиним, якщо f '(x) зберігає знак усередині інтервалу [а, b] (рис. 3.1а).

На практиці відділення кореня рівняння f(x) = 0 на відрізку [а,b] починається з перевірки умови f(a) f(b) < 0. Якщо ця умова виконана, то на [а, b] є корінь і подальше завдання полягає в з'ясуванні його одиничності або не одиничності.

Для відділення коренів практично досить провести процес половинного розподілу, відповідно до якого відрізок [a, b] ділиться на 2,4,8,... рівних частин і послідовно визначаються знаки функції в точках поділу. При цьому якщо в точках поділу виконується умова , то на інтервалі є корінь рівняння f(x) = 0. При визначенні коренів завжди намагаються знайти інтервал як можна меншої довжини.

Графічне відділення коренів рівняння полягає в знаходженні абсциси точки перетину графіка y = f(x) з прямою у = 0, тобто віссю абсцис. При цьому, якщо побудувати графік y = f(x) складно, то функцію представляють в еквівалентному вигляді:

f₁(x) = f₂(x)

з таким розрахунком, щоб графіки y₁ = f₁(x) і y₂ = f₂(x) було простіше побудувати. Абсциси їх точок перетину будуть коренями рівняння. При графічному відділенні коренів рівняння, результат залежить від точності побудови графіків.

Існує ряд методів наближеного розв’язання нелінійних рівнянь, доцільність застосування кожного із яких визначається видом рівняння, його порядком, потрібною точністю і т.д. При розгляді методів будемо вважати, що корені вже відділені.

Слід також пам’ятати, що при визначенні великої кількості коренів знижувати степінь початкового нелінійного рівняння шляхом ділення на (де х_i – знайдений корінь) треба дуже обережно, що пов’язано з накопиченням похибки розповсюдження, яка буде в коефіцієнтах нового рівняння.