3.2 Розв’язання систем нелінійних рівнянь

 

В загальному випадку система з n нелінійних рівнянь з n невідомими подається у вигляді:

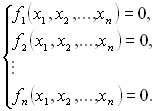     (3.10)

Оскільки нелінійні функції, що входять до системи, неможливо описати якоюсь визначеною загальною формою, то не може бути запропоновано будь-якого аналітичного прямого методу для розв’язання такої системи. З наближених ітераційних методів найбільш простим є метод простої ітерації, що базується на приведенні системи (3.10) до системи нелінійних рівнянь у вигляді:

.

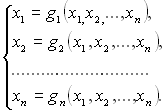В матричному вигляді

,

де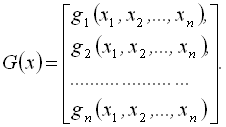

Далі може бути застосований алгоритм, аналогічний методу Гаусса-Зейделя для систем лінійних рівнянь. В його основі ітераційні рівняння, що пов’язують та m ітерації

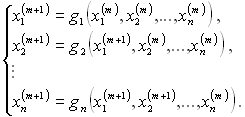
Для цього методу дуже важко забезпечити збіжність, а інтервал збіжності може бути настільки вузьким, що вибір початкових наближень сильно ускладнюється.

В загальному випадку цей метод буде збігатися, якщо де – норма матриці частинних похідних функцій по змінних

.

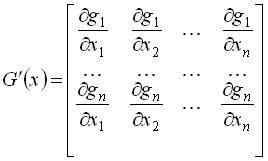Для розв’язання систем нелінійних рівнянь широке застосування набув більш стійкий метод – метод Ньютона. Він є аналогом методу Ньютона для одного рівняння і базується на розкладанні всіх n рівнянь у ряд Тейлора:

……………………………………………………………………….

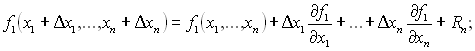
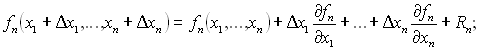
де R_n – члени другого та більших порядків, що в подальшому відкидаються.

Задача зводиться до розв’язання системи лінійних рівнянь

.

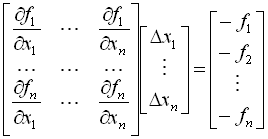В цій системі матрицю частинних похідних називають матрицею Якобі і позначають W(X).

Знайдені для певного (m+1) кроку ітерації значення використовуються як поправки до попередніх наближень

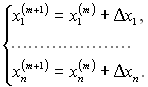
Загальна ітераційна формула в матричному поданні має вигляд:

,

де – вектор-стовпець значень функцій для наближень – обернена матриця Якобі.

Алгоритм методу Ньютона подано на рисунку 3.9.

Певні труднощі при реалізації алгоритму методу Ньютона виникають при оберненні матриці Якобі. Для цього використовуються відомі з лінійної алгебри способи обернення матриць.

Існує багато варіантів застосування методу Ньютона. Наприклад, модифікований метод Ньютона

.

В цьому методі не треба обчислювати обернену матрицю Якобі на кожному кроці розрахунків, що спрощує алгоритм, але уповільнює збіжність і робить метод більш чутливим до вибору початкового наближення.

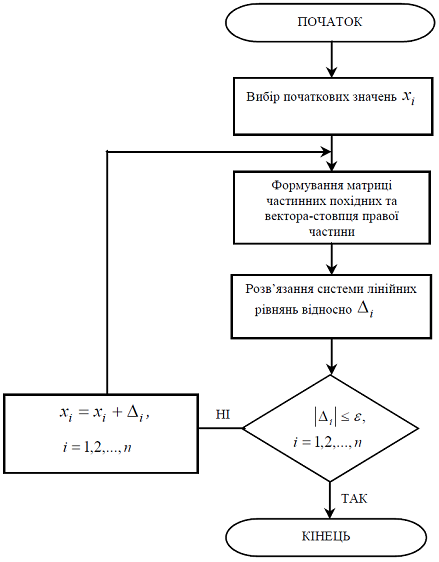
Рисунок 3.9 – Алгоритм методу Ньютона для систем нелінійних рівнянь

 

Метод Ньютона з параметром

Цей метод дещо схожий з методом послідовної верхньої релаксації для систем лінійних рівнянь.

Застосовуються також різноманітні гібридні методи, в яких поєднується метод Ньютона з методом простої ітерації.

Збіжність методу Ньютона оцінюється шляхом обчислення показника

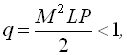
де

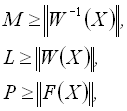
причому

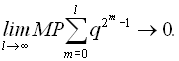
Похибка на m-ій ітерації визначається нерівністю

 

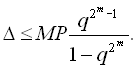
Контрольні запитання та завдання

1. Навести класифікацію нелінійних рівнянь і систем та методів їх розв’язання. В яких задачах з автоматики та систем управління виникає потреба розв’язання таких задач?

2. Сформулювати головні теореми та правила відносно кількості та виду коренів алгебраїчних рівнянь.

3. Розв’язати алгебраїчне рівняння з комплексними коренями

Похибка оцінки кожного кореня не повинна перевищувати 0.05.

4. Чому для розв’язання систем нелінійних рівнянь можливо застосування тільки ітераційних методів?

5. Назвати ітераційні методи для розв’язання систем нелінійних рівнянь та порівняти їх.

6. Як оцінюється збіжність ітераційних методів розв’язання систем нелінійних рівнянь.

7. Скласти алгоритм і програму та розв’язати на ЕОМ методами половинного ділення, хорд, Ньютона, січних та простої ітерації (оцінити інтервал збіжності) з похибками = 0.1,0.01,0.001 такі рівняння:

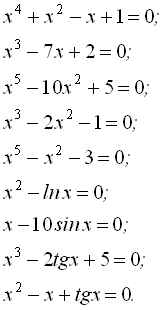
Порівняти ефективність (час розрахунків та кількість ітерацій для досягнення заданої похибки) різних методів.

8. Знайти матриці Якобі для систем нелінійних рівнянь:

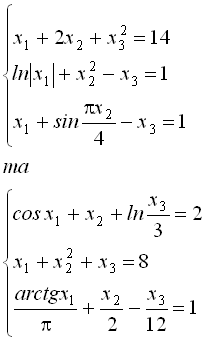
9. Як знайти матрицю обернену заданій? Скласти алгоритм.

10. Розв’язати на ЕОМ системи рівнянь з п. 8 методом Ньютона та модифікованим методом Ньютона. Скласти алгоритм та програму. Оцінити збіжність.

11. Дати порівняльну оцінку та рекомендації щодо вибору методів розв’язання нелінійних рівнянь та систем.