Розділ 4 Методи розв’язання диференціальних рівнянь

 

Переважна більшість об’єктів є нестаціонарними, вони змінюються у часі під впливом внутрішніх та зовнішніх чинників. Для формального опису нестаціонарних процесів був розроблений спеціальний математичний апарат, який отримав назву диференціальних рівнянь.

Диференціальними рівняннями (Differential equations) називаються такі рівняння, які крім невідомих функцій однієї або декількох незалежних змінних, містять також і їхні похідні. Диференціальні рівняння (ДУ) називають звичайними (ЗДУ), якщо невідомі функції є функціями однієї змінної, в іншому випадку ДУ називатися рівняннями в частинних похідних.

Співвідношення

,                    (4.1)

що поєднує змінну х, невідому функцію Y = Y(x) і її похідні до порядку (n) включно, називають ОДУ n- го порядку.

Рівняння (4.1) часто представляють у так званому канонічному вигляді:

          y(n)(х)=f (x, y(х), y(1)(х), y(2)(х),…, y(n-1)(х)).    

ЗДР має нескінченну множину розв’язків, оскільки функція y(х), що є розв’язком рівняння n-го порядку, містить n невідомих констант, які виникають під час інтегрування. Для пошуку якого-небудь конкретного розв’язку потрібні додаткові умови, які дозволять знайти значення констант. Ці умови можуть бути різними і приводити до різних задач. У випадку, коли додаткові умови задаються при одному значенні незалежної змінної, має місце задача Коші (задача з початковими умовами). Якщо умови задаються для двох або більше значень незалежної змінної, то задача стає крайовою. У задачі Коші додаткові умови називаються початковими, а у крайовій задачі – граничними. Наприклад, для диференціального рівняння n-го порядку початкові умови мають вигляд:

,

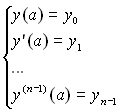де а – початок відрізку, на якому вирішується задача; y0, y1, … ,yn-1 – деякі числа.

Для практичної реалізації із загального запису ДР (4.1) намагаються виразити старшу похідну, так для n = 1 співвідношення (4.1) прийме вигляд:

Y' = f(x, Y);

Y" = f(x, Y, Y' ), якщо n = 2.

Дамо геометричну інтерпретацію ДР першого порядку. Його рішення можна зобразити у вигляді сімейства кривих на площині X0Y :

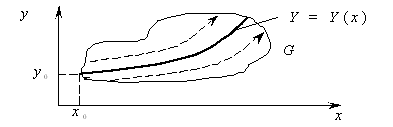
Рисунок 4.1 – Геометрична інтерпретація ДР

 

Нехай неявна функція f(x,y) визначена та неперервна в області G цієї площини. У кожній точці площини G функція f(x,y) задає деякий напрямок. У цілому це буде поле напрямків. Для загального рішення потрібно знайти всі інтегральні криві, дотичні до яких у кожній точці збігаються з напрямком поля. А рішення Y = Y(x) є частковим рішенням, що відповідає певній константі. Через кожну точку з області рішення проходить одна інтегральна крива. Для ДР при n > 1 через кожну точку проходить не одна інтегральна крива і потрібно n додаткових умов, тобто для рівнянь вищих порядків геометрична інтерпретація їхніх рішень більше складна. А знайти загальне рішення в аналітичному виді вдається навіть для ДУ першого порядку тільки в деяких випадках. Частковий розв’язок теж доводитися шукати наближено.

Методи рішення ЗДР можна розбити на наступні групи: графічні; аналітичні; наближені аналітичні; чисельні.

Задачу Коші можна сформулювати таким чином.

Нехай дано диференціальне рівняння першого порядку

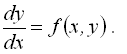          (4.2)

Потрібно знайти функцію на відрізку від х = а до х=b, що задовольняє як рівняння (4.1), так і початкову умову (при цьому завжди припускається, що існує єдиний розв’язок на всьому відрізку).

Задача, що полягає в розв’язанні звичайного диференціального рівняння при додаткових умовах, які поставлені при декількох значеннях незалежної змінної, називається крайовою.

Крайову задачу розглянемо на прикладі звичайного диференціального рівняння другого порядку:

при граничних умовах y (a) = A, y (b) = B.

Постановки і методи розв’язання рівнянь більш високих порядків аналогічні.

Для розв’язання диференціальних рівнянь можливо використовувати аналітичні і чисельні методи. Аналітичні методи дозволяють знайти розв’язок невеликої кількості типів рівнянь, тому їх застосування є вельми обмеженим. Чисельні методи дозволяють вирішувати значно більшу кількість задач. В основі застосування чисельних методів лежить дискретизація відрізку [a,b] з кроком h, в результаті чого формується послідовність вузлів xk=а+hЧk, , . Питома функція y(х) знаходиться у вигляді таблично-заданої функції, значення якої розраховуються в виділених вузлах.

 

4.1 Методи розв’язання задачі Коші

 

Основою чисельних методів розв’язання диференціальних рівнянь слугує розкладання функції y в ряд Тейлора в околі початкової точки

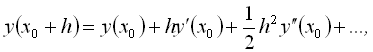
де – відстань (крок) між початковою точкою x0 і точкою x1=x0 + h, в якій відшукується розв’язок.

В різних методах враховується різна кількість членів розкладання ( в багатокрокових методах в поєднанні з інтерполяційними формулами), що визначає точність обчислень. При використанні цих методів на ЕОМ слід розрізняти похибки округлення через обмеженість кількості значущих цифр в ЕОМ; похибка зрізання (обмеження) - методична похибка, що пов’язана з апроксимацією розв’язків скінченими рядами, замість нескінченних, наприклад, рядами Тейлора.

Внаслідок цих причин виникають два види похибок:

  •  локальна – сума похибок, що вносяться в обчислювальний процес на конкретному кроці;
  •  глобальна (сумарна) – різниця між точним і обчисленим значеннями, яка включає так звану похибку розповсюдження внаслідок накопичення помилок на попередніх етапах обчислення.

    Порядок методу дорівнює р, якщо існує таке позитивне число , що

    де – локальна помилка; h – крок дискретизації.

    Число с не залежить від номеру кроку і його величини, а визначається похідними і довжиною інтервалу. При апроксимації розв’язання рядами Тейлора воно зв’язане зі степенем членів ряду, які відкидаються.

    Методи розв’язання задачі Коші поділяють на однокрокові та багатокрокові.

    В однокрокових методах для знаходження наступної точки на кривій

    y = f(x) потрібна інформація лише про один попередній крок (методи Ейлера і Рунге – Кутта).

    В багатокрокових методах (прогнозу і корекції) для знаходження наступної точки на кривій y =f(x) потрібна інформація більш ніж про одну з попередніх точок. Щоб отримати достатньо точне чисельне значення часто використовується ітераційна процедура (наприклад, в методах Мілна – Адамса, Башфорта, Хеммінга).