7.3 Дискретні та неперервні сигнали.

 

Більшість реальних сигналів (наприклад, звукових) є неперервними функціями. Для цифрової обробки таких сигналів їх потрібно перевести в цифрову форму. Один зі способів зробити це – рівномірно по часу виміряти значення сигналу на певному проміжку часу і ввести отримані значення амплітуд. Якщо робити вимірювання досить часто, то за значеннями отриманого дискретного сигналу можна буде досить точно відновити вигляд вихідного неперервного сигналу.

Дискретні сигнали (discrete signal) утворюють шляхом множення аналогового сигналу x(t) на так звану функцію дискретизації y(t), яка представляє собою періодичну послідовність коротких імпульсів, що слідують з кроком дискретизації (рис. 7.4а).В ідеальному випадку в якості функції дискретизації використовується періодична послідовність дельта-функцій (рис. 1.4б).

Процес вимірювання величини сигналу через рівні проміжки часу називається рівномірною (за часом) дискретизацією. Багато пристроїв для введення даних здійснюють дискретизацію.

Рисунок 1.3 – Дискретизований сигнал

 

Наприклад, звукова карта дискретизує сигнал з мікрофона, сканер дискретизує сигнал, що поступає з фотоелемента. У результаті дискретизації безперервний (аналоговий) сигнал перетворюється у послідовність значень. Пристрій, що виконує цей процес, називається аналогово-цифровим перетворювачем (АЦП, analogue-to-digital converter, ADC). Частота, з якою АЦП здійснює вимірювання значень аналогового сигналу і видає його цифрові значення, називається частотою дискретизації.

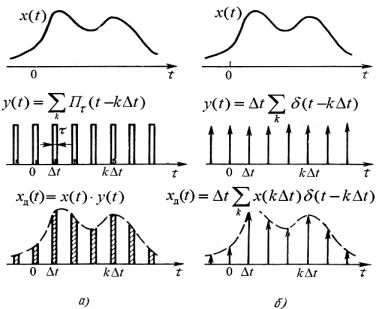
Рисунок 1.4 – Д искретизація сигналу

 

Інтервал називають періодом дискретизації, частотою дискретизації є оберненою величиною

Значення послідовності в моменти часу nT називають відліками. Дискретний сигнал може бути як дійсним так і комплексним. В останньому випадку його дійсна та уявна частини описуються дійсними послідовностями

Математично дискретний сигнал визначають:

  •  функцією дискретного часу : , що

    відповідає вибіркам аналогового сигналу в дискретні періодично повторювані моменти часу;

  •  функцією номера вибірки :, що в загальному випадку не пов’язана з часом;
  •  функцією неперервного часу :

    що отримують множенням аналогового сигналу x(t) на дискретизуючу функцію у вигляді періодичної послідовності 8 імпульсів з періодом, що є рівним:

    Графічно дискретні сигнали представляються функцією номера вибірки n або дискретного часу (рис. 1.5).

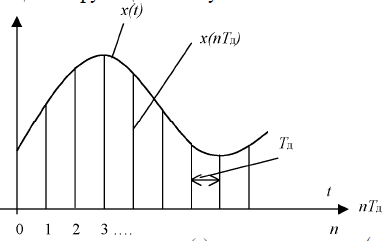
    Рисунок 1.5 – Графік неперервного та дискретного сигналу

     

    7.4 Теорема Котельникова.

     

    Для того, щоб відновити вихідний безперервний сигнал з дискретизованого з малими похибками, необхідно раціонально вибрати крок дискретизації. Тому при перетворенні аналогового сигналу в дискретний обов'язково виникає питання про величину кроку дискретизації. Якщо аналоговий сигнал має низькочастотний спектр, обмежений деякою верхньою частотою (тобто функція u(t) має вигляд кривої, яка плавно змінюється, без різких змін амплітуди), то навряд чи на деякому невеликому часовому інтервалі дискретизації ця функція може істотно змінюватися по амплітуді.

    Очевидно, що точність відновлення аналогового сигналу по послідовності його відліків залежить від величини інтервалу дискретизації. Чим він коротше, тим менше буде відрізнятися функція u(t) від плавної кривої, що проходить через точки відліків. Однак зі зменшенням інтервалу дискретизації, істотно зростає складність і обсяг обчислень. При досить великому інтервалі дискретизації зростає ймовірність спотворення або втрати інформації при відновленні аналогового сигналу.

    Оптимальна величина інтервалу дискретизації встановлюється теоремою Котельникова, яка має важливе теоретичне та практичне значення: дає можливість правильно здійснити дискретизацію аналогового сигналу та визначає оптимальний спосіб його відновлення на приймальному кінці за відліковим значенням.

    Відповідно до однієї з найбільш відомих і простих інтерпретацій теореми Котельникова, довільний сигнал s(t), спектр якого обмежений деякою частотою може бути повністю відновлений по послідовності своїх відлікових значень, що слідують з інтервалом часу

    Інтервал дискретизації та частоту часто називають відповідно інтервалом і частотою Найквіста. Аналітично теорема Котельникова представляється рядом

    де k – номер відліку; – значення сигналу в точках відліку.

    Фізичний зміст цієї теореми стає зрозумілим, якщо розглянути спектри сигналів і .

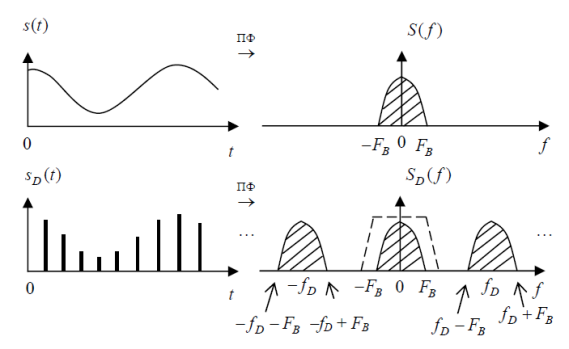
    Рисунок 1.6 – Теорема Котельникова

     

    З рис. 1.6 видно, що містить у собі і ще нескінченне число копій , зсунутих одна відносно одної на частоту дискретизації . Якщо пропустити сигнал через фільтр нижніх частот (ФНЧ), амплітудно-частотна характеристика якого показана на цьому ж рисунку, на виході ФНЧ залишиться тільки , тобто відновиться вихідний сигнал s(t) .

    При копії не перетинаються з основним пелюстком спектра і таке відновлення можливе.

    При копії стикаються з основним пелюстком, однак виділення вихідного сигналу s(t) ще можливе за допомогою ідеального ФНЧ із нескінченною крутизною спаду амплітудно-частотної характеристики (АЧХ).

    При пелюстки спектра перекриваються і відновлення вихідного сигналу s(t) неможливим.

    На практиці частоту завжди вибирають більшою, ніж , тому що будь-який фільтр має далеко не нескінченну крутизну спаду АЧХ.

    Спектр реального сигналу рідко має точну верхню границю. Найчастіше зменшується з ростом частоти, асимптотично наближуючись до нуля. У такому випадку на вході дискретизуючого пристрою поміщають ФНЧ, що має частоту, рівну ефективній ширині спектра вихідного аналогового сигналу. Його призначення – забрати залишки спектра за межами і тим самим виключити перекриття пелюстків спектра .

    На практиці ця теорема має величезне значення. Наприклад, відомо, що більшість звукових сигналів можна з деякою мірою точності вважати сигналами з обмеженим спектром. Їх спектр, в основному, лежить нижче 20 кГц. Це означає, що при дискретизації з частотою не менш 40 кГц, ми можемо достатньо точно відновити вихідний аналоговий звуковий сигнал по його цифровим відлікам. Абсолютної точності досягти не вдасться, тому що в природі не буває сигналів з ідеально обмеженим спектром.

    Пристрій, який інтерполює дискретний сигнал до безперервного, називається цифро-аналоговим перетворювачем (ЦАП, digital-to-analogue converter). Ці пристрої застосовуються, наприклад, в програвачах компакт-дисків для відтворення звуку з цифрового звукового сигналу, записаного на компакт-диск. Частота дискретизації звукового сигналу під час запису на компакт-диск становить 44100 Гц. Таким чином, і ЦАП на CD-плеєрі працює на частоті 44100 Гц.