До статистичних методів можна віднести кореляційний аналіз зображень. На основі кореляційного підходу найбільш успішним є метод матриць взаємозв’язку (co-occurrence matrices – GLCM). Дані матриці характеризують частоту пар різних градацій сірого кольору, що присутні в зображенні, і визначаються шляхом кореляційного аналізу пікселів зображення, при цьому якщо піксель відповідає вибраній градації, то він враховується як одиничне значення, якщо ні, то як нульове. У випадку кольорових зображень даний підхід використовують до аналізу кожного з трьох базових кольорів. Як слідує з методу формування матриць взаємозв’язку, вони найкраще підходять до розв’язання задач класифікації текстур.

Наряду з статистичним аналізом в просторовій області використовують аналогічний аналіз в спектральній області із застосуванням двохвимірного дискретного перетворення Фур’є в базисі різних ортогональних функцій – дискретних експоненціальних функцій (ДЕФ), косинусних, Уолша-Адамара, Хаара та інших. Для аналізу текстур використовують метод гістограм розподілу спектральних коефіцієнтів. Загальною характеристикою такого підходу є те, що гістограми спектральних коефіцієнтів, що отримані в результаті інтегральних перетворень, більш стійкі та надійні ніж гістограми розподілу окремих пікселів чи груп пікселів. Даний метод також не чутливий до присутнього в зображенні шуму, але це є одночасно і недоліком в разі використання методу до розв’язання задачі розпізнавання незначних за розміром об’єктів на текстурованому фоні. Також спектральні методи згладжують різкі границі між об’єктами зображення.

Статистичний аналіз пікселів та спектральних коефіцієнтів на основі гістограм в основному використовують до класифікації статичних текстур, до аналізу динамічних текстур використовують методи на основі кореляційного аналізу.

Найпростішою і найбільш часто вживаною є стохастична модель . Фон зображення характеризують гістограмою розподілу значень кольору по величині в деякій базовій області, вільній від об’єктів. Гістограму апроксимують функцією щільності розподілу ймовірності, найбільш часто гаусовою. В цьому випадку параметрами моделі є середнє значення та дисперсія . За максимальне відхилення сигналу моделі приймають . В якості мінімального порогового значення величини відхилення можна прийняти величину .

В якості прикладу розглянемо алгоритм розпізнавання зображення об’єктів за допомогою стохастичної моделі:

               (2.11)

де , – елементи матриць заданого зображення та зображення об’єктів. На рис. 2.2 представлено результат розпізнавання та відбору об’єктів згідно з алгоритмом (2.11) за статистичним методом.

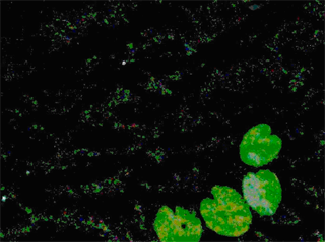
Рисунок 2.2 – Тестове зображення та результат розпізнавання об’єктів за статичним методом

Метод побудови моделі та її застосування наступний:

1. Фрагмент зображення фону, вільний від сторонніх предметів, розміром пікселів використано як базовий для того, щоб знайти статистичні параметри фону.

2. За допомогою виразу (2.11) створено зображення об’єктів.

Як видно з рисунку, всі сторонні об’єкти, як великі (листки), так і малі (білого кольору) виділені, але присутній шум похибки. Зменшити похибку можна збільшивши порогове значення відбору, але, як показали чисельні експерименти, в цьому випадку втрачають якість зображення об’єктів. Таким чином, стохастична модель погано апроксимує фоновий сигнал та не спроможна повністю відділити шукані об’єкти від фону.