8.1.4 Методи на основі динамічних моделей

 

Для аналізу зображень використовують двохвимірні дискретні лінійні та нелінійні моделі, що описують динаміку поверхні зображення у просторі . В найбільш загальній формі лінійну модель описують системою рівнянь виду

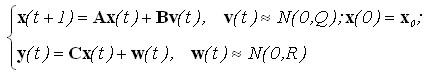          (2.24)

де – вектор зображення, – вектор стану динамічної моделі, – матриця-оператор моделі має наступну структуру,

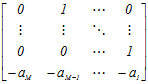                         (2.25)

– порядок моделі, – параметри оператора моделі, – матриця фільтра ковзного середнього, – матриця функціонального перетворення при вимірюванні значень елементів зображення, , – вектори гаусового центрованого шуму з кореляційними функціями та , – вектор початкових або граничних значень. Систему рівнянь широко використовують в системах керування. Методи на основі рівняння стану (1.24) допускають, що можуть існувати численні динамічні текстури в різних областях зображення. Їх визначають як локальні, що відповідають невеликим просторовим регіонам. Локальні текстури мають різні динамічні властивості, що задані відповідними рівняннями стану. На рис.2.6 наведено приклад зображення, що поділено на блоки. Кожний окремий блок має власну динамічну модель. На рис.2.7 представлено три типи імпульсних характеристик локальних моделей.

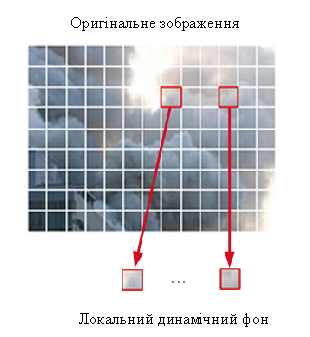
Рисунок 2.6 – Приклад локального динамічного фону.

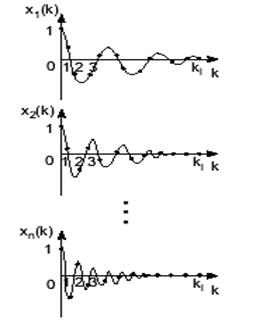
Рисунок 2.7 – Імпульсні характеристики змінних стану.

    

Для моделювання текстур використовують модель (2.24) із спрощеною характеристикою векторів шуму, допускаючи, що відліки шуму не корелюють, тоді , де – дисперсія гаусового шуму, – дельта функція. В цьому випадку модель (2.24) можна представити як авторегресію із ковзним середнім (AutoRegression and Moving Average – ARMA), дана модель має наступний вигляд.

     ,                (2.26)

де – відліки сигналу зображення, – коефіцієнти лінійного передбачення (ЛП), – відліки білого шуму, – параметри, що задають порядок моделі умовно по координатам , – коефіцієнти та порядок складової ковзного середнього. Модель (2.26) включає дві складові – модель авторегресії (AR) (autoregression – AR), що описує динамічні властивості сигналу зображення, та модель ковзного середнього (moving average – МА), що описує властивості сигналу похибки. Для розв’язання задач розпізнавання та класифікації використовую саме авторегресійну складову, модель МА похибки використовують як допоміжну, що характеризує якість моделі AR. Тому більш широке застосування в обробці зображень знайшла модель AR

     ,                     (2.27)

де – відліки похибки з дисперсією . Параметри моделі (2.27) – коефіцієнти ЛП, можна знайти за допомогою методу найменших квадратів. Одною із найбільш важливих задач при синтезі моделі AR є вибір її порядку таким чином, щоб модель була адекватна даним, і разом з тим, не була чутливою до незначних флуктуацій. Критерієм адекватності моделі може служити співвідношення потужності сигналу зображення до величини похибки (шуму). В літературі це визначають терміном Signal to Noise Ratio (SNR):

                         (2.28)

де – потужність сигналу базового фрагмента зображення, що використано для визначення параметрів моделі, – дисперсія шуму похибки. Не чутливість моделі до незначних флуктуацій зображення досягають за допомогою умови інваріантності параметрів моделі до зсуву базового фрагмента відносно координат, в яких задано зображення. Це також важлива властивість моделі і їй приділяють особливу увагу в літературі по обробці зображень. Вона стосується всіх перелічених вище моделей. Для того, щоб модель була інваріантною до зсуву координат і разом з тим була адекватною даним, вона повинна виконувати функції апроксимації та екстраполяції даних сигналу зображення.

У випадках, коли модель AR не адекватна динаміці даних, використовують дискретну нелінійну модель у вигляді ряду Вольтера. Постільки така модель в разі двохвимірних даних потребує значного числа параметрів, то на практиці застосування найшли моделі не вище третього порядку нелінійності. Нелінійну модель другого порядку можна представити як

(2.29)

де – коефіцієнти та порядок нелінійної складової. Визначити параметри моделі (2.29) можна за допомогою розширеної системи рівнянь, що включає квадратичні складові сигналу. Розв’язати таку систему рівнянь можна за допомогою методу найменших квадратів. Тому нелінійна модель простіша ніж модель ARMA.

Алгоритм обробки зображення за допомогою моделей наступний:

     1) за допомогою базового фрагмента зображення визначають параметри моделі та параметри, що характеризують якість моделі (наприклад, статистичні параметри шуму похибки);

     2) сигнал зображення обробляють за допомогою моделі і визначають параметри якості;

     3) якщо параметри якості відповідають параметрам базового фрагмента, то зображення розпізнано, якщо ні, то зображення не розпізнано.