8.1.7 Методи визначення контурів елементів зображень та сегментації
Для визначення контурів зображень використовують статистичний аналіз фрагментів зображення та їх взаємну кореляцію з метою знаходження стрибкоподібних змін кольору і освітленості. Велика група методів заснована на використанні математичних моделей, що відображають певну взаємодію між окремими пікселями або фрагментами зображень. Також для розв’язання задач розпізнавання об’єктів застосовують різні методи фільтрації, наприклад інверсні фільтри, фільтри Вінера, Байєса. При цьому використовують аналогію між динамікою зображень та фізичними процесами, наприклад дифузії. Для розв’язання деяких задач використовують стохастичні моделі.
Ряд методів визначення контурів зображень реалізовано в середовищі Matlab. У випадку динамічного фону дані методи не дозволяють отримати інформативний результат, так як перетворюють зображення в безліч контурних об’єктів. В цьому можна переконатись здійснивши розпізнавання контурів зображення за допомогою функції edge, вибравши один з запропонованих фільтрів Собеля, Превіта, Робертса, лапласіан-гаусіана або за методом Канні.
Розпізнавання об’єктів за допомогою визначення контурів виконується функцією edge. Найкращий результат отримано за методом Канні, що представлено на рис. 2.8. Суть методу полягає в пошуку локальних ділянок з перепадами яскравості. Перепади яскравості шукають за допомогою фільтрації по кожній з осей координат одномірним фільтром лапласіан-гаусіана. У методі Канні для класифікації перепадів на "слабкі" і "сильні" використовується два пороги – нижній і верхній. "Слабкі" границі відзначаються в результуючому зображенні, тільки якщо вони з'єднані з "сильними". Для зображень, що зіпсовані шумом, даний метод забезпечує найкраще виявлення границь у порівнянні з іншими методами функції edge та методом сегментації, але вимагає істотно більшого часу.
Алгоритми сегментації зображень базуються на одній з двох характеристик сигналу яскравості – розривності або однорідності. В першому випадку підхід базується на розбитті зображення на основі різких змін сигналу, таких як перепади яскравості на зображенні. Зазвичай пошук розривів здійснюється за допомогою ковзних масок. Друга категорія методів базується на визначенні однорідності зображення згідно наперед обраних критеріїв. Прикладами таких методів є порогова обробка, злиття та розбиття областей. За допомогою Mathlab сегментацію можна виконати застосовуючи функцію qtdecomp за методом розподілу. Суть методу полягає в наступному. Зображення розбивається на блоки, що не перекриваються. Кожний блок за допомогою деякого критерію перевіряється на однорідність. Якщо блок неоднорідний, то він розбивається на блоки меншого розміру. Процес завершується тоді, коли жодний з блоків не може бути розділений.

Рисунок 2.8 – Розпізнавання об’єктів за допомогою функції edge.
8.2. Фрактальні методи
У той час як об'єкти, побудовані людиною, такі як промислові та житлові будинки, можуть бути ефективно описані набором простих геометричних примітивів: кубів, сфер, циліндрів, конусів, кольорові текстури природного походження, через свою нерегулярність і фрагментарність, погано піддаються такому опису..У зв'язку із цим, для аналізу таких текстур виявляється природним подання їх у вигляді фрактала з деяким розміром D.
Фрактал (лат. fractus, fractal – дроблений) – термін, який ввів Бенуа Мандельброт в 1975 році для позначення нерегулярних самоподібних множин.
Фрактал – це нескінченно самоподібна геометрична фігура, кожний фрагмент якої повторюється при зменшенні масштабу. Масштабна інваріантність, що спостерігається у фракталах, може бути або точною, або наближеною.
Ще один варіант визначення: фрактал – самоподібна множина нецілої розмірності. Самоподібна множина – множина, що представляється у вигляді об'єднання однакових непересічних підмножин подібних до вихідної множини.
Основні властивості фракталів:
У наш час фрактали знайшли своє застосування при аналізі текстур ландшафтів, отриманих при аерокосмічній зйомці, при аналізі поверхонь порошків та інших пористих середовищ, при аналізі поверхні хмар тощо. Однак розмір фрактала кольорової текстури багато в чому залежить від вибору методу оцінки. Так, при використанні різних методів оцінки розміру фрактала, ми одержимо відповідно й різні його розміри. Зіставлення текстур, таким чином, можливо при використанні того самого методу (групи методів). Більше того, не всі текстури добре розрізняються по розміру фрактала. У зв'язку із цим перш, ніж включати в систему ознак розмір фрактала, необхідно оцінити фрактальність текстури. Оцінка фрактальності текстури здійснюється на основі обраного методу оцінки розміру фрактала. Оскільки розмір фрактала обчислюється через оцінку вибіркової регресії, то природно оцінювати фрактальність текстури за коефіцієнтом кореляції між логарифмом випадкової величини й логарифмом заданої функції кроку. При цьому ухвалення рішення про фрактальність текстури можна будувати таким чином:
1. побудувати залежність коефіцієнта кореляції від кроку; значення кроку, при якому функція має максимум, є максимальним кроком у діапазоні кроків, що задаються, при оцінці розміру фрактала;
2. не враховувати оцінку розміру фрактала при низькому коефіцієнті кореляції в тих методах, де використовується оцінка фрактала як середнє значення в серії експериментів;
3. не включати розмір фрактала в систему ознак для сегментації текстур при значеннях коефіцієнта кореляції < 0,7 .
Оцінка фрактальності текстури є важливою характеристикою при сегментації по розмірі фрактала.
Поширення фрактального опису пояснюється тим, що більшість просторових систем у природі є нерегулярним і фрагментарним, форма цих систем погано піддається опису апаратом евклідової геометрії. Наприклад, берегова лінія острова не пряма й не кругла, і ніяка інша класична крива не може служити для опису й пояснення її форми без надмірної штучності й ускладнення.
Фрактальні структури є одним із різновидів текстур, де деталізація зображення досягається представленням об’єкта подібними меншої величини. Деякі динамічні текстури, наприклад поверхні лісу і хвиль води, хмари, пористі мінерали, метало-структури, можуть бути представлені за допомогою фрактальної екстраполяції. Суть фрактальних методів в задачах розпізнавання об’єктів полягає в наступному. Обриси штучних об’єктів – танків, автомобілів, створюються лініями, що описуються рівняннями цілого порядку. Природні об’єкти – рельєф, дерева, фрактальні, тобто мають фрактальну розмірність. Використовуючи цю властивість за допомогою фрактальної апроксимації об’єктів зображення можна створити систему розпізнавання образів. Така система не бачить кущ, але добре розпізнає штучний об’єкт, схований за кущем. Основною перевагою даного методу над іншими є те, що він не чутливий до перешкод. На результат розпізнавання не впливає колір та контрастність об’єкта по відношенню до фону, впливає лише площа, яку займає шуканий об’єкт на зображенні. В цьому полягає недолік даного методу – за допомогою фрактального аналізу можна розпізнавати об’єкти, що за розміром порівняні зі структурою елементів фону.
Класифікації фракталів. В основному фрактали ділять на геометричні (рис.2.9), алгебраїчні й стохастичні. Однак існують і інші класифікації: рукотворні й природні. До рукотворних належать ті фрактали, які були винайдені вченими, вони при будь-якому масштабі володіють фрактальными властивостями. На природні фрактали накладається обмеження на область існування – тобто максимальний і мінімальний розмір, при яких у об'єкта спостерігаються фрактальні властивості.
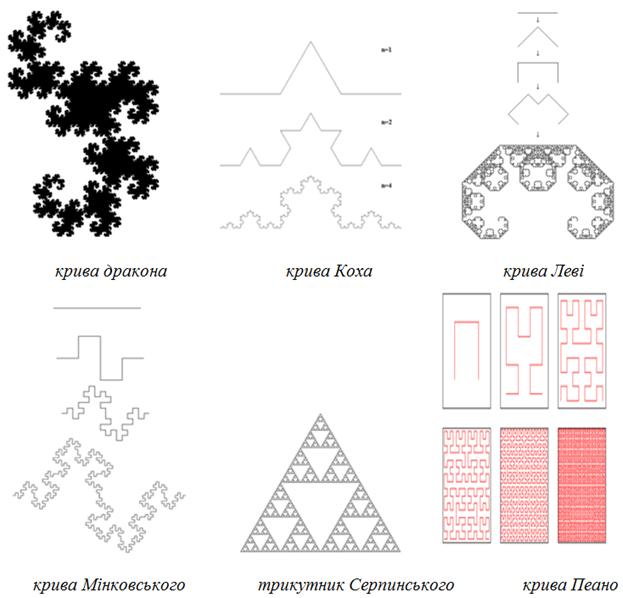
Рисунок 2.9 – Приклади геометричних фракталів
Для побудови алгебраїчних фракталів (рис.2.10) використовуються ітерації нелінійних відображень, що задаються простими алгебраїчними формулами. Найбільш вивчений двомірний випадок. Нелінійні динамічні системи можуть володіти декількома стійкими станами. Кожний стійкий стан (атрактор) має деяку область початкових станів, при яких система обов'язково в нього перейде. Таким чином, фазовий простір розбивається на області притягання атракторів.

Рисунок 2.10 – Приклад алгебраїчного фракталу. Множина Жюліа́
Якщо фазовим є двомірний простір, то, зафарбовуючи області притягання різними кольорами, можна одержати кольоровий фазовий портрет цієї системи (ітераційного процесу). Міняючи алгоритм вибору кольору, можна одержати складні фрактальні картини з вигадливими багатобарвними візерунками. Несподіванкою для математиків стала можливість за допомогою примітивних алгоритмів породжувати дуже складні нетривіальні структури. Приклади алгебраїчних фракталів: множина Мандельброта, множина Жюліа, басейни Ньютона, біоморфи.
Геометричні фрактали застосовуються для одержання зображень дерев, кущів, берегових ліній тощо. Алгебраїчні та стохастичні – при побудові ландшафтів, поверхні морів, моделей біологічних об'єктів та інше.
З математичної точки зору, фрактал – це передусім множина з дробовою розмірністю (fractional dimension). Ми добре уявляємо собі, що точка має розмірність 0, коло та відрізок – розмірність 1, куб та сфера – 2. З одномірними об’єктами ми пов’язуємо поняття довжини, з двухмірними – площі і т.д. Але як можна уявити собі множину з розмірністю 3/2? Для цього необхідно дещо проміжне між довжиною та площиною, і якщо довжину умовно назвати 1-мірою, а площу – 2-мірою, то необхідна (3/2)-міра. Хаусдорф визначив таку α-міру для будь-якого α≥0 і на цій основі кожній множині в евклідовому просторі надав у відповідність число. Для пояснення фрактальної розмірності необхідно ввести поняття топологічної розмірності. Під топологічною розмірністю множини в лінійному просторі розуміють число лінійно незалежних координат в просторі. Фрактальна розмірність множини – розмірність того простору, яке повністю заповнюється множиною. Для зв’язку фрактальної та топологічної розмірності використовують показник Херста Н, який обчислюється за формулою H = D - Dt. Ідеї Хаусдорфа були розвинуті А.С.Безіковичем. В наступні роки розмірність Хаусдорфа-Безіковича отримала застосування в деяких розділах математики, але нічого не передбачувало їй тієї популярності цього поняття за межами математики, яка спостерігається тепер. Частково цьому допомогла наукова діяльність Б.Мандельброта, який в своїх книгах привів яскраві приклади застосування фракталів для пояснення деяких природних явищ. Тобто, фрактальна розмірність, як правило, є невід’ємним нецілим числом, яке показує деяким чином геометричну складність об’єкту.
Розмірність фрактала ![]() визначається як
визначається як
![]() (2.30)
(2.30)
де ![]() – співвідношення подібності,
– співвідношення подібності, ![]() – число кроків, необхідне для того, щоб покрити криву.
– число кроків, необхідне для того, щоб покрити криву.
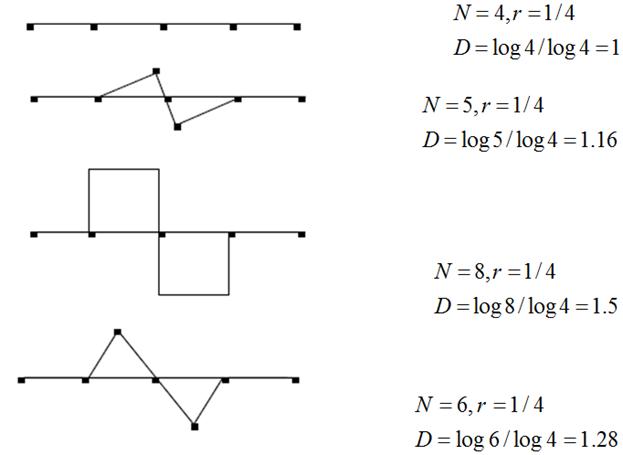
Рисунок 2.11 – Визначення розміру фрактала на прикладі чотирьох ламаних ліній.
Практично розмір фрактала для кривої оцінюється шляхом вимірювання довжин кривої при різних розмірах кроку. Розмірність фрактала D може бути оцінена за допомогою наступного рівняння регресії:
![]() (2.31)
(2.31)
де L – довжина кривої, B – нахил регресії, G – величина кроку, С – константа.
Розглянемо докладніше реалізацію фрактального підходу до аналізу хмар. В основу цього методу покладене виведене Мандельбротом співвідношення між периметром і площею об'єкта. Для окружностей, квадратів, рівносторонніх трикутників та інших багатокутників відношення периметра до квадратного кореня із площі, що ним обмежується не залежить від розміру фігури і є постійною величиною для даного сімейства. Аналогічно для сімейства подібних островів відношення довжини нефрактальної берегової лінії будь-якого острова до квадратного кореня з його площі не залежить від розміру площі. Однак, якщо берегова лінія фрактальна, то її довжина ![]() залежить від довжини еталона
залежить від довжини еталона ![]() і прямує до безкінечності якщо еталон також прямує до нуля.
і прямує до безкінечності якщо еталон також прямує до нуля.
При цьому площа острова ![]() , обумовлена кількістю квадратів
, обумовлена кількістю квадратів ![]() , що на ній розташовані, залишається кінцевої. Таким чином, відношення периметра до квадратного кореня із площі розходяться. Мандельброт для випадку фрактальной берегової лінії одержав наступне співвідношення між периметром і площею:
, що на ній розташовані, залишається кінцевої. Таким чином, відношення периметра до квадратного кореня із площі розходяться. Мандельброт для випадку фрактальной берегової лінії одержав наступне співвідношення між периметром і площею:
![]() (2.32)
(2.32)
Це співвідношення виконується для будь-якого еталона довжини ![]() , досить малого, щоб задовільно виміряти найменший з островів.
, досить малого, щоб задовільно виміряти найменший з островів.
Співвідношення (2.32) застосовується при дослідженні геометрії хмар і зон дощу, розміри яких заключені в широких межах від 1 до ![]()
![]() . З'ясувалося, що периметр хмари пов'язаний з його площею співвідношенням (2.32) з фрактальним розміром D = 1,35 ± 0,05. При цьому ці оцінки виявилися справедливі як для купчастих, так і для пір'ястих хмар. У роботі А. Вальдфогеля, присвяченій аналізу фрактальної розмірності хмар з потужними конвективними струмами, було встановлене співвідношення між периметром і площею для послідовності моментів часу (з інтервалом в 1 хвилину) у площині перетину для постійного коефіцієнта відбиття. Основні висновки можуть бути наступними: для хмар, периметр яких більше 8 км, розмір фрактала приблизно збігається з розміром менш потужних хмар і становить 1,36 ± 0,1; для хмар з периметром від 3 км до 8 км D=1,0 ± 0,1 і, нарешті, хмари з периметром менш 3 км не є фракталами.
. З'ясувалося, що периметр хмари пов'язаний з його площею співвідношенням (2.32) з фрактальним розміром D = 1,35 ± 0,05. При цьому ці оцінки виявилися справедливі як для купчастих, так і для пір'ястих хмар. У роботі А. Вальдфогеля, присвяченій аналізу фрактальної розмірності хмар з потужними конвективними струмами, було встановлене співвідношення між периметром і площею для послідовності моментів часу (з інтервалом в 1 хвилину) у площині перетину для постійного коефіцієнта відбиття. Основні висновки можуть бути наступними: для хмар, периметр яких більше 8 км, розмір фрактала приблизно збігається з розміром менш потужних хмар і становить 1,36 ± 0,1; для хмар з периметром від 3 км до 8 км D=1,0 ± 0,1 і, нарешті, хмари з периметром менш 3 км не є фракталами.
Мандельброт запропонував не тільки визначення фракталів, але також і алгоритм побудови одного з них, що получили назву на честь ученого. Алгоритм побудови множини Мандельброта заснований на ітеративному обчисленні за формулою:
![]()
де Z і C – комплексні змінні. Ітерації виконуються для кожної стартової точки C прямокутної або квадратної області – підмножині комплексної площини. Ітераційний процес триває доти, поки ![]() не вийде за межі окружності заданого радіуса, центр якої лежить у точці (0,0), або після досить великої кількості ітерацій. Залежно від кількості ітерацій, протягом яких
не вийде за межі окружності заданого радіуса, центр якої лежить у точці (0,0), або після досить великої кількості ітерацій. Залежно від кількості ітерацій, протягом яких ![]() залишається усередині окружності, встановлюється колір точки C. Якщо
залишається усередині окружності, встановлюється колір точки C. Якщо ![]() залишається усередині окружності протягом досить великої кількості ітерацій, то ця точка растра зафарбовується в чорний колір. Множині Мандельброта (рис. 2.12) належать саме ті точки, які протягом безкінечного числа ітерацій не переходять у безкінечність.
залишається усередині окружності протягом досить великої кількості ітерацій, то ця точка растра зафарбовується в чорний колір. Множині Мандельброта (рис. 2.12) належать саме ті точки, які протягом безкінечного числа ітерацій не переходять у безкінечність.
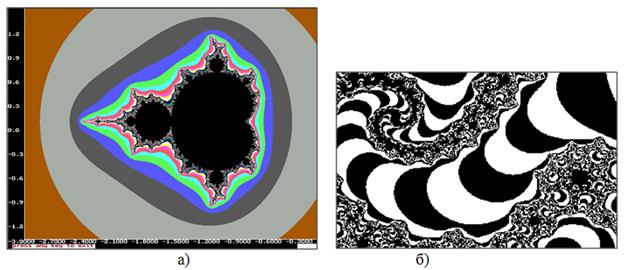
Рисунок 2.12 – а) Множина Мандельброта; б) Збільшена ділянка границі множини Мандельброта
Побудова іншої фрактальної множини, сніжинки Коха (рис. 2.13), починається із правильного трикутника, довжина сторони якого дорівнює 1. Сторона трикутника вважається базовою ланкою для вихідного положення. Далі, на будь-якому кроці ітерації кожна ланка заміняється на утворюючий елемент – ламану, що складається по краях з відрізків довжиною 1/3 від довжини ланки, між якими розміщаються дві сторони правильного трикутника зі стороною в 1/3 довжини ланки. Всі відрізки – сторони отриманої кривої вважаються базовими ланками для наступної ітерації. Крива, що одержується в результаті n-ї ітерації при будь-якому кінцевому n, називається передфракталом, і лише при n, що наближається до безкінечності, крива Коха стає фракталом. Отримана в результаті ітераційного процесу фрактальна множина є лінію нескінченної довжини, що обмежує кінцеву площу. Дійсно, при кожному кроці число сторін результуючого багатокутника збільшується в 4 рази, а довжина кожної сторони зменшується тільки в 3 рази, тобто довжина багатокутника на n- й ітерації дорівнює ![]() і прагне до безкінечності з ростом n.
і прагне до безкінечності з ростом n.
|
|
|
|
|
Рисунок 2.13 – Перші 5 поколінь сніжинки Коха
Площа під кривою, якщо прийняти площу утворюючого трикутника за 1, дорівнює:
![]()
З недавнього часу фрактальні методи почали використовувати при розробці методів розпізнавання образів на радіолокаційних зображеннях. Суть їх полягає в наступному. Важко локалізувати танк замаскований серед кущів. Важко, навіть коли є якісний сигнал від теле- та теплотелевізора. Набагато легше зробити це за допомогою фрактальних методів. Як вже було сказано вище, обриси штучних об’єктів – танків, автомобілів – створені лініями, які описуються рівняннями цілого порядку. А ось об’єкти природні – рельєф, дерева – фрактальні, тобто мають фрактальну розмірність. Ось на цьому принципі і побудовані нові системи розпізнавання образів. Системи розпізнавання не бачать кущ, але дуже добре розпізнають штучний об’єкт, схований за кущом. Маскувальне забарвлення може допомогти, але якщо воно не створене кривими другого порядку, як звичайно.
Іншими словами, якщо ми виміряємо розмірність зображення якогось природного ландшафту, то вона буде дробова. Розмірність геометричної фігури рівна близько 2 (через похибку вимірювання). А коли накласти, наприклад, прямокутник (як це показано на рисунку 2.14) на природне зображення, то розмірність всієї картинки різко поміняється.

Рисунок 2.14 – Розрахунок розмірності зображення
Основною перевагою даного методу над іншими є те, що не потрібно витрачати зусилля і час на покращення якості зображення. Це не дуже впливає на результат. Інша перевага полягає в нижчій вимозі до високої роздільної здатності зображень, порівняно з іншими методами. На результат впливає лише площа, яку займає штучний об’єкт на зображенні, а не контраст, як звичайно.
Самоподібність (self-similarity) є основною характеристикою фракталу і означає, що він більш-менш одноманітно побудований у широкому діапазоні масштабів. Так, при збільшенні, маленькі фрагменти фракталу виходять дуже схожими на більші. В ідеальному випадку така самоподібність приводить до того, що фрактальний об'єкт є інваріантним до збільшень.
Звичайно, для реального природного фракталу існує деякий мінімальний масштаб довжини lmin, такий, що на відстанях l≈lmin, його основна властивість — самоподібність — пропадає. Крім того, на досить великих масштабах довжин l>lmax, де lmax — характерний геометричний розмір об'єктів, ця властивість самоподібності також порушується. Тому властивості природних фракталів розглядаються лише в масштабах l, що задовольняє співвідношенню lmin«l«lmax.
Відмітимо, що властивість точної самоподібності характерна лише для регулярних фракталів. Якщо замість детермінованого способу побудови включити в алгоритм їхнього створення деякий елемент випадковості (як це буває, наприклад, у багатьох процесах дифузійного росту кластерів, електричному пробої й т.д.), то виникають так звані випадкові фрактали. Основна їхня відмінність від регулярних полягає в тому, що властивості самоподібності справедливі тільки після відповідного усереднення по всім статистично незалежним реалізаціям об'єкта. При цьому збільшена частина фракталу не точно ідентична вихідному фрагменту, однак їхні статистичні характеристики збігаються.
Стиск зображень (image compression). За допомогою фракталів можна стискувати зображення з деякою втратою якості, аналогічно іншим методам стику з втратами. Але фрактальний стиск дає кращі результати. Методи компресії, основані на RLE, класичний алгоритм Хаффмана, LZW, не враховують природи стискуваних даних і тому дають незадовільні результати при обробці зображень. Фрактальний стиск зображень – це алгоритм стиску зображень з втратами, заснований на застосуванні систем ІFS до зображень. Даний алгоритм відомий тим, що в деяких випадках дозволяє одержати дуже високі коефіцієнти стиску (кращі приклади – до 1000 разів при прийнятній візуальній якості) для реальних фотографій природних об'єктів, що недоступно для інших алгоритмів стиску зображень у принципі.
Основна проблема фрактального стиску – це те, що компресія-декомпресія виконується швидко і однозначно, в той час, як пряма процедура потребує від машини великих інтелектуальний можливостей. При компресії можна не зберігати оригінальні розміри зображення, достатньо просто запам’ятати їх відношення. А при декомпресії – задавати ті розміри, які нам найбільше підходять. Така можливість дозволяє вирішити задачу екстраполяції початкового зображення. При встановленні нових розмірів, що перевищують старі, в нове зображення добавляються елементи, подібні іншим елементам зображення. І якщо, оброблюється природній об’єкт (наприклад, гранітний камінь), то заміна не буде помітною.
Основа методу фрактального кодування – це виявлення самоподібних ділянок у зображенні. Патенти ідеї були отримані в 1990-1991 роках.
Суть фрактального стиску. В основі більшості методів фрактального кодування, що застосовуються сьогодні, використовуються системи доменних і рангових блоків зображення, блоків квадратної форми, що покривають все зображення. Фрактальне кодування напівтонових зображень основане не гіпотезі, згідно з якою, в будь-якому зображенні можна знайти локальну самоподібність різних його частин. Існуючі алгоритми фрактального стиску, як правило, притримуються наступної схеми кодування. Зображення, яке кодується розбивається на множину блоків, що не перекриваються (рангові області), для кожного з яких, в межах цього ж зображення, відшукується блок більшого розміру (домен), пікселі якого, шляхом деякого перетворення, переводились би в пікселі рангової області. При цьому для пошуку оптимальної відповідності рангових областей і доменів необхідний повний перебір варіантів, що веде за собою значні обчислювальні затрати. З перетворень, що переводять домени в рангові області, формується відображення, що переводить зображення в зображення. При цьому, кодом зображення буде місце розташування і розміри рангових областей, а також коефіцієнти перетворень, описуючих самоподібність всередині зображення. Кількість біт, необхідних для опису коду, буде значно менше кількості біт, необхідних для опису початкового зображення. Коефіцієнтом стиску називається відношення бітового представлення зображення до бітового представлення коду. В відомих фрактальних методах стиску зображень значення цього коефіцієнту може досягати 100 при достатньо непоганій якості відновлення. Для відновлення закодованого таким чином зображення використовується принцип стиснених відображень, який говорить, що стискуюче відображення, діюче в повному метричному просторі, має єдину нерухому точку. Відображення, що діє на повному метричному просторі зображень, формується з перетворень, які переводять домени в рангові області [3].
Відповідно до даного методу зображення розбивається на безліч неперекриваючих рангових підзображень і визначається безліч перекриваючих доменних підзображень. Для кожного рангового блоку алгоритм кодування знаходить найбільш підходящий доменний блок і афінне перетворення, що переводить цей доменний блок у даний ранговий блок. Структура зображення відображається в систему рангових блоків, доменних блоків і перетворень.
Основна складність фрактального стиску полягає в тому, що для знаходження відповідних доменних блоків, загалом кажучи, потрібен повний перебір. Оскільки при цьому переборі щораз повинні рівнятися два масиви, дана операція виходить досить тривалою. Порівняно простим перетворенням її можна звести до операції скалярного добутку двох масивів, однак навіть скалярний добуток рахується порівняно тривалий час.
Крім стиску, іншою областю фрактальної обробки зображень є їх генерація. В наш час існує множина найрізноманітніших пакетів прикладних програм від простих, які створюють зображення на основі множини Мандельброта (Fractal SSE), до складних, які генерують зображення 3d, анімаційні зображення та IFS-зображення. Всі вони побудовані на основі відкриття Мандельброта: якщо нанести визначені точки на площину комплексних чисел, то можна створювати зображення надзвичайного абстрактного вигляду – множина Мандельброта. В рівняння Мандельброта підставляються координати деякої точки комплексної площини, і результатом є координати іншої точки. Результат, отриманий при вводі координат першої точки, слугує початком для наступної ітерації, її результат підставляється в наступне рівняння і так далі. Обидві ці найголовніші області застосування фрактальних методів в наш час знаходяться на порівняно високому рівні розвитку, незважаючи на те, що фрактальна наука досить молода. Існує надзвичайно велика кількість програм, за допомогою яких можна створити або стиснути зображення і ефективність обробки зображень деяких з цих програм достатньо висока.
Потенційним, хоч і менш відомим видом фракталів, є фрактали на основі системи ітераційних функцій (Iterated Function System – IFS). Метод IFS, який застосовується до побудови фрактальних зображень, винайшов Майкл Барнслі. Він базується на самоподібності елементів зображення і полягає в моделюванні малюнка декількома меншими частинами його самого. Найвідомішим IFS-зображенням є чорний папоротник, в якому кожен лист в дійсності являє собою мініатюрний варіант самого папоротника [4].
Система IFS – це також сукупність стискаючих афінних перетворень. Як відомо, афінні перетворення містять у собі масштабування, поворот і паралельний перенос. Афінне перетворення вважається стискаючим, якщо коефіцієнт масштабування менше одиниці.
Розглянемо докладніше побудову кривій Кох з використанням афінних перетворень. Кожний новий елемент кривої містить чотири ланки, отриманих з утворюючого елемента використанням масштабування, повороту й переносу.
1. Для одержання першої ланки досить стиснути вихідний відрізок у три рази. Слід зазначити, що те ж масштабування застосовується для всіх ланок.
2. Наступна ланка будується з використанням всіх можливих перетворень, а саме: стиск у три рази, поворот на – 60 градусів і паралельний перенос на 1/3 по осі X.
3. Третя ланка будується аналогічно другому: стиск у три рази, поворот на 60 градусів, паралельний перенос на 2/3 по осі X.
4. Остання ланка: стиск у три рази, паралельний перенос на 2/3 по осі X.
Для синтезу фрактала вибирається початкова точка, до якої застосовується випадковим образом обране з ІFS перетворення, у результаті чого точка переміщується в інший кінець екрана. Ця операція повторюється багато разів (досить 100 ітерацій), і через деякий час точка починає блукати по атрактору (безліч всіх можливих траєкторій), що і буде являти собою зображення фрактала. Кожне нове положення точки зафарбовується кольором, відмінним від фону. Існує теорема, яка доводить, що отриманий атрактор буде замкнутим. Для того, щоб блукаюча точка зафарбовувала нові пікселі, а не блукала по старим, використовують сьомий параметр, що являє собою ймовірність появи конкретного афінного перетворення з набору перетворень ІFS. Якщо вибрати початкову точку так, щоб вона відразу виявилася на атракторі, то вона починає блукати в області цього атрактора, не переміщуючись в інші області екрана. Розглядаючи кожне перетворення окремо, можемо помітити, що де б ми не починали, після декількох ітерацій, точка перестане рухатися по екрану. Точка зупинки називається нерухомою точкою – це розв’язок системи лінійних рівнянь двох змінних, яке знаходиться методом простої ітерації. Нерухома точка кожного перетворення входить до складу атрактора. Тому за початкову точку при побудові фрактала можна взяти нерухому точку першого перетворення з набору ІFS.