
8.4. Нейронні мережі в задачах обробки зображень
Для розпізнавання складних об’єктів створюють системи на основі нейронних мереж (НМ, neural network). Вони можуть мати топологію, орієнтовану на розв’язання конкретної задачі із врахуванням властивостей об’єкта – просторово-часову орієнтацію, масштаб, геометричні параметри об'єкта, включаючи координати, кутове положення, лінійний розмір, відстань, тощо. У той же час істотним недоліком типових НМ є відсутність ефективних засобів для розв’язання задач розпізнавання динамічних образів. Основною проблемою інтерпретації динамічних візуальних сцен є висока розмірність простору ознак, наявність геометричних перетворень над об'єктом. Стиск простору ознак виконують методом витягу інтегральних і інваріантних до геометричних перетворень параметрів зображень. Метод геометричних та більш загальних алгебраїчних інваріантів відіграє значну роль у розв’язанні задач розпізнавання зображень. Так, наприклад, інваріанти, у тому числі інваріантні моменти, були успішно використані для розпізнавання профілів літаків і танків, друкованих і рукописних букв, параметрів стикувального вузла космічного апарата, а також багатьох інших об'єктів. Математичне обґрунтування інваріантних особливостей напівтонових зображень базується на теорії алгебраїчних інваріантів.
Суть НМ полягає в тому, що мережа складається з елементів, котрі називаються формальними нейронами (formal neuron). Кожен нейрон приймає набір сигналів, що надходять на його входи від одної групи таких же нейронів, обробляє сигнали з врахуванням попередніх сигналів і адаптації до них на основі процедур навчання і передає результати обробки другій групі нейронів. Зв'язки між нейронами кодуються вагами, що відображають важливість їх інформації для визначення загального результату. Основний принцип настроювання нейронної мережі полягає в застосуванні процедур оптимізації та адаптації на основі певних критеріїв, здатності до перенавчання. Однією з переваг НМ є те, що всі елементи можуть функціонувати паралельно, тим самим істотно підвищуючи ефективність розв’язання задач, особливо при обробці зображень в реальному часі. Системи розпізнавання об'єктів зображення, що засновані на нейронних мережах, використовують ієрархічну архітектуру. Спочатку вектор ознак обробляється грубою з високим рівнем похибок, але швидкою, мережею, далі, якщо вектор не був класифікований як не об'єкт, алгоритм розв’язання коректується більш точною і більш повільною мережею.
Переважна кількість прикладних нейронних систем передбачає використання багатошарових персептронів (назва „персептрон” походить з англійського perceptron – сприйняття, оскільки перші зразки таких структур призначались для моделювання зору). Популярність персептронів зумовлена широким колом доступних для них задач. Загалом вони вирішують задачу апроксимації багатовимірних функцій, іншими словами – побудову багатовимірного відображення F : x→y , яке узагальнює заданий набір прикладів (еталонних пар даних) {xa ,ya } .
Залежно від типу вихідних змінних (тип вхідних не має вирішального значення), апроксимація функції може набувати вигляду:
Множина практичних задач розпізнавання зображень, фільтрації шумів, передбачення часових рядів та інші зводяться до цих базових задач.
Розглянемо алгоритм навчання персептрона на простій модельній задачі. Персептрон навчають, подаючи сукупність (множину) зображень по одному на його вхід і змінюють ваги доти, доки для всіх зображень не буде досягнуто необхідний вихід. Припустимо, що вхідні зображення нанесено на демонстраційні карти. Кожну карту розбито на квадрати і від кожного квадрата на персептрон подається вхідний сигнал. Якщо в квадраті є лінія, то від неї подається одиниця, у протилежному випадку – нуль. Сукупність квадратів на карті задає сукупність нулів і одиниць, котрі подаються на входи персептрона. Мета полягає в тому, щоб навчити персептрон вмикати індикатор за умови подавання на нього сукупності входів, що задають непарне число, і не вмикати у випадку парного. На рисунку 2.20 показана така персептронна конфігурація.
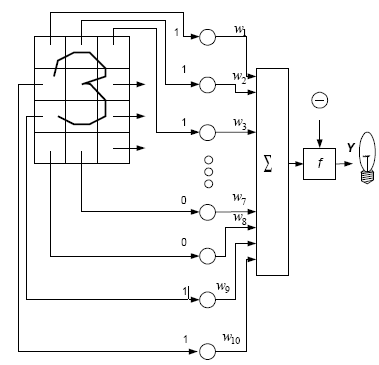
Рисунок 2.20 – Персептронна система розпізнавання зображень
Припустимо, що вектор x є зображенням демонстраційної карти, яка піддається розпізнаванню. Кожну компоненту xi (квадратик зображення карти) вектора x перемножують на відповідну компоненту wi вектора ваг w . Ці добутки сумують. Якщо сума перевищує поріг q , то вихід нейрона y дорівнює одиниці (індикатор запалюється), у протилежному випадку – нуль. Цю операцію компактно записують у векторній формі: y = xw . Для навчання мережі образ x подають на вхід і обчислюють вихід y . Якщо вихід правильний, то нічого не змінюється. Однак якщо вихід неправильний, то ваги, приєднані до входів, що підсилюють помилковий результат, модифікуються, щоб зменшити помилку.
Пересвідчимось, як це відбувається. Припустимо, що демонстраційна карта з цифрою 3, подана на вхід і вихід y , дорівнює одиниці (мережа вказує на непарність). Оскільки це правильна відповідь, то ваги не змінюються. Якщо на вхід подають карту з номером 4 і вихід y дорівнює одиниці (непарне число), то ваги, приєднані до одиничних входів, повинні бути зменшені, оскільки вони прагнуть дати невірний результат. Аналогічно, якщо карта з номером 3 дає нульовий вихід, то ваги, приєднані до одиничних входів, необхідно збільшити, щоб скорегувати помилку.
За скінчене число кроків мережа навчиться розділяти карти на парні і непарні за умови, що сукупність цифр лінійно роздільна. Отже для всіх непарних карт вихід буде більшим від порогу, а для всіх парних – нижчим. Зазначимо, що це навчання глобальне, тобто мережа навчається на всій можливій множині вхідних сигналів.
Причина популярності персептронів в тому, що для свого кола задач вони є універсальними та ефективними з погляду обчислювальної складності пристроями.
Недоліком використання нейронних мереж є їх перенавантаження при надмірному збільшенні кількості нейроні у мережі. Іншим недоліком є те, що існує великий клас функцій, які неможливо розділити за допомогою одношарової мережі. Про ці функції говорять, що вони є лінійно нероздільними, і саме вони накладають вагомі обмеження на можливості одношарових мереж.
Контрольні запитання та завдання
1. У чому полягає сутність поелементної обробки зображень ?
2. Доведіть тотожність прямого й зворотного двовимірних ДПФ.
3. Поясніть, чому при обмеженому розмірі околу, що застосовується при КІХ-фільтрації, не можна досягти граничного придушення шуму ?
4. Назвіть умови, при виконанні яких інверсна фільтрація забезпечує високу якість відновлення зображень.
5. Яка структура двовимірного частотного спектра дискретного зображення?
6. При яких умовах, використовуючи дискретне зображення, можна без втрат відновити безперервне?
7. Доведіть, що двовимірний фільтр із прямокутною частотною характеристикою ідеально відновлює безперервне зображення з дискретного.
8. Які методи покращення якості зображення ви знаєте?
9. Реалізуйте в ППП Matlab метод покращення якості зображення шляхом вирівнювання гістограми яскравості пікселів за допомогою функції Image Processing Toolbox – histeq.
10. За допомогою яких функцій можна накласти сторонній шум на зображення? Які види шуму ви знаєте?
11. В чому полягає суть двовимірної згортки зображення?
12. Розгляньте використання функції roifill для усунення дефектів напівтонового зображення.
13. Реалізуйте за допомогою функції nlfilter операцію усереднення з порогом, в цілях фільтрації імпульсного шуму.
14. Перевірте чи є зображення напівтоновим, бінарним, палітровим чи повнокольоровим за допомогою функцій isind, isgray, isrgb,isbw.
15. Реалізуйте перетворення повнокольорового зображення в напівтонове, а напівтонового в палітрове за допомогою функцій im2double, gray2ind.
16. Порівняйте алгоритми побудови множини Мандельброта та сніжинки Коха.
17. Який показник використовується для зв’язку фрактальної та топологічної розмірності?
18. Порівняйте алгоритми стиску зображень (RLE, Хаффмана, LZW). В чому полягає особливість фрактального стиску зображень?
19. Поясните поняття: розмірність Хаусдорфа-Безиковича деякої множини А
20. Які перетворення називаються масштабними? Міра Хаусдорфа має властивість інваріантності щодо масштабних перетворень?
21. Сформулюйте загальні вимоги, яким повинна задовольняти розмірність множини при будь-якому способі виміру цієї множини.
22. На основі яких функцій будуються найбільш поширені материнські базиси? Чим це обумовлено?
23. Яким чином виконується пряме вейвлет-перетворення?
24. Порівняйте процедури компресії зображення за допомогою ДВП та фрактальних методів.
25. Чим відрізняються нейронні мережі від інших типів мереж?
26. Яким образом відбувається навчання нейронної мережі?