Динамічне програмування

10.10 Динамічне програмування

На практиці часто доводиться зустрічатись з випадками, коли метою (ціллю) оптимізації є встановлення найкращої послідовності тих чи інших робіт (виробничих операцій, етапів будівництва різних споруд тощо). З подібною метою зустрічаються при розв’язанні задач так званого динамічного програмування.

Однією з перших задач такого роду, що привернули увагу математиків, була так звана задача про комівояжера (мандрівного торговця). Суть її така: є міст з заданими між ними відстанями . Потрібно, відправившись з , вибрати такий маршрут пересування , при якому комівояжер, побувавши в кожному місті по одному разу, повернувся б до вихідного пункту , пройшовши при цьому мінімально можливий сумарний шлях.

Основний спосіб динамічного програмування полягає в знаходженні правил домінування, які дозволяють робити порівняння варіантів розвитку послідовностей і завчасне відсіювання безперспективних варіантів. У ряді випадків в задачах динамічного програмування вдається одержати такі сильні правила домінування, що вони визначають елементи оптимальної послідовності однозначно один за одним. В такому випадку правила домінування називають розв’язувальними правилами.

Розв’язувальні правила звичайно виводяться за допомогою принципу оптимальності Беллмана. Суть принципу оптимальності така. Нехай критерій (задається формулою або алгоритмом), який дає числову оцінку якості варіанта (послідовності) , можна застосовувати не тільки до всієї послідовності, але і до будь-якого її початкового відрізку . Послідовність , якій відповідає екстремальне значення критерію , називається оптимальною. Якщо будь-який початковий відрізок оптимальної послідовності також оптимальний (в класі всіх послідовностей, складених з тих же елементів, і можливо, такий, що має ті ж початок і кінець, що і даний відрізок), то вважають, що для відповідної задачі справедливий принцип оптимальності.

Розглянемо зразок розв’язання задачі про комівояжера методом динамічного програмування:

1. Введення даних про пункти і відстані між пунктами i та j d_ij(d_ij=0 при i=j) .

2. Обчислення всіх можливих варіантів відстаней, що складаються з трьох дільниць A_0, A_i1, A_i2, A_i3. Вони групуються по останньому пункту і з них залишаються ті варіанти, що об’єднують однакові пункти, але мають найменший шлях.

3. До тих варіантів, що залишились додають ще четверту дільницю і повторюють процедуру з пункту 2. Це повторюється для п’ятої, шостої і т. д. дільниць, доки не повертається в пункт А₀. Той варіант (чи варіанти), що залишилися, і визначають найкоротший шлях, по якому комівояжеру можна об’їздити всі місті А_i (i=0,…,n), якщо він почне та закінчить свою подорож в А_0.

10.11 Варіаційні задачі

В варіаційних задачах місце змінних займають функції, а критерій оптимізації – деяка дійсна функція, що залежить від цих функцій і називається функціоналом.

В найпростішому випадку мають справу з функцією однієї змінної і функціоналом вигляду

де і – константи, – задана функція трьох дійсних змінних. При цьому припускається, що як сама функція , так і її похідна неперервні на відрізку .

В класичному варіаційному численні доводиться, що екстремум функції (мінімум або максимум) функціонала досягається на функціях , які задовольняють диференціальне рівняння, тобто рівняння Ейлера:

Тут через і ( або ) позначені, відповідно, перша і друга частинні похідні функції по змінній і по змінним .

10.12 Системна оптимізація

В практиці проектування великих систем і управління такими системами, як правило, використовується багато критеріїв. В ряді випадків їх вдається в той чи іншій спосіб звести до одного критерію і тим самим повернутися до вже дослідженого випадку однокритеріальної оптимізації.

Найпростіший спосіб такого зведення – так зване зважування критеріїв. Якщо функції, що виражають значення використовуваних критеріїв, то кожній з них, відповідно до відносної важливості критеріїв, вибирається додатний ваговий коефіцієнт . Операція зважування критеріїв (цільових функцій) полягає в заміні їх єдиним критерієм (цільовою функцією) .

Але для багатьох задач, що пов’язані з великими системами, подібне зведення виявляється практично неможливим, так що в процесі оптимізації доводиться мати справу з векторною (багатокритеріальною) цільовою функцією. При цьому припустима область може змінюватись в процесі оптимізації. Більше того, в її цілеспрямованій зміні як раз і полягає основна змістовна сутність процесу оптимізації для подібного класу задач.

Наведемо одну з характерних формалізованих постановок задачі системної оптимізації.

Розв’язок відшукується безпосередньо в просторі критеріїв оптимізації, які ми позначимо і . Процес розв’язання починається з того, що в заданому просторі вибирається деяка точка з координатами – бажаний розв’язок задачі. За цим будуються початкові обмеження , що задають початкову припустиму область . Прямою перевіркою встановлюється, чи належить точка області . В першому випадку в принципі може бути застосована звичайна (класична) процедура оптимізації або за одним з критеріїв, , або за тією чи іншою їх комбінацією.

Але при системному підході застосовується звичайно запропонований Л. С. Понтрягіним спосіб, а саме: відповідно до моделі вищого рівня, що управляє вибором критеріїв, точка виводиться з границь припустимої області , як це показано на рисунку 5.4.

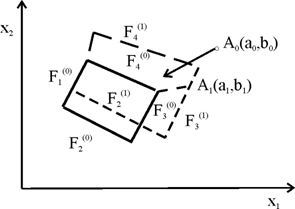
Рисунок 5.4 – Виведення точки

Після цього виділяються ті обмеження, які не виконуються в точці (в випадку, що розглядається, ними будуть і ). Звертаючись до моделей і , які формують ці обмеження, в діалоговому режимі опробовуються ті чи інші рішення, що змінюють відповідні обмеження в потрібному напрямку (якщо така зміна можлива). Оптимальним при цьому вважається той напрямок, що зменшує абсолютну величину від’ємних відхилень (в випадку, який розглядається, і ).

10.13 Застосування теорії графів до розв’язання оптимізаційних задач

Розв’язання багатьох технічних задач можливо методами теорії графів. Основні поняття та визначення теорії графів розглянуті в відповідних підручниках, які є в списку літератури в кінці цієї книжки. Тут ми обмежимося розглядом підходів до транспортної задачі та задачі комівояжера з застосуванням теорії графів.

Ці підходи базуються на відомій задачі з теорії графів про знаходження найкоротшого шляху між двома вершинами зв’язного неорієнтованого графу. До цієї задачі зводяться не тільки задача про комівояжера чи транспортна, а також, наприклад, багато задач оптимальної обробки деталей, оптимізації програмування, управління динамічними системами і т.д. В загальному вигляді задача формулюється так. Дано неорієнтований граф , де – множина вершин, – множина ребер. Кожному ребру приписане деяке число , що називається довжиною ребра (в транспортних задачах це може бути час чи вартість проїзду цим ребром). Треба для будь-яких вершин і графу знайти такий шлях, що його довжина буде найкоротшою.

Загальне правило виявлення найкоротшого шляху в графі полягає в тому, щоб кожній вершині приписати індекс , який дорівнює довжині найкоротшого шляху з даної вершини до кінцевої. Якщо, наприклад, спочатку взяти граф з ребрами одиничної довжини, то порядок дій буде такий:

1. Кінцевій вершині присвоюється індекс ;

2. Усім вершинам, з котрих йде ребро до кінцевої вершини, присвоюється індекс 1;

3. Усім вершинам, що не мають індексів, та з котрих йде ребро в вершину з індексом , приписується індекс . Цей процес продовжується до тих пір, поки не буде помічена початкова вершина.

Після закінчення цього процесу індекс початкової вершини буде дорівнювати довжині найкоротшого шляху, а найкоротший шлях знаходиться, якщо пересуватися з початкової вершини в напрямку зменшення індексів. Приклад наведено на рисунку 5.5. Подвійною лінією наведені два найкоротших шляхи.

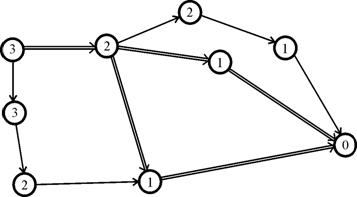
Рисунок 5.5 – Знаходження найкоротшого шляху в графі з ребрами одиничної довжини

Тепер розглянемо випадок, коли ребра мають довільну довжину. Процес присвоювання індексів ускладнюється, і порядок дій може бути зведений до такого:

1. Кожній вершині присвоюється індекс . Спочатку кінцевій вершині присвоюється індекс . Для інших вершин беремо на першому кроці .

2. Шукаємо таку дугу , що , й замінюємо індекс на індекс . (Нагадаємо, що - довжина дуги). Процес заміни індексів продовжується до тих пір, поки залишиться хоча б одна дуга, для якої можна зменшити .

Відзначимо дві важливі властивості індексів:

1. Нехай – довільне ребро. Для нього обов’язково виконується умова . Це виходить з того, що при невиконанні умови індекс треба було б зменшити.

2. Нехай – довільна вершина. При реалізації алгоритму присвоювання індексів індекс монотонно зменшується. Нехай – остання вершина, що була використана для його зменшення. Тоді . Це приводить до висновку, що для будь-якої вершини з індексом може бути знайдено вершину , що з’єднується ребром з , таку, що .

Виявлені властивості дають можливість сформулювати такий спосіб знаходження найкоротшого шляху.

Нехай – початкова вершина з індексом . Шукаємо вершину таку, що . Далі шукаємо вершину таку, що , і т.д. до тих пір, поки не дійдемо до кінцевої вершини. Шлях – найкоротший. Приклад використання цього способу поданий на рисунку 5.6. Найкоротший щлях виділений подвійною рискою.

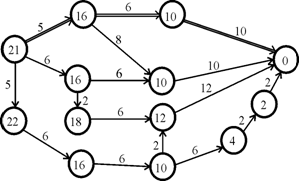
Рисунок 5.6 – Знаходження найкоротшого шляху в графі з ребрами довільної довжини.

Очевидно, ці задачі про пошук найкоротшого шляху в графі аналогічні деяким задачам, що виникають в різних практичних областях. До неї зводяться задачі про побудову доріг, що з’єднують декілька міст найдешевшим чином, задачі про розбудову електромережі, нафтопроводів та ін. За допомогою графових підходів можна розв’язавши транспортну задачу та задачу про комівояжера. Розглянемо задачу про комівояжера у вигляді графу. Вершини цього графу відповідають містам, а шляхи - дорогам, що ці міста з’єднують. Кожній дузі можна приписати довжину, що дорівнює відстані між містами. І далі дуже просто звести задачу комівояжера до задачі про пошук найкоротшого шляху. До задачі про комівояжера зводиться багато транспортних задач, задач оптимізації програмування, оптимізації порядку оброблення деталей та ін.