10.5     Опукла оптимізація

 

Задача оптимізації може бути значно спрощена при накладанні на цільову функцію і припустиму область деяких обмежень. Одним з таких обмежень є так звана умова опуклості.

Множина евклідового простору називається опуклою, якщо для будь-яких двох точок і цієї множини всі точки відрізку , що їх з’єднує, також належать множині .

    

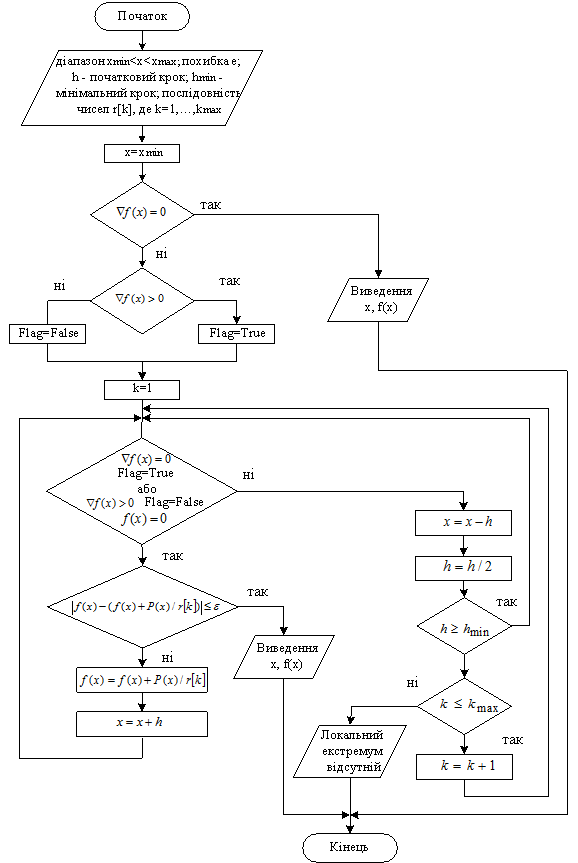
Рисунок 5.3 – Алгоритм методу штрафних функцій

 

Функція опукла, або, точніше, опукла донизу, якщо вона визначена на опуклій множині і для будь-яких двох точок і цієї множини значення функції в будь-якій точці відрізка не перевищують значення в тій же точці, що визначена на даному відрізку

лінійної функції із значеннями і на його кінцевих точках. Це, в загальному випадку, виражається нерівністю

при .

Очевидно, що при вираз задає різні точки відрізка .

Для опуклої функції в будь-якій точці , що лежить в області визначення функції, існує вектор , для якого при будь-якому і виконується нерівність

В правій частині цієї нерівності стоїть скалярний добуток векторів і , тобто добуток довжин цих векторів на косинус кута між ними. Вектор , що задовольняє цю властивість, називається узагальненим градієнтом (субградієнтом) функції в точці . Звичайний градієнт (у випадку його існування і відмінності від нуля) є також узагальненим градієнтом, причому єдиним, в розглядуваній точці. Якщо функція не диференційовна в деякій точці , в ній існує деяка множина узагальнених градієнтів, яку називають субградієнтною множиною функції в точці .

 

10.5.1 Простий субградієнтний метод опуклої оптимізації

 

Для реалізації субградієнтної оптимізації в випадку задачі без обмежень процес може починатися з будь-якої точки . Зсув чергової точки до наступної точки здійснюється на відстань в напрямку будь-якого узагальненого градієнта функції в точці в випадку задачі максимізації вгнутої функції і в зворотному напрямку – у випадку задачі мінімізації опуклої функції. Якщо кроки зсувів обираються таким чином, що при , а ряд розбігається, то послідовність збігається до множини екстремуму заданої функції за умови, що множина обмежена.

Для обчислення субградієнтів застосовуються різні способи. Одним з них є зведення задачі обчислення субградієнта функції, що задана складним виразом, до обчислення субградієнтів окремих компонентів цього виразу. Для подібного зведення особливо часто застосовуються такі властивості опуклих функцій.

Властивість 1. Якщо функції опуклі, то опуклою буде і будь-яка їх лінійна комбінація з невід’ємними коефіцієнтами , а субградієнт функції дорівнює лінійній комбінації субградієнтів функцій .

Властивість 2. Якщо функції опуклі, то опуклою буде і функція , і всі субградієнтні множини функцій , для яких , входять в субградієнтну множину функції в будь-якій заданій точці .

 

10.5.2 Методи розтягу простору

 

Простий субградієнтний метод, що розглянутий в попередньому розділі, може виявитися повільно збіжним, якщо області рівня цільової функції сильно витягнуті в одному напрямку, або, як часто при цьому говориться, мають вигляд вузьких і довгих ярів. Ця ситуація характерна для багатьох задач негладкої оптимізації. Для поліпшення збіжності методу в подібних випадках використовують методи розтягу простору.

Розтяг простору зводиться до заміни змінних в цільовій функції деякими їх лінійними комбінаціями. Особливо просто виконується розтяг в напрямку однієї з координатних осей. Змінна , що відповідає цій осі, замінюється при цьому на , де - коефіцієнт розтягу, а решта залишається без змінювання.