Додаток А
Чисельний розрахунок деяких задач
Приклади до розділу 1. Математичне моделювання
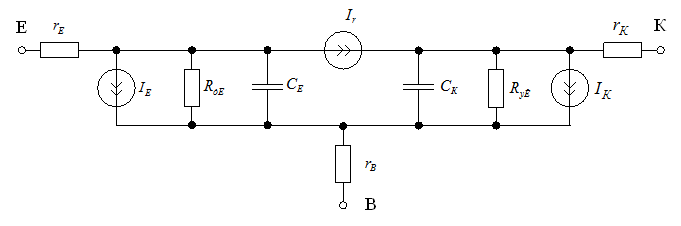
Приклад 1.1. Математична модель біполярного транзистора. Розглянемо еквівалентну схему біполярного транзистора. Прийняті наступні позначення: 
– відповідно елементи p-n переходів емітер-база і колектор-база; 
– джерело струму, що відображає проліт неосновних носіїв через базу і визначає підсилювальні властивості транзистора (
і 
– нормальний і інверсний коефіцієнти підсилення струму); 
і 
– об'ємні опору областей емітера, колектора і бази.
Запишемо компонентні рівняння для кожного елементу. Отримаємо наступну систему рівнянь:
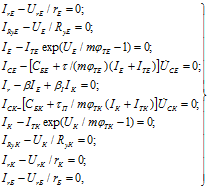
де 
– тепловий струм переходу база-емітер; m – емпіричний коефіцієнт; 
– температурний потенціал емітера; 
– бар'єрна ємкість переходу база - емітер; 
– бар'єрна ємкість переходу база - колектор; 
– температурний потенціал колектора; 
– тепловий струм переходу база - колектор; 
– параметри, що характеризують час прольоту носіїв струму через області транзистора.
Невідомими змінними в цьому випадку є
.
З цього переліку виходить, що в моделі враховані деякі топологічні рівняння: виключені величини 
і 
і 
величини, які співпадають відповідно з величинами 
і 
.
Запишемо топологічні рівняння системи:
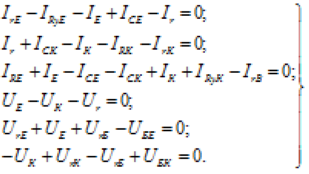
У двох останніх рівняннях 
і 
– величини напруги база - емітер і база - колектор. У систему включаються різницеві апроксимації для похідних 
з кроком h.
Таким чином, математична модель біполярного транзистора є системою рівнянь. Матриця Якобі для цієї системи представлена в таблиці. 1.1 (нульові елементи не позначені).
У цій матриці прийняті наступні позначення коефіцієнтів:
Таблиця 1.1
Матриця Якобі для математичної моделі біполярного транзистора
Приклади до розділу 2. Розв’язання систем лінійних рівнянь
Приклад 2.1: Розв’язати СЛАР методом Гаусса з вибором головного елементу:
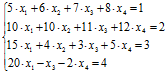
Розв’язок.
Сформуємо матрицю коефіцієнтів A і стовпець B:
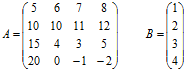
Головний елемент матриці А дорівнює 20. При перестановці рядків отримаємо 
.
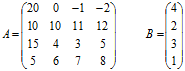
Розрахуємо елементи матриці A1 і стовпця B1:
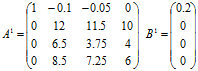
Головний елемент нової матриці 
.
Аналогічно проведемо подальші обчислення:
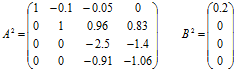
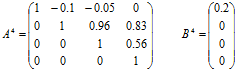
Матриця A4 має трикутний вигляд. Система має єдиний розв’язок. Для його пошуку застосуємо зворотній хід метода Гаусса.
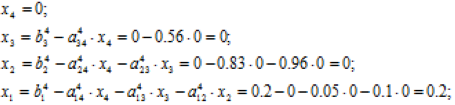
Розв’язок: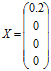 
.
Приклад 2.2: Розв’язати СЛАР з прикладу 2.1 методом Крамера.
Розв’язок.
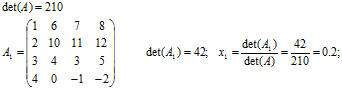
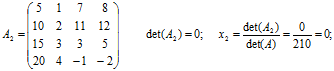
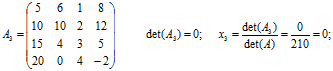
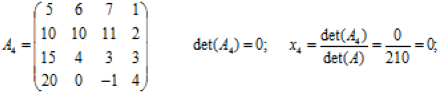
Розв’язок системи X:
.
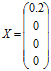