Приклади до розділу 4. Методи розв’язання диференціальних рівнянь

 

Пример 4.1. За методом Ейлера скласти таблицю рішення на відрізку [0;1] для рівняння з початковою умовою y(0) = 1, вибравши крок h = 0,2.

Розв’язок.

Результати обчислень помістимо у таблицю, що заповнюється таким способом:

i	xi	yi	Dyi	Точне у =
0	0	1,0000	0,2000	1,0000
1	0,2	1,2000	0,1733	1,1832
2	0,4	1,3733	0,1561	1,3416
3	0,6	1,5294	0,1492	1,4832
4	0,8	1,6786	0,1451	1,6124
5	1,0	1,8237		1,7320

У першому рядку при i = 0 записується x₀ = 0, y₀ = 1,000 і по них обчислюється f(x₀, y₀) = 1, а потім Dy₀ = hf(x₀, y₀) = 0,2. Тоді за формулою Ейлера одержуємо y₁ = 1 + 0,2 = 1,2.

Значення x₁ = 0,2 і y₁ = 1,2000 записуються у другому рядку при i = 1. Використовуючи їх, можна обчислити

f(x₁,y₁) = 0,8667; Dy₁ = hf(x₁,y₁) = 0,2Ч0,8667 = 0,1733.

Тоді y₂ = y₁ + Dy₁ = 1,2 + 0,1733 = 1,3733.

При i = 2,3,4,5 обчислення ведуться аналогічно. В останньому стовпці таблиці для порівняння поміщені значення точного рішення.

З таблиці видно, що абсолютна похибка для y₅ становить , що становить 5%.

Приклад 4.2. Застосовуючи метод Ейлера, скласти на відрізку [1;1,5] таблицю значень рішення рівняння

с початковими умовами y(1) = 0,77 і y'(1) = –0,44, вибравши крок h = 0,1.

Розв’язок

Замінимо рівняння за допомогою підстановки y' = z, y" =z' системою рівнянь першого порядку

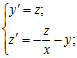
з початковими умовами y(1) = 0,77 і z(1) = –0,44. Таким чином, маємо

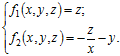
Результати обчислення за формулою Ейлера записані в таблиці

i	xi	yi	DYi	f1i = zi	Dzi
0 1 2 3 4 5	1,0 1,1 1,2 1,3 1,4 1,5	0,77 0,726 0,679 0,629 0,576 0,521	–0,044 –0,047 –0,050 –0,053 –0,055	–0,44 –0,473 –0,503 –0,529 –0,551	–0,033 –0,030 –0,026 –0,022	–0,33 –0,296 –0,260 –0,222

Таблиця заповнюється таким чином. Записуємо в першому рядку i = 0, x₀=1,0; y₀ = 0,77; z₀ = –0,44.

Далі знаходимо

Використовуючи формули Ейлера одержуємо

Таким чином, у другому рядку таблиці ми можемо записати i = 1; x₁ = 1,1; y₁ = 0,726; z₁ = –0,473. За цими значеннями знаходимо

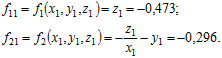
Відповідно

Заповнення таблиці при i =2, 3, 4, 5 здійснюються аналогічно.

Приклади до розділу 6. Методи обробки експериментальних даних

Приклад 6.1. Знайти значення y = f(x) при x = 0,4 заданої таблично:

i	0	1	2	3
xi	0	0,1	0,3	0,5
yi	–0,5	0	0,2	1

Розв’язок.

Квадратична інтерполяція

y=a_ix²+b_ix+c_i

Вибираємо три найближчі крапки до x_t = 0,4

x_i–1 = 0,1;      x_i = 0,3;      x_i+1 = 0,5.

y_i–1 = 0;      y_i = 0,2;      y_i+1 = 1.

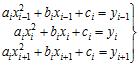     Ю    

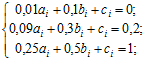
A = ; = ; ==A^–1.

Знайдемо A^–1 = ;

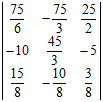= = Ч ;

a = 0 – = 7,5;          b = –2;           c = 0,125;

y = 7,5x² – 2x + 0,125; при x = 0,4; y = 0,525.         

Інтерполяційний многочлен Лагранжа

L(x) = ;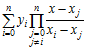

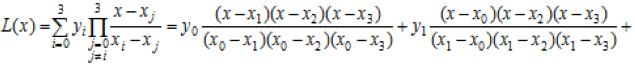
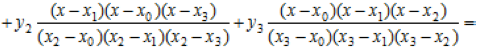
при x = 0,4; y » L(x) = 0,3999.

Інтерполяційний многочлен Ньютона

Маємо випадок нерівностоячих вузлів, n = 3;

Знаходимо роздільні різниці:

f(x₀,x₁) =;

f(x₁,x₂) =;

f(x₂,x₃) = ;

f(x₀,x₁,x₂) =

f(x₁,x₂,x₃) =

f(x₀,x₁,x₂,x₃) =.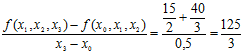

Результати розрахунків помістимо в таблицю:

n	xn	fn	f(xn, xn+1)	f(xn, xn+1, xn+2)	f(xn, xn+1, xn+2, xn+3)
0	0	–0,5
1	0,1	0	5	–40/3	125/3
2	0,3	0,2	1	15/2
3	0,5	1	4

Використовуючи перші в стовпцях розділені різниці, одержимо

N₃(x) = –0,5 + (x – 0)Ч5 + (x – 0)(x – 0,1)(–) + (x – 0)(x – 0,1)(x – 0,3)=

= x³ – 30x² + x – 0,5 .

Нагадаємо, що розрахунки інтерполяційного многочлена Ньютона виконуються по формулі:

,

де      – поточна точка, у якій потрібно обчислити значення многочлена; – розділені різниці порядку k, які обчислюються за такими формулами:

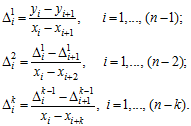
Приклад 6.2. Розглянемо фрагмент таблиці функції

	1,4	1,5	1,7	1,8
	2,38545	2,49749	2,69166	2,77385

Розв’язок.

Запишемо многочлен Лагранжа, використовуючи всю наявну інформацію, тобто покладаючи , у вигляді

    

    

     .

Обчислимо значення в точці , оцінивши спочатку відповідно до формули .

          ,

          ; .

Отже

          .

Скористаємось формою запису інтерполяційного многочлена . Усі обчислення розташуємо в таблиці 1.2.

Таблиця 1.2

		,			,
0	0,2	– 0,1	– 0,3	– 0,4	– 0,012	2,38545	– 993,938
1	0,1	0,1	– 0,2	– 0,3	0,006	2,49749	4162,48
2	– 0,1	0,3	0,2	– 0,1	– 0,006	2,69166	4486,10
3	– 0,2	0,4	0,3	0,1	0,012	2,77385	– 1155,77

          ,

          .

Для порівняння наведемо значення функції для з п’ятьма точними десятковими знаками: .

Приклад 6.3. За допомогою формули Сімпсона обчислити з точністю e = 10^–3.

Розв’язок.

Виберемо крок h.

; x О [a,b], тобто x О [p/4, p/2] ;

< 0,5Ч10^–3.

Обчислимо f ^IV(x)

.         

Оцінимо | f ^IV| на відрізку [p/4, p/2]. Скористаємося величинами і . Вони позитивні та спадають, отже, їх максимальне значення в точці x = p/4.

При цьому +< 81. Таким чином, < 0,5Ч10^–3; h⁴ < 14Ч10^–4; h Ј 0,19.

З іншого боку, для даного методу h вибирається з урахуванням того, щоб [p/4, p/2] ділився на парне число відрізків. Цим двом вимогам відповідає h=p/24 = 0,13 < 0,19, при якому n = = 6. Тоді, щоб похибка округлення не перевищила 0,5Ч10^–3 досить обчислення виконати з 4 знаками після коми.

Складемо таблицю , з h = p/24 = 7° 30? = 0,1309

i	xi0	xi	sin x	y0, y6	y2m	y2m–1
0	45° 00?	0,7854	0,7071	0,9003
1	52° 30?	0,9163	0,7934			0,8659
2	60° 00?	1,0472	0,8660		0,8270
3	67° 30?	1,1781	0,9239			0,7843
4	75° 00?	1,3090	0,9659		0,7379
5	82° 30?	1,4399	0,9914			0,6885
6	90° 00?	1,5708	1,0000	0,6366
Сума				1,5369	1,5649	2,3386

Для n = 6 по формулі Сімпсона

.

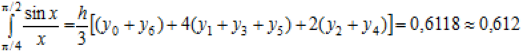Прикла 6.4. По формулі Гаусса при n = 5 обчислити .

Розв’язок.

Зробимо заміну змінної x = 1/2+ t Ч1/2, тоді

.

Складемо таблицю значень підінтегральної функції.

i	xi	f(xi)	qi
1	–0,9061179846	0,24945107	0,236926885
2	–0,538469310	0,23735995	0,478628670
3	0	0,2	0,568888889
4	0,538469310	0,15706211	0,478628670
5	0,906179846	0,13100114	0,236926885

По формулі Гаусса визначимо:

I = 2;

Приклад 10.1. Розглянемо приклад розробки математичної моделі за результатами активного експерименту. Розглядається експеримент з трьома вихідними та трьома вхідними змінними. Вихідні дані для проведення серії експериментів:

Параметр
рівень:	середній	15	50	75
	верхній (1)	20	60	100
	нижній (-1)	10	40	50
інтервал		5	10	25

Результати реалізації активного ПФЕ:

№	Вхідні параметри			Вихідні параметри
досліду
1	1	1	1	1.5	92	6.4
2	-1	1	1	0.5	163	5.5
3	1	-1	1	1	110	4.8
4	-1	-1	1	0.7	142	3.4
5	1	1	-1	1.2	77	6.7
6	-1	1	-1	0.3	152	5.8
7	1	-1	-1	0.4	105	5.1
8	-1	-1	-1	0.3	143	4.0

Після проведення розрахунків за формулами

,

,

отримані такі коефіцієнти регресії:

	0,73	0,28	0,0145	0,019	0,017	0,004	-0,0004
	123	-27	-0,193	0,375	-0,9	0,125	0,0250
	5,19	0,54	0,085	-0,019	-0,008	0,003	0,0003

     Перевірка адекватності моделі: припустимо, що при проведенні паралельних експериментів по кожній комбінації параметрів при середньоквадратичних відхиленнях , , середньоквадратичні відхилення коефіцієнтів регресії становлять, відповідно, ; ; . Тоді , де – критерій Стьюдента, що визначається за статистичними таблицями і залежить від рівня значущості та кількості експериментів . Тоді для можна отримати інтервали довіри відповідно для коефіцієнтів рівняння

     Якщо виключити для кожного з рівнянь коефіцієнти, що менше за ці інтервали, отримаємо остаточні рівняння:

;

;

.

Табличне значення критерію Фішера . Порівняння цього значення із значенням, що розраховано, показує, що . Можна зробити висновок, що ці моделі статистично адекватні.