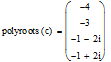Базові операції MathCad

 

Приклад 1. Виконати такі операції:

Приклад 2. Визначити змінні a:=3.4, b:=6.22, (причому змінну c – глобально) та вираз:

Приклад 3. Побудувати декартові (X-Y Plot) і полярні (Polar Plot) графіки наступних функцій:

Розв’язання задач лінійної алгебри в середовищі Mathcad.

До основних функцій лінійної алгебри відносять:

1. Додавання матриць.

2. Віднімання матриць.

3. Множення матриці на скаляр.

4. Множення матриць

5. Транспонування матриці: .

          де ,

6. Знаходження оберненої матриці.

Нехай задана матриця

1. Створення транспонованої матриці в середовищі MathCad:

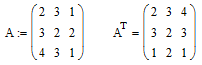
2. Знаходження оберненої матриці:

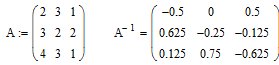
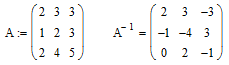
3. Додавання матриць:

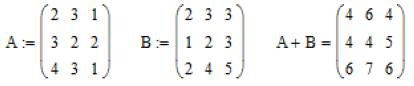
4. Віднімання матриць

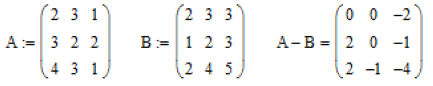
5. Множення матриць:

6. Множення матриці на число:

7. Знаходження детермінанту:

Розв’язання нелінійних рівнянь

     Знаходження коренів нелінійних рівнянь в середовищі MathCad

Для найпростіших рівнянь виду f(x) = 0 рішення в MathСad знаходиться за допомогою функції root:

root( f(х1, x2, ...), х1, a, b )

Повертає значення х1, що належить відрізку [a, b], при якому вираз або функція f(х) пертворюється в 0. Обидва аргументи цієї функції повинні бути скалярами. Функція повертає скаляр.

f(х1, x2, ...) – функція, визначена у робочому документі, або вираз. Вираз повинен повертати скалярні значення.

х1 – ім'я змінної, яка використовується у виразі. Цій змінній перед використанням функції root необхідно присвоїти числове значення. Mathcad використовує його як початкове наближення для пошуку кореня.

Для знаходження коренів виразу, що має вигляд

краще використовувати функцію polyroots, ніж root. На відміну від функції root, функція polyroots не вимагає початкового наближення і повертає відразу всі корені, як дійсні, так і комплексні.

Polyroots(v) – повертає корінь полінома ступеня n. Коефіцієнти полінома знаходяться у векторі v довжиною n+1. Повертає вектор довжини n, що складається з коренів полінома.

v – вектор, що містить коефіцієнти полінома. Вектор v зручно створювати використовую команду Symbolics => Polynomial coefficients.

Приклад 4. Знайти розв’язок нелінійного рівняння . Початкове наближення .

1) Задаємо коефіцієнти рівняння:

2) Задаємо вигляд функції:

3) Задаємо початкове наближення:

4) Знаходимо перший корінь:

5) Знаходимо інші корені:

Відповідь: ,.

Приклад 5. Знайти розв’язок нелінійного рівняння . Початкове наближення .

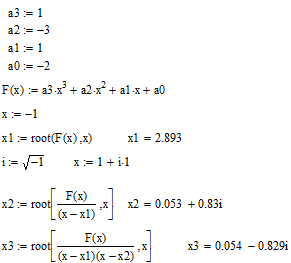
Відповідь:

Коментар: Даний приклад ілюструє, що другий та третій корені даним способом знаходяться з певною похибкою.

Приклад 6. Знайти розв’язок нелінійного рівняння методом Ньютона. Початкове наближення .

Відповідь:

Приклад 7. Знайти розв’язок рівняння

У випадку полінома, можна застосувати функцію polyroots:

Іншим способом отримати розв’язок є символьне рішення за допомогою команди Symbolіc=>Solve for varіable

              

     Розв’язання систем лінійних рівнянь в середовищі MathCad

Систему лінійних рівнянь в середовищі MathCad можна вирішити декількома способами. Найбільш простий з них, з використанням функції lsolve(M, v), де вектор рішення x такий, що M x=v.

Приклад 8. Нехай задана наступна система рівнянь:

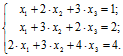
Для розв’язання рівняння в даному середовищі необхідно представити його в матричній формі (матриця лівої частини системи та матриця вільних членів):

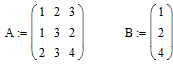
Пошук рішення системи:

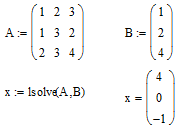
Перевірка знайденого рішення:

.

Відповідь: ; ; .

Іншим способом є розв’язання системи рівнянь за допомогою функцій Given та Find. Для рішення системи рівнянь необхідно виконати такі дії:

  •  Задати початкове наближення для всіх невідомих, що входять у систему рівнянь. Mathcad вирішує систему за допомогою ітераційних методів.
  •  Надрукувати ключове слово Gіven. Воно вказує Mathcad, що далі буде введено систему рівнянь.
  •  Введіть рівняння та нерівності в будь-якому порядку. Використовуйте знак з панелі Boolean або [Ctrl] += .
  •  Введіть функцію Find(z1, z2, . . .), яка повертає точне рішення системи рівнянь. Число аргументів повинно бути рівним числу невідомих.

    Розглянемо розв’язання системи лінійних рівнянь методом ітерацій в середовищі MathCad:

    У Mathcad існують спеціальні функції для обчислення норм матриць:

    normі(A) – повертає невизначену норму матриці А.

    norm1(A) – повертає L1, норму матриці А.

    normе(A) - повертає Евклідову норму матриці А.

    Приклад 10. Розв’яжемо наступну систему:

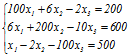
    Приведемо дану систему до вигляду:

    В матричній формі її можна записати так:

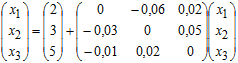
    Перевірка достатньої умови збіжності:

    – визначення початкового наближення рішення

    – визначення кількості ітерацій

    – формула обчислення за методом ітерацій

    Матриця наближених рішень:

    Оцінка похибки:

    Розглянемо рішення системи лінійних рівнянь методом Гауса у середовищі MathCad з використанням наступних функцій:

    rref(A) – повертається ступінчаста форма матриці А.

    augment(A, У) – повертається масив, сформований розташуванням A і В пліч-о-пліч. Масиви A і В повинні мати однакове число рядків.

    submatrіx(A, іr, jr, іc, jc) – повертається субматриця, що складається з всіх елементів з іr по jr і стовпцях з іc по jc.

    Приклад 11. Розв’язати систему рівнянь методом Гаусса.

         Розв’язання задач чисельного інтегрування в середовищі MathCad

    Щоб обчислити визначений інтеграл в середовищі MathCad, потрібно надрукувати його оператор за допомогою панелі Calculus натисканням кнопки зі значком певного інтеграла. З'явиться символ інтеграла з декількома комірками, у які потрібно ввести нижню і верхню межі інтегрування, підінтегральну функцію та змінну інтегрування.

    Інтеграли в середовищі MathCad розв’язуються наступним чином:

    Варіант А:

    Варіант Б:

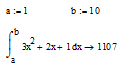
    Варіант В:

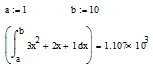
    Приклад 12. Обчислити інтеграл за формулами трапецій, Сімпсона та Гаусса

    Як видно з результатів обчислення, найбільш точне значення отримано за допомогою методу Гаусса.

    Приклад 13. Обчислити інтеграл за методом Монте-Карло при n=10.

    Використана у прикладі функція runif повертає вектор з m випадкових значень, що мають універсальний розподіл на інтервалі [a;b].