
Приклади використання пакету MATLAB для розв’язання чисельних задач
Нелінійні рівняння:
function [k,p,err,P]=fixpt(g,p0,tol,max1)
% Розвязання рівнянь ітераційним методом
% Введення - g - ітераційна фунція, що вводиться як стрічка 'g'
% p0 - початкове наближення
% tol - допустиме відхилення
% max1 - максимальна кількість ітерацій
% Вихід - k - число виконаних ітерацій
% p - наближення для точки
% err - похибка наближення
% P - містить послідовність {pn}
P(1)=p0;
for k=2:max1
P(k)=feval(g,P(k-1));
err=abs(P(k)-P(k-1));
relerr=err/(abs(P(k))+eps);
p=P(k);
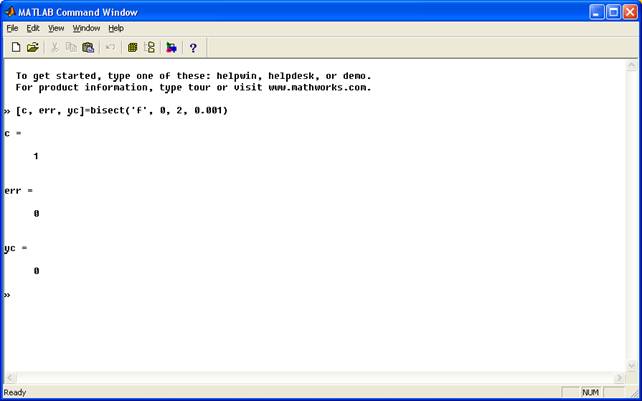
if (err end if k==max1 disp('максимально допустима кількість ітерацій') end P=P'; Щоб запустити програму необхідно у MATLAB Command Window записати [c, err, yc]=bisect(‘f’, a, b, delta), де замість a, b, delta поставити необхідні значення. При цьому файл програми bisect.m та функції f.m повинні знаходитись у папці work папки, де встановлений Matlab. function [c, err, yc]=bisect(f, a, b, delta) % Метод половинного ділення для розв'язання рівнянь % Введення - f - вводиться як строка 'f' % a і b - ліва та права крайні точки % delta - допустиме відхилення % Вихід - с - нуль % yc=f(c) % err - помилка обчислення с ya=feval(f,a); yb=feval(f,b); if ya*yb>0,break,end max1=1+round((log(b-a)-log(delta))/log(2)); for k=1:max1 c=(a+b)/2; yc=feval(f,c); if yc==0 a=c; b=c; elseif yb*yc>0 b=c; yb=yc; else a=c; ya=yc; end if b-a < delta, break, end end c=(a+b)/2; err=abs(b-a); yc=feval(f,c);
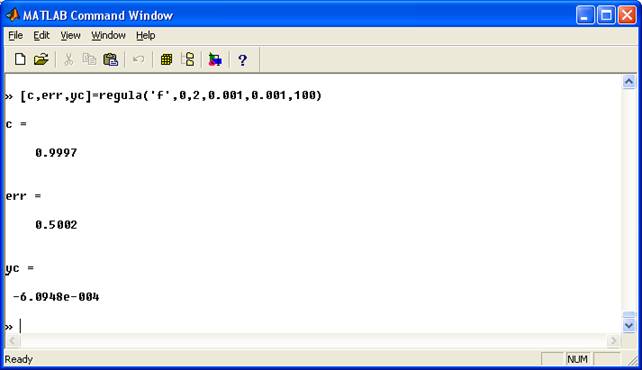
function [c,err,yc]=regula(f,a,b,delta,epsilon,max1) % Метод хорд (хибного положення) для розв'язання рівнянь % Введення - f - функція, що вводиться як стічка 'f' % a и b - ліва та права крайні точки % delta - допустиме відхилення р0 % epsilon - допустиме відхилення для значення функції у % max1 - максимальна кількість ітерацій % Вихід - c - нуль % yc=f(c) % err - похибка обчислення для c ya=feval(f,a); yb=feval(f,b); if ya*yb>0 disp('Зауваження: f(a)*f(b)>0'), break, end for k=1:max1 dx=yb*(b-a)/(yb-ya); c=b-dx; ac=c-a; yc=feval(f,c); if yc==0,break; elseif yb*yc>0 b=c; yb=yc; else a=c; ya=yc; end dx=min(abs(dx),ac); if abs(dx) if abs(yc) end err=abs(b-a)/2; yc=feval(f,c);
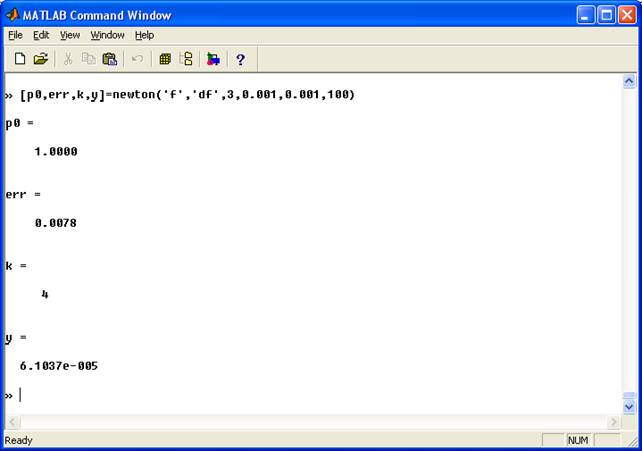
function [p0,err,k,y]=newton(f,df,p0,delta,epsilon,max1) % Метод Нютона для розв'язання рівнянь % Введення - f - функція, що вводиться як стічка 'f' % df - похідна f, що вводиться як стрічка 'df' % p0 - початкове наближення f до нуля % delta - допустиме відхилення р0 % epsilon - допустиме відхилення для значення функції у % max1 - максимальна кількість ітерацій % Вихід p0 - наближення Ньютона до нуля % err - похибка обчислень для p0 % k - кількість ітерацій % y - значення фунції f(p0) for k=1:max1 p1=p0-feval(f,p0)/feval(df,p0); err=abs(p1-p0); relerr=2*err/(abs(p1)+delta); p0=p1; y=feval(f,p0); if (err end
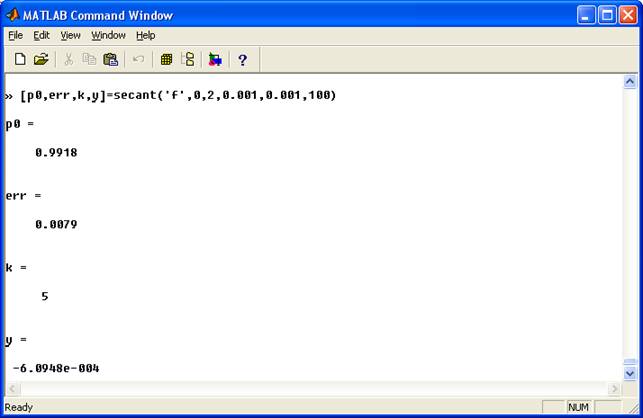
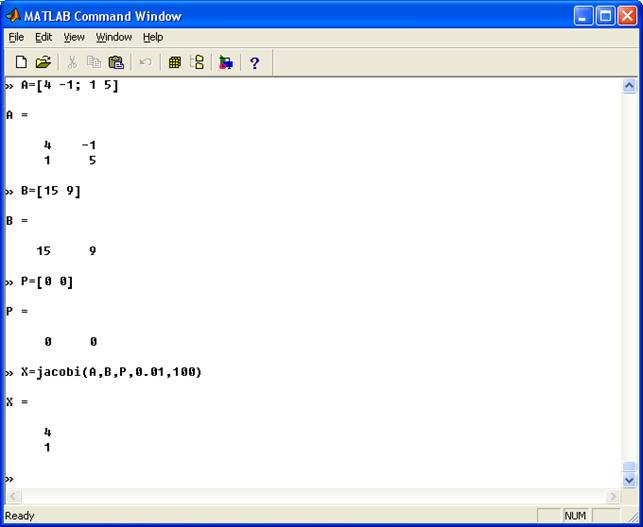
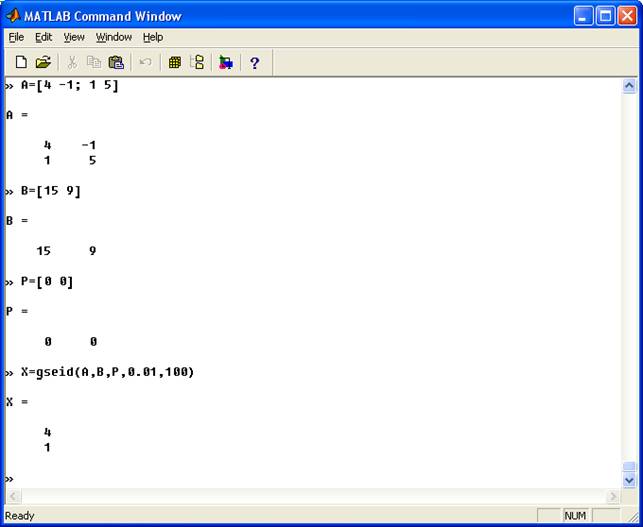
function [p0,err,k,y]=secant(f,p0,p1,delta,epsilon,max1) % Метод січних для розв'язання рівнянь % Введення - f - функція, що вводиться як стічка 'f' % p0 і p1 - початкове наближення f до нуля % delta - допустиме відхилення р1 % epsilon - допустиме відхилення для значення функції у % max1 - максимальна кількість ітерацій % Вихід p1 - наближення до нуля метода січних % err - похибка обчислень для p1 % k - кількість ітерацій % y - значення фунції f(p1) for k=1:max1 p2=p1-feval(f,p1)*(p1-p0)/(feval(f,p1)-feval(f,p0)); err=abs(p1-p2); relerr=2*err/(abs(p2)+delta); p0=p1; p1=p2; y=feval(f,p1); if (err end Системи рівнянь: function X=jacobi(A,B,P,delta,max1) % Розв'язання лінійних рівнянь методом ітерації Якобі % Введення - A - невироджена матриця розміром NxN % B - матриця розміром Nx1 % P - матриця розміром Nx1, початкові наближення % delta - допустиме відхилення для P % max1 - максимальне число відхилень % Вихід - X - матриця розміром Nx1, наближення Якобі до розв'язку % AX=B N=length(B); for k=1:max1 for j=1:N X(j)=(B(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j); end P=X'; end X=X'; function X=gseid(A,B,P,delta,max1) % Розв'язання лінійних рівнянь методом ітерації Якобі % Введення - A - невироджена матриця розміром NxN % B - матриця розміром Nx1 % P - матриця розміром Nx1, початкові наближення % delta - допустиме відхилення для P % max1 - максимальне число відхилень % Вихід - X - матриця розміром Nx1, наближення Якобі до розв'язку % AX=B N=length(B); for k=1:max1 for j=1:N if j==1 X(1)=(B(1)-A(1,2:N)*P(2:N))/A(1,1); elseif j==N X(N)=(B(N)-A(N,1:N-1)*(X(1:N-1))')/A(N,N); else % X містить k-е наближення і P(k-1) X(j)=(B(j)-A(j,1:j-1)*X(1:j-1)-A(j,j+1:N)*P(j+1:N))/A(j,j); end end P=X'; end X=X'; 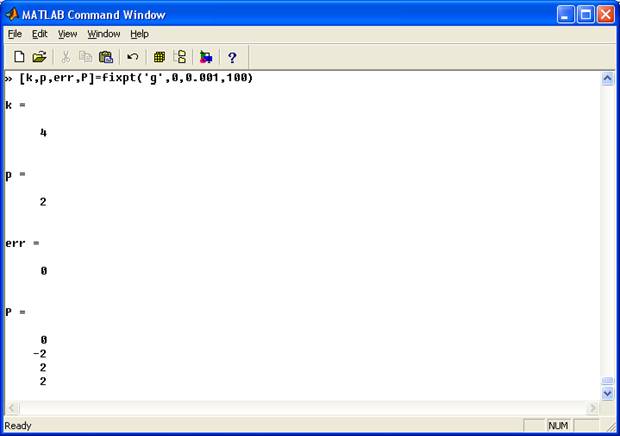
![]()
![]()
![]()