3.1.1 Метод половинного ділення
Нехай дано рівняння f(x)=0. Необхідно знайти його корінь з точністю e на відрізку [a,b], на якому функція безперервна і у кінцях має значення різних знаків, тобто f(a)×f(b)<0. Таким чином, згідно теореми 1, на цьому відрізку існує хоча б один розв’язок рівняння.
Знаходиться середина відрізку [a,b] точка с (рис. 3.2). Корінь може опинитись на відрізку [a,с] або на [с,b], чи співпасти з с. В останньому випадку метод припиняє роботу, інакше за допомогою перевірки виконання умов f(a)×f(c)<0 і f(c)×f(b)<0 з’ясовується, на якій частині відрізку залишився корінь. Далі процедура повторюється для тієї половини відрізку, на якій є корінь, доки відрізок не зменшиться настільки, що його довжина буде менше від заданої похибки.
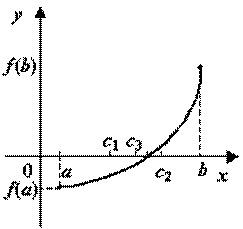
Рисунок 3.2 – Метод половинного ділення
Алгоритм методу:
Крок 1. Знаходиться середина відрізку с:= (b+a)/2.
Крок 2. Перевіряються наступні умови.
1. Якщо f(c)=0 – корінь знайдено.
2. Якщо f(a)×f(c)<0 – корінь на [a,c], тому b:=c.
3. Якщо f(c)×f(b)<0 – корінь на [c,b], тому a:=c.
Крок 3. Перевіряється умова b-a. Якщо вона виконується, то корінь знайдено. В цьому випадку він дорівнює (a+b)/2. Інакше повертаються до кроку 1. Блок-схема методу представлена на рис.3.3.
Похибка розв’язку 
через
n ітерацій знаходиться в межах
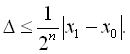
Метод має малу швидкість збіжності, оскільки інтервал, де знаходиться корінь, з кожним кроком зменшується не більше, ніж в два рази.
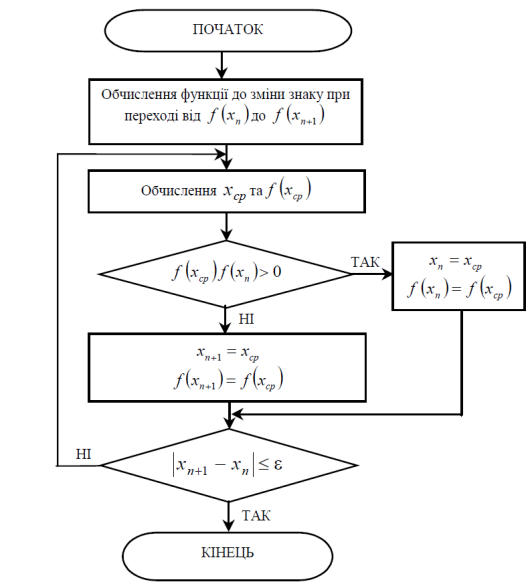
Рисунок 3.3 – Алгоритм методу половинного ділення
3.1.2 Метод хибного положення (хорд)
Нехай дано рівняння f(x)=0. Необхідно знайти його корінь з точністю e на відрізку [a,b], на якому функція безперервна і на кінцях має значення різних знаків, тобто f(a)×f(b)<0. Таким чином, згідно теореми 1, на цьому відрізку існує хоча б один розв’язок рівняння.
Ідея методу хорд полягає в заміні на відрізку [a,b] функції f(x) на пряму, що проходить через кінці її графіка (точки А з координатими (a, f(a)) та В (b, f(b))) (рис.3.4).
Шуканим коренем C буде перетин f(x) з віссю ОХ. Рівняння прямої АВ запишемо у вигляді:
.
Приймаючи у = 0, знаходимо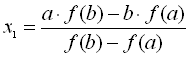 
. Цей вираз можна записати в вигляді:
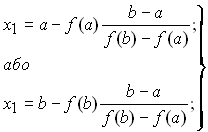(3.1)
Якщо x1 виявляється недостатньо точним, знаходять друге наближення:
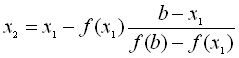. (3.2)
На підставі (3.1) і (3.2) можна записати рекурентну послідовність:
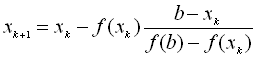, (3.3)
якщо
, і
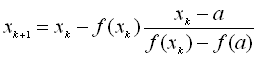(3.4)
якщо
.
Алгоритм методу.
Крок 1. Знаходиться перша точка 
Крок 2. Перевіряються наступні умови.
1. Якщо f(
)=0 – корінь знайдено.
2. Якщо f(a)×f()<0 – корінь на [a, ], тому b:= .
3. Якщо f()×f(b)<0 – корінь на [,b], тому a:= .
Крок 3. Запам’ятовується останнє наближення 
Крок 4. Знаходиться нове наближення
Крок 5. Перевіряються наступні умови.
1. Якщо f()=0 – корінь знайдено.
2. Якщо f(a)×f()<0 – корінь на [a, ], тому b:= .
3. Якщо f()×f(b)<0 – корінь на [,b], тому a:= .
Крок 6. Перевіряється умова 
. Якщо вона виконана, то вважається, що корінь знайдено. В цьому випадку він приймається рівним . Інакше перехід на крок 3.
Похибка розв’язку оцінюється за формулою:
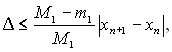
де 
– відповідно, найбільше та найменше значення модуля першої похідної
f(x) на відрізку.
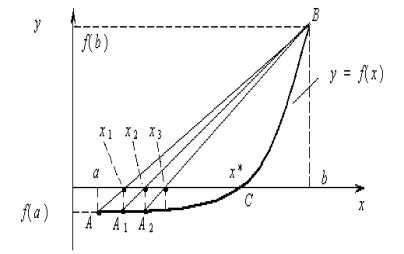
Рисунок 3.4 – Метод хорд
Зауваження. Якщо функція f(x) монотонна та опукла (ввігнута), процес наближення до кореня буде відбуватись завжди з одного боку. Тому після визначення на кроці 2 частини відрізку, на якій є корінь, можна запам’ятати її нерухомий кінець і виключити в циклі перевірку умов на кроці 5.
3.1.3 Метод Ньютона (дотичних)
На відміну від методу хорд, в методі Ньютона функція f(x) замінюється на дотичну і наближення до кореня рівняння визначається точкою перетину дотичної з віссю ОХ.
Рівняння дотичної має вид:
,
де 
– точка, в якій проведена дотична.
З геометричної точки зору xn+1 є значенням абсциси точки перетину дотичної до кривої y=f(x) в точці (xn, f(xn)) з віссю абсцис. Тому метод Ньютона називають також методом дотичних.
Теорема 1. Якщо 
не змінює знака на [a,b], то виходячи з початкового наближення 
, що задовольняє умові 
, можна обчислити методом Ньютона єдиний корінь 
рівняння (1) з будь-яким степенем точності.
Очевидно, що точка перетину дотичної з віссю ОХ, яка визначає перше наближення до кореня, знаходиться по формулі:
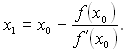
У точці 
проводиться ще одна дотична і знаходиться точка її перетину з віссю ОХ (рис. 3.5).
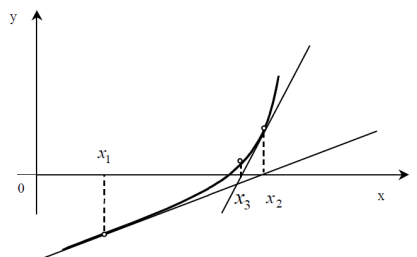
Рисунок 3.5 – Метод Ньютона
Таким чином, наступні наближення розраховуються по формулі:
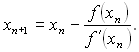
В основі цього методу лежить розкладання функції в ряд Тейлора
Члени, що містять 
у другому і більших степенях, відкидаються і в результаті отримується наведена вище наближена формула для оцінки 
.
Метод завершує роботу тоді, коли відстань між двома останніми точками не стане менше за необхідну точність e.
Для збіжності алгоритму небхідно, щоб функція f(x) була монотонна та опукла (ввігнута) на відрізку [a,b]. Коли в процесі обчислень кут нахилу дотичної 
перетворюється на нуль, застосування цього методу ускладнюється. Можна також показати, що у випадку дуже великих значень 
чи кратних коренів метод Ньютона стає неефективним.
Початкове наближення слід вибирати за формулою:
.
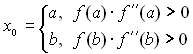Як і в методі хорд, при програмній реалізації методу необхідно запам’ятовувати лише дві останні точки наближення.
Алгоритм методу.
Крок 1. Знаходиться перша точка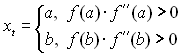 
Крок 2. Запам’ятовується останнє наближення
Крок 3. Знаходиться нове наближення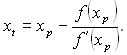 
Крок 4. Перевіряється умова . Якщо вона виконується, то корінь знайдено. В цьому випадку він приймається рівним 
. Інакше перехід на крок 2.
Похибка методу оцінюється як:
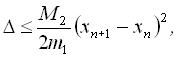
де 
- найбільше за модулем значення другої похідної на інтервалі 
