3.1.4 Метод січних

 

Однією з головних проблем при застосуванні методу Ньютона є необхідність аналітичного опису похідної. Якщо це складно чи неможливо, то можна застосувати її наближену оцінку. Тоді замість методу дотичних застосовується метод січних, за яким

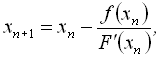
де – наближена оцінка похідної, що розглядається як січна, а не як дотична, і може бути оцінена за формулою

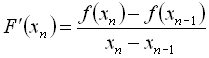
чи

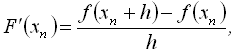
де – деякий невеликий крок.

Алгоритм цього методу подібний методу Ньютона, але з іншою ітераційною формулою.

Геометрична ілюстрація методу наведена на рис. 3.6.

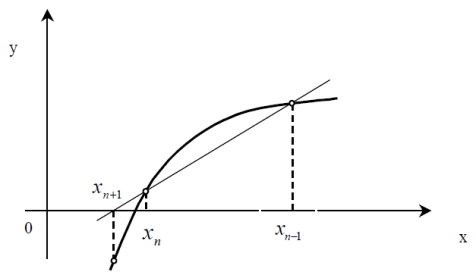
Рисунок 3.6 – Метод січних

 

3.1.5 Метод простої ітерації

 

Метод простої ітерації застосовується до розв’язування нелінійного рівняння виду

.

Вибравши нульове наближення x₀, наступні наближення знаходяться за формулою

               (3.6)

Наведемо достатні умови збіжності методу простої ітерації.

Теорема 2. Нехай для вибраного початкового наближення x₀ на проміжку

функція j(x) задовольняє умові Ліпшиця

               (3.7)

де 0, і виконується нерівність

.

Тоді рівняння має на проміжку S єдиний корінь , до якого збігається послідовність (3.6), причому швидкість збіжності визначається нерівністю

.

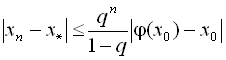Зауваження: якщо функція j(x) має на проміжку S неперервну похідну , яка задовольняє умові

,

то функція j(x) буде задовольняти умові (3.7) теореми 1.

Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:

.

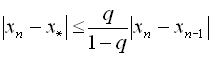Похибка методу на n – ій ітерації

.

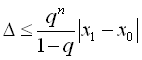Алгоритм методу.    

Крок 1. Знаходиться перша точка ,

Крок 2. Запам’ятовується останнє наближення

Крок 3. Знаходиться нове наближення

Крок 4. Перевіряється умова . Якщо вона виконана, то вважається, що корінь знайдено. В цьому випадку він приймається рівним . Інакше перехід на крок 2.

Геометрична ілюстрація методу наведена на рис. 3.7.

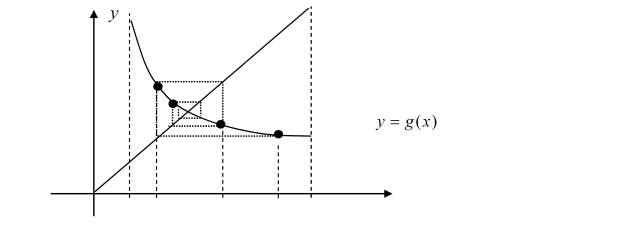
Рисунок 3.7 – Метод простої ітерації для випадку

 

3.1.6 Визначення комплексних коренів

 

Для визначення комплексних коренів (complex roots) можна застосовувати ті ж самі методи, що й для дійсних коренів, але при цьому оперують вже арифметикою комплексних чисел (контроль збіжності та похибки ведеться за модулем комплексного числа), що не завжди зручно для користувача.

Існує низка спеціальних методів, що дозволяють оцінювати комплексні корені, проводячи обчислення з дійсними числами. Більшість з цих методів базується на перетворенні початкового алгебраїчного рівняння (3.1) до добутку квадратичних співмножників типу

,

де – коефіцієнти.

Проміжною формою для здійснення такого перетворення є рівняння у вигляді

,     (3.8)

де - лінійний залишковий член, який прагнуть звести до нуля, і щоб початкове рівняння (3.1) ділилося на квадратичний співмножник без залишку.

Для того, щоб знайти коефіцієнти при припущенні розглянемо систему рівнянь, що виходять з еквівалентності рівнянь (3.1) та (3.2):

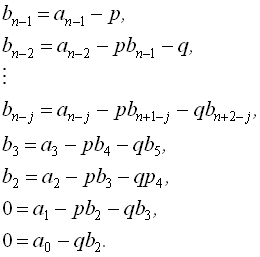          (3.9)

Вона може бути розв’язана методом прогонки чи ітераційним методом Ліна, алгоритм якого представлений на рисунку 3.8.

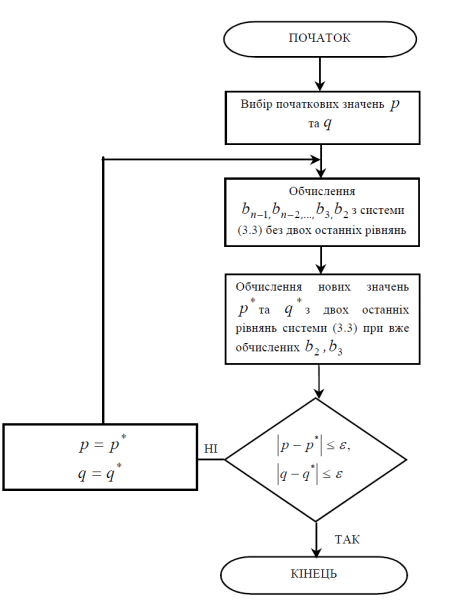
Рисунок 3.8 – Алгоритм методу Ліна