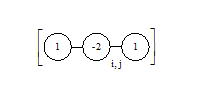Глава 5 Методи розв’язання диференціальних рівнянь в частинних похідних
З розв’язанням диференціальних рівнянь в частинних похідних (differential equations in partial derivatives) інженерам і дослідникам доводиться зустрічатися у багатьох областях науки і техніки, в аеро- і гідродинаміці, ядерній фізиці, радіозв’язку. Математичні моделі з диференціальними рівняннями в частинних похідних широко використовуються в теорії автоматичного керування і у вимірювальній техніці. В таких рівняннях містяться частинні похідні і шукана величина залежить відразу від декількох змінних. Розглянемо диференціальне рівняння другого порядку з двома незалежними змінними:
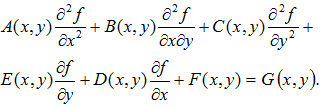 (5.1)
(5.1)
Аналогічно звичайним диференціальним рівнянням єдиний розв’язок рівняння (5.1) можна отримати лише задавши додаткові умови, але оскільки тут присутні дві незалежні змінні ![]() та
та ![]() , умова повинна задаватися для якої-небудь кривої у площині
, умова повинна задаватися для якої-небудь кривої у площині ![]() . Ця умова може бути накладена на функцію
. Ця умова може бути накладена на функцію ![]() або (та) на її похідні та залежати від типу рівняння, яке визначає її вигляд і характер зміни.
або (та) на її похідні та залежати від типу рівняння, яке визначає її вигляд і характер зміни.
Існують три типи диференціальних рівнянь другого порядку:
Рівняння можуть переходити з одного вигляду в інший в залежності від значень коефіцієнтів.
Еліптичні рівняння описують усталені (стаціонарні) процеси, причому задача ставиться в замкненій області і в кожній точці границі цієї області задаються граничні умови. Інші два типи рівнянь описують еволюційні процеси. В таких задачах найбільш поширений випадок, коли на одній частині границі ставлять граничні умови, а на іншій - початкові.
Приклади деяких диференціальних рівнянь в частинних похідних , які описують різні типи задач, наведені в таблиці 5.1.
Таблиця 5.1 Диференціальні рівняння в частинних похідних
В таблиці використані прийняті позначення найбільш поширених операторів:
оператор Лапласа ![]() ;
;
бігармонічний оператор ![]() .
.
Існують два методи розв’язання диференціальних рівнянь в частинних похідних: різницевий метод (метод скінченних різниць) і метод скінченних елементів. В сучасній прикладній математиці обидва методи розглядаються як інтерпретації використання загальної теорії різницевих схем до розв’язання диференціальних рівнянь в частинних похідних .
В основі методу cкінченних елементів лежить варіаційне обчислення. Диференціальне рівняння, яке описує задачу й відповідні граничні умови, використовується для постановки варіаційної задачі. В методі скінченних елементів фізична задача замінюється кусково-гладкою моделлю. Цей метод вимагає складної постановки задачі, високої кваліфікації й досвіду, неуніверсальний (кожне розв’язання застосовується лише для конкретної задачі). Метод скінченних елементів знайшов широке використання для розв’язання спеціальних задач в теоретичній механіці, гідродинаміці, теорії поля, він складний, вимагає серйозної підготовки і знань в конкретній області використання, та для його достатньо повного викладу прийшлося б написати спеціальний підручник. Тому в даній роботі не наводиться докладний виклад методу скінченних елементів, тим більше, що при розв’язанні задач автоматики та систем керування частіше використовується різницевий метод.
5.1 Різницевий метод
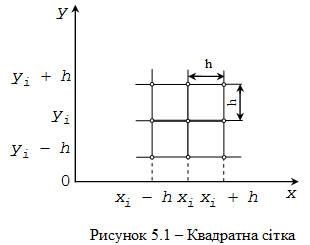
Для диференціальних рівнянь другого порядку в частинних похідних найчастіше використовується двовимірна прямокутна сітка. Центрально - різницеві шаблони, які ![]() застосовують на двовимірній квадратній сітці з кроком
застосовують на двовимірній квадратній сітці з кроком ![]() , зображеній на рисунку 5.1 (індекс
, зображеній на рисунку 5.1 (індекс ![]() надається незалежній змінній
надається незалежній змінній ![]() , а
, а ![]() відноситься до
відноситься до ![]() ), можуть бути отримані аналогічно одновимірному випадку.
), можуть бути отримані аналогічно одновимірному випадку.
Для зручності позначення ![]() замінимо на
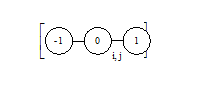
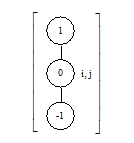
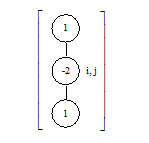
замінимо на ![]() . Користуючись цим позначенням, отримаємо вирази для частинних похідних, з якими доводиться зустрічатися на практиці, й використання яких ілюструється відповідними обчислювальними шаблонами (таблиця 5.2.).
. Користуючись цим позначенням, отримаємо вирази для частинних похідних, з якими доводиться зустрічатися на практиці, й використання яких ілюструється відповідними обчислювальними шаблонами (таблиця 5.2.).
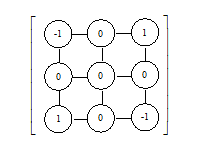
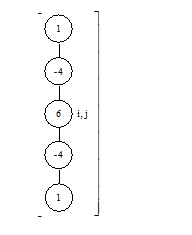
З цих елементів будуються більш складні обчислювальні шаблони для диференціальних рівнянь. Додавання похідних здійснюється суперпозицією відповідних обчислювальних шаблонів. Цим методом конструюються шаблони для ![]() і
і ![]() (рисунок 5.2).
(рисунок 5.2).
Всі наведені обчислювальні шаблони мають похибку другого порядку. Можна побудувати більш точні обчислювальні шаблони, якщо включити у розгляд додаткові вузли. Іноді, щоб звести до мінімуму розповсюдження похибок , користуються лівими або правими різницями.
Таблиця 5.2Обчислювальні шаблони для похідних
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Часто труднощі, які пов’язані з використанням прямокутної сітки, виникають через границю неправильної конфігурації, яка не проходить через вузли сітки. Розглянемо приклад розв’язання такої задачі для обчислювального шаблону рівняння Лапласа в області, що обмежена довільною кривою, яка зображена на рисунок 5.3.
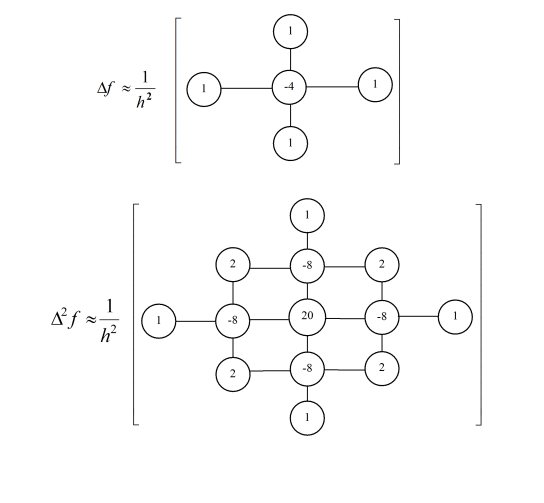
Рисунок 5.2 – Обчислювальні шаблони для операторів
Другі частинні похідні для вузлів, які лежать на границі області, можна записати у вигляді:
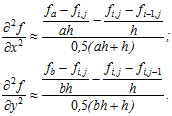
Додавши другі похідні, отримаємо :
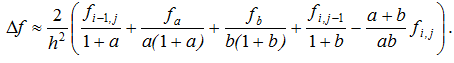 .
.
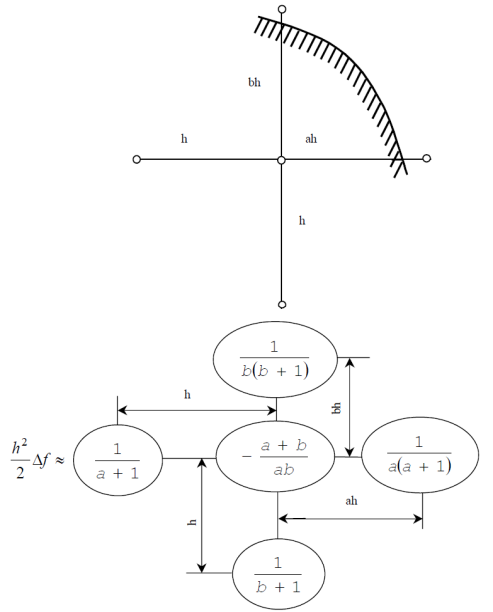
Рисунок 5.3 – Обчислювальний шаблон для границі неправильної форми
Застосувавши обчислювальний шаблон до кожного з n вузлів сітки, отримаємо систему з ![]() рівнянь, яка може були лінійною, якщо початкове диференціальне рівняння має відповідну структуру. В цьому випадку розв’язання задачі зводиться до розв’язання системи рівнянь вигляду:
рівнянь, яка може були лінійною, якщо початкове диференціальне рівняння має відповідну структуру. В цьому випадку розв’язання задачі зводиться до розв’язання системи рівнянь вигляду:
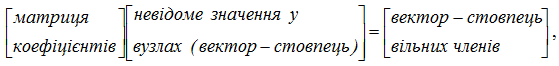 ,
,
яка розв’язується найчастіше ітераційними методами.