4.2     Методи розв’язання крайових задач

 

Методи розв’язання крайових задач розглядаються на прикладі звичайного диференціального рівняння другого порядку

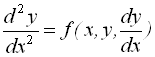
при граничних умовах Методи розв’язання крайових задач розділяють на дві групи: методи, що побудовані на заміні розв’язання крайової задачі розв’язанням декількох задач Коші (методи “стрілянини”) та різницеві методи.

 

4.2.1     Метод “стрілянини”

     Якщо звичайне диференціальне рівняння другого порядку – лінійне, то воно має вигляд:

при

     Крайову задачу можна звести до задачі Коші введенням додаткової початкової умови, крім y(a)=A вводиться y΄(a)=_1.

Знайшовши розв’язок y₁(x), можна поставити іншу початкову умову y΄(a)=₂ і отримати інший розв’язок y₂ (x). Якщо а y₂(b)=β₂, причому β₁ ≠β₂ , то розв’язок:

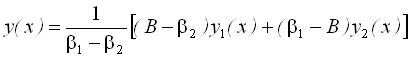
буде задовольняти обидві початкові умови.

     При розв’язуванні нелінійного звичайного диференціального рівняння методами “стрілянини” крайова задача зводиться до розв’язування декількох задач Коші, послідовно вводячи в початкові умови значення :

y(a)=A і y΄(a)=

і намагаючись знайти розв’язок, який задовольняє умову y(b)=B.

     При цьому алгоритм досягнення мети будується на основі одного з методів оптимізації. Однак цей шлях розв’язання задачі пов’язаний з великими обчислювальними труднощами, і тому у випадку нелінійних диференціальних рівнянь перевага надається різницевим методам.

 

4.2.2 Різницеві методи

 

     Апарат різницевих методів (difference methods) являє собою міцний засіб чисельного розв’язування звичайних диференціальних рівнянь і диференціальних рівнянь у частинних похідних. У його основі лежить подання незалежного аргументу на відрізку [a, b] у вигляді дискретної множини точок x_i , i=0,…,n, x₀=a, x_n=b, яка називається сіткою.

     Найбільше поширення отримала рівномірна сітка з кроком x_i-x_i-1=h. При цьому замість безперервної функції f(x) розглядається сіткова функція y_i=f(x_i). Аналогічно проводиться дискретизація функції багатьох змінних, наприклад, двох :

xij , i=0,…,n, j=0,…,m, yij=f(xij).

     Крім найбільш розповсюдженої прямокутної сітки використовують полярну, трикутну, скошену та інші, зображені на рисунку 4.4. Багатовимірні сітки знаходять використання в задачах з частинними похідними по декількох незалежних змінних.

     Розв’язок задачі різницевими методами складається з двох етапів:

-     отримання дискретної (різницевої) апроксимації диференціальних рівнянь і дослідження отриманих при цьому різницевих рівнянь;

-      розв’язання різницевих рівнянь.

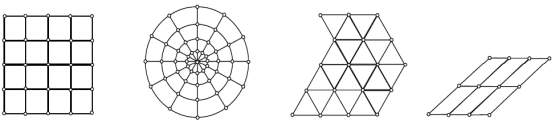
Рисунок 4.5 – Двовимірні сітки

 

При отримані різницевих схем важливу роль відіграє загальна вимога: щоб різницева схема якомога краще наближала основні властивості початкового диференціального рівняння. Такі різницеві схеми можна отримати за допомогою варіаційних принципів та інтегральних співвідношень. Оцінка точності різницевої схеми зводиться до вивчення похибки апроксимації та стійкості. Сіткову функцію можна розглядати як функцію цілочислового аргументу

y(i)=y_i , i= 0, ±1, ±2, … .

Для y_i можна ввести операції, які є дискретним (різницевим) аналогом операцій диференціювання та інтегрування.

Аналогом першої похідної є різниці першого порядку :

– права різниця;

– ліва різниця;

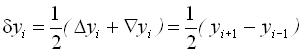– центральна різниця.

Зауважимо, що .

Далі можна записати різниці другого порядку

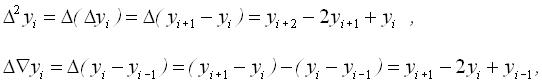
тобто .

Аналогічно визначається різниця m-го порядку:

.

Звідси виходить, що

.

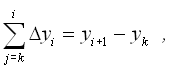
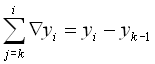На множині вузлів сітки, яка називається шаблоном (тут розглядаються одновимірні шаблони, в наступному розділі вводяться у розгляд двовимірні), замінимо неперервний диференціальний оператор Ly різницевим оператором L_hy .

Наприклад, різницеві оператори для першої похідної на трьох вузлах сітки (x-h, x, x+h):

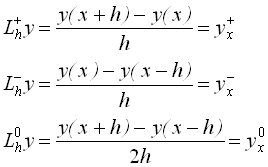
права, ліва і центральна, відповідно, різницеві похідні.

Аналогічно для другої похідної

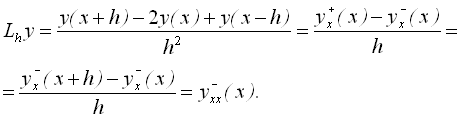
При розв’язуванні крайової задачі записуються різницеві рівняння для всіх n вузлів області змінення x є [a, b]. Враховуючи дві граничні умови y₀=y(a) та y_n=y(b), отримують систему з n-1 алгебраїчних рівнянь з n-1 невідомими y_i . Якщо початкове звичайне диференціальне рівняння лінійне, то задача зводиться до розв’язування системи лінійних алгебраїчних рівнянь, а якщо нелінійне - то нелінійних або трансцендентних алгебраїчних систем. Привести крайову задачу, яку можна розв’язати методом кінцевих різниць, до вигляду, зручного для розробки стандартної програми для ЕОМ складно, оскільки формулювання кожної задачі залежить від вигляду диференціального рівняння, яке розглядають.

В цьому розділі поданий лише короткий опис різницевого підходу без деталізації методів побудови і дослідження різницевих схем. Взагалі різницеві методи є універсальними методами чисельного аналізу, хоча й розглядаються в більшості випадків у зв’язку з розв’язанням крайових задач і диференціальних рівнянь в частинних похідних. Наприклад, метод Ейлера розв’язання задачі Коші може бути інтерпретований як використання одновимірного різницевого оператору. Прикладом узагальненого підходу до розв’язання різноманітних задач обчислювальної математики різницевими методами можуть слугувати праці академіка А. А. Самарського, що містять детальний аналіз і дослідження питань теорії і практики використання різницевих схем.

 

Контрольні запитання та завдання

1.     Сформулюйте задачу Коші і крайову задачу. В чому відмінність у постановці цих задач?

2. Наведіть приклади звичайних диференціальних рівнянь, які розв’язуються лише чисельними методами.

3.     Дайте порівняльну оцінку і визначте області застосування методів розв’язання звичайних диференціальних рівнянь.

4.     Чи можлива крайова задача для рівнянь першого порядку ?

5.     Що таке похибка зрізання (обмеження) ? Чим визначається порядок похибки методу ?

6.     Покажіть, що загальна формула для методу Рунге-Кутта, застосована до рівняння yў=-y з початковою умовою y (0) =1, приводить до співвідношення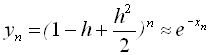

7.     В чому подібність між методами прогнозу і корекції і виправленим методом Ейлера?

8.     Як оцінюються похибки методів Ейлера, Рунге-Кутта, прогнозу і корекції?

9.     Дайте геометричну інтерпретацію методів Ейлера.

10.     Що таке властивість “самостартування” методів розв’язання звичайних диференціальних рівнянь.?    

11.     Як обирається крок при використанні багатокрокових методів розв’язання?

12.     Які рівняння називають “жорсткими”? У чому містяться особливості їх розв’язання?

13.     Для розв’язання яких крайових задач може використовуватись метод “стрілянини”? Як отримати розв’язок крайової задачі з розв’язків декількох задач Коші в цьому методі?

14.     З яких етапів складається розв’язання задачі різницевими методами?

15.     Запишіть всі можливі різницеві оператори для першої і другої похідних.

16.     Як визначаються різницеві оператори для похідних більш високих порядків?