Глава 6     Методи обробки експериментальних даних

 

В цьому розділі розглянуті найбільш важливі задачі обробки даних (інтерполяція, апроксимація, статистична обробка), які зустрічаються в задачах проектування комп’ютеризованих систем управління.

 

6.1 Інтерполяція

 

     Мета інтерполяції (interpolation) – побудувати функцію яка приймає в окремих точках ()(вузли інтерполяції) значення,

          (6.1)

що збігаються з раніше заданими значеннями в цих точках невідомої функції . Геометрично це означає, що потрібно знайти криву певного типу, яка проходить через систему точок (і = 0, 1, 2,..., n) (рисунок 6.1).

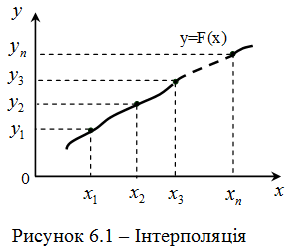
     В загальних випадках ця задача має нескінченну множину розв’язків чи зовсім не має розв’язку, але вона стає однозначною, якщо замість довільної функції шукати поліном ступеня не вище , який задовольняє умову (6.1), тобто

.

     Інтерполяційну формулу , як правило, використовують для наближеного обчислення значень даної функції для (). Така операція називається інтерполяцією. Треба відзначити, що є інтерполяція в вузькому розумінні, коли , та екстраполяція, коли знаходиться за межами інтервалу тобто чи .

Говорячи про процедуру інтерполювання, обов’язково потрібно вказати обмеження, які накладаються на набір базових точок. Початкова сітка точок повинна описувати лише плавну (гладеньку) функцію. Відповідно до умов конкретної задачі обов’язково повинні задаватися значення похідної функції у крайових точках вхідної сітки для отримання однозначного результату.

До основних методів інтерполяції належать:

1) Лінійна інтерполяція (Linear interpolation.). Найбільш простий і швидкий метод, в якому задані вузлові точки з’єднуються прямими.

2) Інтерполяція із застосуванням багаточлена (Interpolation using polynomial). Використовується багаточлен -го порядку, який в загальному випадку має вигляд

де – постійні коефіцієнти. Всі методи знаходження інтерполяційного багаточлена зводяться до отримання постійних коефіцієнтів. До таких методів належать:

a. Інтерполяція різницевими методами.

b. Ермітова поліноміальна інтерполяція.

c. Інтерполяція Лагранжа.

3) Поліноміальна інтерполяція сплайнами (Polynomial spline interpolation). Вузлові точки з’єднуються багаточленами заданого порядку, який обирається в залежності від методу. До найбільш поширених методів інтерполяції сплайнами належать:

a. Класичні кубічні сплайни.

b. Ермітові сплайни.

c. В-сплайни.

d. Криві Без’є.

     Розглянемо декілька методів інтерполяції.

 

6.1.1     Різницеві методи

 

     Існує багато кінцево-різницевих методів інтерполяції. Найбільш поширеним є метод Ньютона для інтерполяції "уперед" (метод Ньютона-Грегорі). Інтерполяційний поліном в цьому випадку має вигляд:

...

...+.

     Коефіцієнти знаходять з рівнянь:

,          ,

які дозволяють записати систему

,

,     (6.2)

……………………………………………………………………

.

     Це лінійна система рівнянь з трикутною матрицею.

     Якщо прийняти крок , то в області змінювання отримаємо одновимірну рівномірну сітку та зможемо скористатись різницевим зображенням системи (6.2), яке приводить до таких різницевих виразів для коефіцієнтів:

,

– права різниця першого порядку в точці ;

,

– права різниця другого порядку;

,

– права різниця j-го порядку.

     Тоді

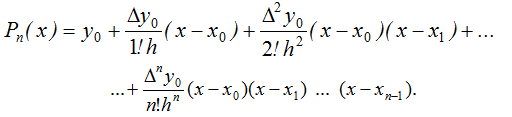(6.3)

 

     З практичної точки зору для визначення різниць вищих порядків використовують вираз:

     При з (6.3) отримуємо формулу для лінійної інтерполяції

а якщо – формулу параболічної чи квадратичної інтерполяції

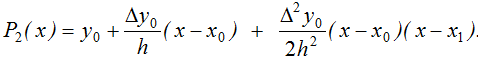
     Якщо дана необмежена кількість значень функції , то кількість може бути будь-якою. Практично в цьому випадку вибирають так, щоб різниця була постійною з заданою точністю. За початкове значення можна приймати будь-яке табличне значення аргументу . Коли кількість значень функції скінчена, то кількість обмежена та не може бути більше кількості значень функції , зменшеної на одиницю.

     Формула (6.3) носить назву першої інтерполяційної формули Ньютона. Цей вираз незручний для інтерполяції поблизу останніх значень . В цьому випадку, як правило, використовують другу інтерполяційну формулу Ньютона, яка отримана при використанні лівих різниць від останнього значення (інтерполяція “назад”). Тоді інтерполяційний поліном має вигляд:

     Коефіцієнти визначаються таким чином:

– ліва різниця першого порядку в точці ,

– ліва різниця другого порядку,

. . . . . .

– ліва різниця j-го порядку.

     Кінцевий вираз для другої інтерполяційної формули Ньютона:

 

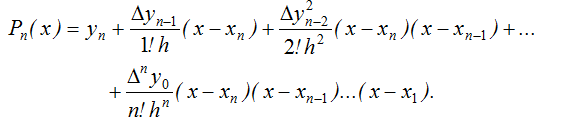
     Інтерполяційні формули Ньютона можуть бути використані для екстраполяції функції. Якщо , то зручно використовувати першу інтерполяційну формулу Ньютона, причому

     Якщо , то використовують другу інтерполяційну формулу Ньютона, де

     Таким чином, перша інтерполяційна формула Ньютона, як правило, використовується для інтерполяції “уперед” та екстраполяції “назад”, а друга – для інтерполяції “назад” та екстраполяції “уперед”.

     В формулах Ньютона використовують ліві та праві різниці. Використання центральних різниць для отримання інтерполяційних формул приводить до формул Гаусса, Стірлінга та Бесселя.

Треба відзначити, що центральні різниці використовуються не в звичайному вигляді, а шляхом застосування правих різниць при поступовому зсуві індексів вліво.

     Ці формули зручно розглядати на () рівновіддалених вузлах інтерполяції

причому

(),

а для функції відомі її значення в цих вузлах .

     Потрібно побудувати поліном ступеня не вище такий, що

     Поліном відшукується у вигляді:

          (6.4)

.

     Аналогічно інтерполяційним формулам Ньютона знаходимо

. . . . . .

     Підставляючи знайдені значення коефіцієнтів в (6.4), отримаємо першу інтерполяційну формулу Гаусса, яка містить різниці (таблиця 6.1):

     Аналогічно можна отримати другу інтерполяційну формулу Гаусса, яка містить центральні різниці:

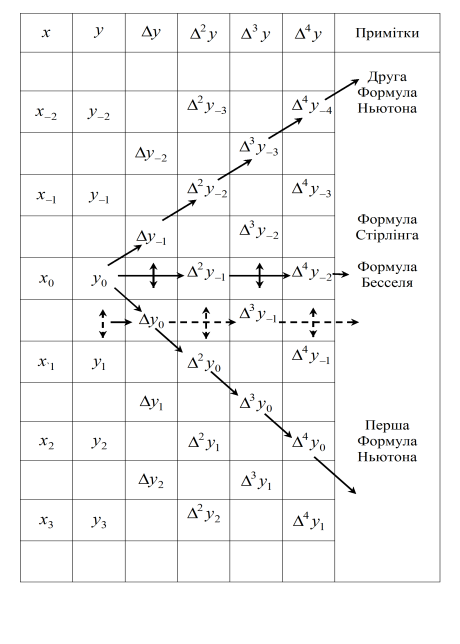
     Використавши середнє арифметичне першої та другої інтерполяційних формул Гаусса, отримаємо формулу Стірлінга. Ці формули дозволяють вивести інтерполяційну формулу Бесселя. Взагалі, використання інтерполяційних формул з центральними різницями доцільно в середині інтервалу, тоді як по його краях, як правило, використовують формули Ньютона. Застосування цих формул розглядається в таблиці 6.1.

     Похибки інтерполяції для формул Ньютона можна оцінити відповідно для першої та другої формул як:

де

     Для формули Стірлінга:

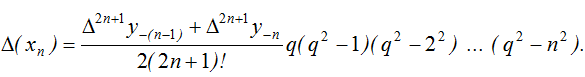
Для випадку нерівновіддалених значень аргументу можна отримати інтерполяційні формули, вживаючи визначення поділених різниць. Наприклад, відношення

називається поділеною різницею першого порядку, а відношення

– поділеною різницею другого порядку.

Застосування різницевих формул інтерполяції

    

Поділені різниці порядку n отримуються з рекурентного відношення:

.

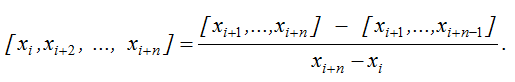     Можна отримати інтерполяційну формулу Ньютона для нерівновіддалених значень аргументу: