6.4  Чисельне інтегрування

 

     В багатьох задачах, що пов’язані з аналізом, ідентифікацією, оцінкою якості різних засобів та систем автоматики та управління, виникає необхідність обчислення певних інтегралів.

     Якщо функція неперервна на відрізку й відома її первісна , то визначений інтеграл від а до в може бути обчислений за формулою Ньютона – Лейбніца

,

де .

Графічно інтеграл визначається площею, що обмежується графіком функції

Але часто точно обчислити інтеграл важко через велику складність аналітичних перетворень, а інколи це взагалі неможливо (в випадках невласних інтегралів), чи коли підінтегральна функція задана набором числових даних, наприклад, отриманих з експерименту.

Задача чисельного інтегрування (numerical integration) функції полягає в обчисленні значення визначеного інтегралу на основі ряду значень підінтегральної функції. Формули чисельного інтегрування часто називають квадратурними.

     Найбільш відомими методами знаходження визначених інтегралів є:

  •  формули прямокутників;
  •  методи Ньютона-Котеса, Гаусса, Чебишева, які основані на використанні так званих квадратурних формул, отриманих заміною інтерполяційними багаточленами;
  • методи Монте-Карло, основані на використанні статистичних моделей.
     

     

    6.4.1 Формули прямокутників

     

    Ідея метода полягає в розбитті відрізку інтегрування на дрібні частини [хi-1,хi] і в побудові прямокутників, які спираються на відрізки [хi-1,хi] й мають висоту . Якщо розбиття відрізку рівномірне, то xi =a+i·h, де h – крок:

    .

    Інтеграл вважається приблизно рівним сумі площ побудованих прямокутників. Узагальнена квадратурна формула прямокутників має вигляд:

    ,

    де точка xiО(xi,xi-1).

    В залежності від вибору xi розрізняють формули лівих, правих й середніх прямокутників.

    Нехай xi =xi-1. , формула лівих прямокутників має вигляд:

    – для нерівновіддалених вузлів,

    – для рівновіддалених вузлів.

    Порядок точності формули – перший, O(h).

    Геометрична інтерпретація наведена на рис. 6.12.

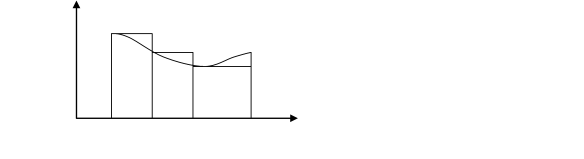
    Рисунок 6.12 – Метод лівих прямокутників

     

    Нехай xi =xi., формула правих прямокутників має вигляд:

    – для нерівновіддалених вузлів,

    – для рівновіддалених вузлів.

    Порядок точності формули – перший, O(h).

    Геометрична інтерпретація наведена на рис. 6.13.

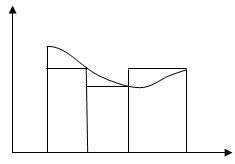
    Рисунок 6.13 – Метод правих прямокутників

     

    Нехай xi =(xi-1+ xi), формула середніх прямокутників має вигляд:

    – для нерівновіддалених вузлів,

     – для рівновіддалених вузлів.

    Порядок точності формул – другий, O(h2).

    Геометрична інтерпретація наведена на рис. 6.14.

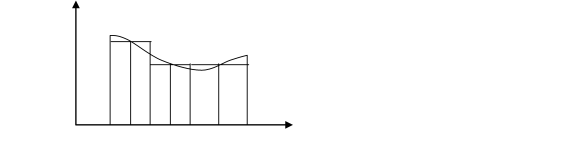
    Рисунок 6.14 – Метод середніх прямокутників

        

    Формули лівих та правих прямокутників можуть бути використані як для аналітично заданих функцій, так і для функцій, заданих таблично. Метод середніх прямокутників може використовуватись для пошуку інтегралів тільки від аналітично заданих функцій.