6.3 Статистична обробка даних
При обробці результатів експериментів в вимірювальній техніці (наприклад, для оцінки похибки вимірювань), автоматиці (розв’язування задач ідентифікації, оптимального управління), статистичній радіотехніці виникає необхідність оцінки характеристик випадкової величини.
В якості оцінки 
невідомого математичного сподівання 
випадкової величини 
використовується середнє арифметичне результатів 
незалежних випробувань
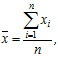
а для оцінки дисперсії 
- співвідношення
.
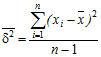При припущенні нормального закону розподілу величини 
можна показати, що величина
має t-розподіл Стьюдента з 
ступенями вільності. Звідси можна визначити надійний інтервал для справжнього значення 
: за відомими значеннями надійної імовірності 
з таблиці 6.3 знаходимо 
, звідки
Таким чином, випадкова величина 
розподілена за нормальним законом з математичним сподіванням 
і дисперсією 
. Справжнє значення 
знаходиться в інтервалі 
з надійною імовірністю 
.
Для оцінки виду закону розподілу найбільше застосування мають критерії Колмогорова і Пірсона, які дозволяють на основі порівняння емпіричної функції розподілу 
, одержаної в вигляді гістограми в результаті обробки експериментальних даних, з гіпотетичною 
, яка відповідає запропонованій гіпотезі, зробити висновки про їх збігання чи незбігання при рівні значущості 
, який визначається як імовірність того, що буде відхилена вірна гіпотеза.
В критерії Колмогорова мірою є величина
,
яку порівнюють з критичним значенням, заданим з таблиці 6.4.
При 
гіпотеза про збігання 
и 
приймається.
В критерії Пірсона обчислюється величина
,
де k – число розрядів гістограми (дискретних значень 
).
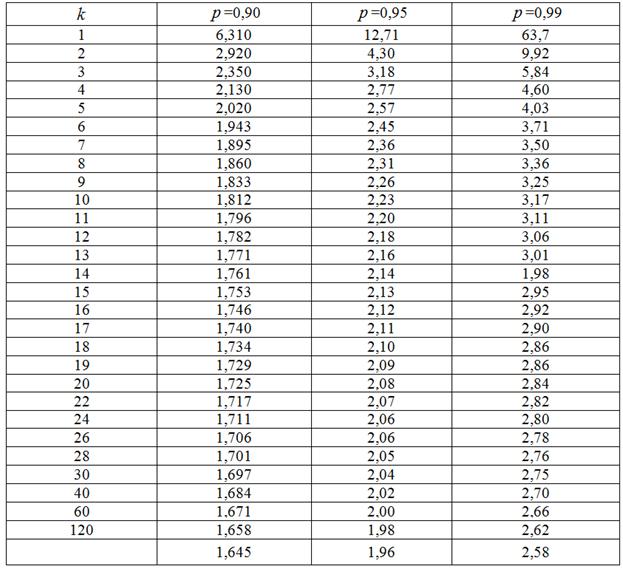
Таблиця 6.3
Значення для надійного інтервалу 
, де величина 
має розподіл Стьюдента в залежності від надійної імовірності 
і числа ступенів вільності 
Таблиця 6.4
Критичні значення 
в залежності від рівня значущості
З таблиці 6.5 визначають критичне значення 
, зважаючи на і число ступенів вільності
,
де 
– число параметрів, що їх містить в собі закон розподілу (для нормального 
=2, пуасонівського 
=1 і т.д.).
При 
гіпотеза приймається.
Таблиця 6.5
Критичні точки розподілу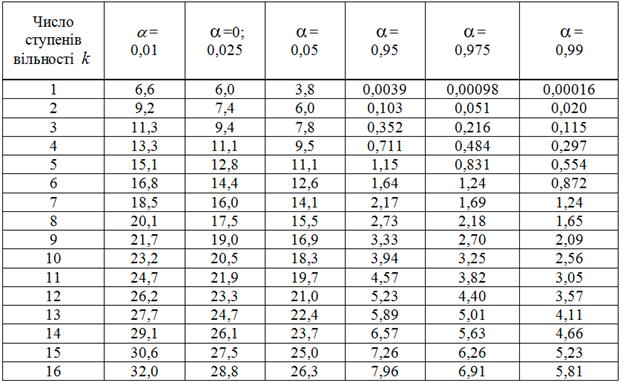
– випадкова величина, яка розподілена за законом 
з ступенями вільності k (таблиця містить значення , що одержані із умови 
)
Якщо порівнюють аналітично одержані закони розподілу ймовірностей, то мірою їх близькості служить значення середньої квадратичної похибки.
Для оцінки взаємозалежності випадкових величин, між якими існує стохастичний зв’язок, використовується коефіцієнт кореляції (correlation coefficient) (n – об’єм вибірки)
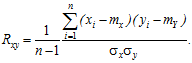
При визначенні взаємозалежності значень випадкових величин в різні моменти часу коефіцієнт кореляції оцінюється за формулою
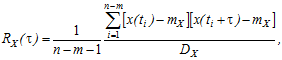
де 
– значення випадкової величини 
в момент часу 
а 
– в момент часу, який відрізняється від 
на інтервал 
. Таким чином, 
– інтервал часу між і та j значеннями 
, 
Інтервал кореляції визначається як відрізок часу, за який кореляційна функція зменшується на 95 %.
Обчислення кореляційної функції за відомими масивами даних 
та 
за допомогою наведених формул не викликає труднощів, а апроксимація виду кореляційної функції типовими кореляційними функціями (таблиця 6.6) може здійснюватися за методом найменших квадратів.
